Cara Menghitung Luas yang Diarsir Panduan Lengkap & Trik Jitu Matematika

Cara menghitung luas yg diarsir – Mari kita mulai petualangan seru ke dunia geometri, di mana kita akan membongkar misteri “cara menghitung luas yang diarsir”. Bayangkan, Anda memiliki sebuah bentuk kompleks, sebagiannya diwarnai atau diarsir, dan Anda ditantang untuk menemukan luas bagian yang tersembunyi itu. Kedengarannya rumit? Jangan khawatir! Kita akan mengubah tantangan ini menjadi permainan yang menyenangkan, penuh dengan trik dan strategi yang mudah dipahami.

Panduan ini akan membawa Anda selangkah demi selangkah, mulai dari pengenalan bangun datar dasar hingga teknik-teknik canggih untuk mengatasi soal-soal rumit. Anda akan belajar mengidentifikasi bentuk-bentuk tersembunyi, menguasai rumus-rumus penting, dan menerapkan konsep-konsep matematika dengan percaya diri. Bersiaplah untuk mengubah pandangan Anda tentang matematika, dari sesuatu yang membosankan menjadi alat yang ampuh untuk memecahkan masalah.

Mengungkap Misteri Bentuk Geometris: Membongkar Rahasia Luas Terarsir

Menghitung luas daerah yang diarsir seringkali menjadi tantangan dalam matematika. Soal-soal ini tidak hanya menguji kemampuan menghitung, tetapi juga kemampuan visualisasi dan pemahaman konsep dasar geometri. Untuk menguasai keterampilan ini, kita perlu memahami berbagai bentuk geometris yang sering muncul dan strategi untuk mengidentifikasinya. Mari kita selami lebih dalam dunia luas terarsir dan buka rahasia di baliknya.

Mengenal Berbagai Bangun Datar yang Sering Muncul

Pemahaman yang kuat tentang bangun datar adalah fondasi utama dalam menyelesaikan soal luas terarsir. Berikut adalah beberapa bangun datar yang paling sering muncul, beserta deskripsi visualnya:

• Persegi: Bentuk persegi memiliki empat sisi yang sama panjang dan empat sudut siku-siku. Bayangkan sebuah kotak sempurna, dengan semua sisinya identik.
• Persegi Panjang: Mirip dengan persegi, tetapi sisi-sisinya tidak harus sama panjang. Visualisasikan sebuah kotak yang memanjang, dengan dua sisi berlawanan memiliki panjang yang sama.
• Segitiga: Bentuk dengan tiga sisi dan tiga sudut. Terdapat berbagai jenis segitiga, seperti segitiga siku-siku (salah satu sudutnya 90 derajat), segitiga sama kaki (dua sisi sama panjang), dan segitiga sama sisi (semua sisi sama panjang).
• Lingkaran: Bentuk melengkung sempurna, dengan semua titik pada garis tepi berjarak sama dari pusat lingkaran. Pikirkan sebuah roda atau koin.
• Jajar Genjang: Bentuk yang memiliki dua pasang sisi sejajar. Visualisasikan sebuah persegi panjang yang “dimiringkan”.
• Trapesium: Bentuk dengan satu pasang sisi sejajar. Bayangkan sebuah atap rumah atau irisan kue.
• Layang-layang: Bentuk dengan dua pasang sisi yang berdekatan sama panjang. Pikirkan layang-layang yang sedang terbang di langit.

Strategi Jitu Mengidentifikasi Bangun Dasar dalam Bentuk Kompleks

Soal luas terarsir seringkali menyajikan bentuk yang lebih kompleks, yang sebenarnya terdiri dari kombinasi beberapa bangun dasar. Kemampuan untuk memecah bentuk kompleks ini menjadi bangun-bangun dasar adalah kunci untuk menyelesaikan soal. Berikut adalah beberapa strategi:

• Visualisasi: Latih kemampuan untuk melihat bentuk-bentuk dasar yang tersembunyi. Putar, balik, atau bagi bentuk kompleks menjadi bagian-bagian yang lebih sederhana.
• Identifikasi Bentuk yang Diketahui: Cari tahu bangun datar apa saja yang membentuk bentuk kompleks tersebut.
• Gunakan Garis Bantu: Tambahkan garis bantu untuk membagi bentuk kompleks menjadi bangun-bangun yang lebih mudah dihitung. Misalnya, tambahkan garis diagonal pada persegi panjang untuk membentuk dua segitiga.
• Perhatikan Simetri: Jika bentuk memiliki simetri, manfaatkan hal ini untuk mempermudah perhitungan.

Contoh Soal:

Sebuah bentuk terdiri dari persegi panjang dengan dua setengah lingkaran di kedua ujungnya. Panjang persegi panjang adalah 10 cm, dan lebarnya 5 cm. Hitung luas daerah yang diarsir.

Penyelesaian:

Memahami cara menghitung luas yang diarsir memang membutuhkan sedikit ketelitian, kan? Kita perlu tahu bentuk dasarnya, lalu mencari selisihnya. Nah, kalau kamu lagi cari inspirasi atau butuh referensi soal matematika, coba deh kunjungi Identif.id. Di sana, kamu bisa menemukan banyak ide dan sumber belajar yang bisa bikin perhitungan luas arsiran jadi lebih mudah dipahami. Jadi, dengan strategi yang tepat, soal luas arsiran bukan lagi momok!

Memahami cara menghitung luas yang diarsir memang membutuhkan ketelitian, mulai dari mengidentifikasi bentuk hingga menerapkan rumus yang tepat. Namun, bagaimana jika kita bisa menyederhanakan proses belajar ini? Nah, Identif hadir sebagai solusi! Dengan platform yang interaktif dan mudah dipahami, Anda bisa lebih cepat menguasai konsep ini. Jadi, setelah memahami dasar-dasarnya, jangan ragu untuk kembali berlatih soal dan mengasah kemampuan Anda dalam menghitung luas yang diarsir.

1. Identifikasi: Bentuk ini terdiri dari persegi panjang dan dua setengah lingkaran (yang jika digabungkan membentuk satu lingkaran penuh).
2. Hitung Luas Persegi Panjang: Luas = panjang x lebar = 10 cm x 5 cm = 50 cm².
3.

Hitung Luas Lingkaran: Diameter lingkaran sama dengan lebar persegi panjang (5 cm), sehingga jari-jari lingkaran adalah 2.5 cm. Luas lingkaran = π x r² = π x (2.5 cm)² ≈ 19.63 cm².
4. Hitung Luas Total: Luas total = Luas persegi panjang + Luas lingkaran ≈ 50 cm² + 19.63 cm² ≈ 69.63 cm².

Rumus-Rumus Dasar Perhitungan Luas Bangun Datar, Cara menghitung luas yg diarsir

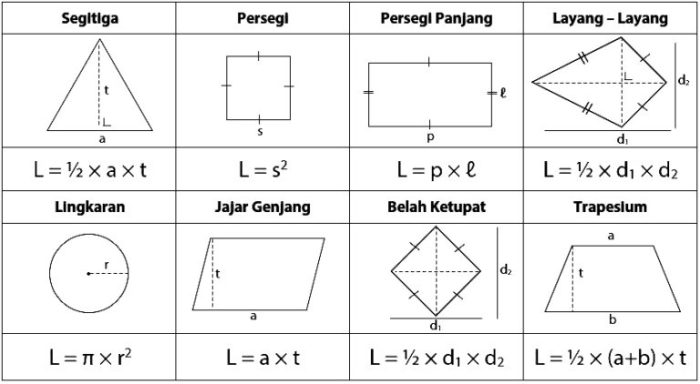
Berikut adalah tabel yang berisi rumus-rumus dasar untuk menghitung luas bangun datar yang sering digunakan:

Bangun Datar	Rumus Luas	Keterangan
Persegi	Sisi x Sisi (s²)	s = panjang sisi
Persegi Panjang	Panjang x Lebar (p x l)	p = panjang, l = lebar
Segitiga	1/2 x Alas x Tinggi (1/2 x a x t)	a = alas, t = tinggi
Lingkaran	π x Jari-jari² (πr²)	π ≈ 3.14 atau 22/7, r = jari-jari
Jajar Genjang	Alas x Tinggi (a x t)	a = alas, t = tinggi
Trapesium	1/2 x (Sisi Sejajar 1 + Sisi Sejajar 2) x Tinggi
Layang-layang	1/2 x Diagonal 1 x Diagonal 2

Tips Praktis Menghindari Kesalahan Umum

Menghitung luas terarsir membutuhkan ketelitian. Berikut adalah beberapa tips untuk menghindari kesalahan umum:

Tips:

• Perhatikan Satuan: Pastikan semua satuan konsisten sebelum melakukan perhitungan. Jika ada satuan yang berbeda, konversikan terlebih dahulu.
• Gunakan Rumus yang Tepat: Pilih rumus yang sesuai dengan jenis bangun datar yang akan dihitung.
• Periksa Kembali Perhitungan: Setelah selesai menghitung, periksa kembali langkah-langkah dan perhitungan untuk memastikan tidak ada kesalahan.
• Hindari Overthinking: Jangan terpaku pada bentuk yang terlalu kompleks. Pecah bentuk menjadi bagian-bagian yang lebih sederhana.

Contoh Kasus:

Seorang siswa menghitung luas lingkaran dengan diameter 10 cm menggunakan rumus luas = π x d². Siswa tersebut salah karena menggunakan diameter (d) dalam rumus. Seharusnya, siswa tersebut menghitung jari-jari (r) terlebih dahulu (r = d/2 = 5 cm), kemudian menggunakan rumus luas = π x r².

Solusi: Selalu perhatikan dengan cermat rumus yang digunakan dan pastikan menggunakan nilai yang benar (jari-jari, bukan diameter untuk lingkaran).

Mengurai Strategi Jitu

Menghitung luas daerah yang diarsir seringkali menjadi momok bagi siswa. Namun, dengan strategi yang tepat, soal-soal ini dapat dipecahkan dengan mudah dan efisien. Artikel ini akan memandu Anda melalui teknik-teknik efektif untuk menaklukkan soal-soal luas terarsir, mulai dari langkah-langkah dasar hingga penerapan konsep matematika yang lebih kompleks. Mari kita bedah strategi jitu untuk menguasai perhitungan luas terarsir!

Rinci Langkah-langkah Sistematis

Memecahkan soal luas terarsir membutuhkan pendekatan yang sistematis. Berikut adalah langkah-langkah yang dapat Anda ikuti:

1. Identifikasi Bentuk Geometris: Langkah pertama adalah mengidentifikasi bentuk-bentuk geometri yang terlibat dalam soal. Apakah itu persegi, lingkaran, segitiga, atau kombinasi dari berbagai bentuk? Perhatikan dengan seksama setiap detail pada gambar.
2. Tentukan Luas Total: Hitung luas total dari bentuk geometri yang lebih besar, yang di dalamnya terdapat daerah yang diarsir. Gunakan rumus yang sesuai dengan bentuk tersebut (misalnya, luas persegi = sisi x sisi, luas lingkaran = πr²).
3. Hitung Luas Bagian yang Tidak Diarsir: Jika ada bagian yang tidak diarsir, hitung juga luasnya. Ini bisa berupa bentuk sederhana atau kombinasi bentuk lainnya.
4. Kurangkan Luas yang Tidak Diarsir: Luas daerah yang diarsir dapat dihitung dengan mengurangi luas bagian yang tidak diarsir dari luas total. Rumusnya adalah: Luas Terarsir = Luas Total – Luas Tidak Diarsir.
5. Periksa Kembali Perhitungan: Setelah mendapatkan jawaban, periksa kembali perhitungan Anda untuk memastikan tidak ada kesalahan.

Contoh Soal dan Penyelesaian:

Sebuah persegi memiliki sisi 10 cm. Di dalamnya terdapat lingkaran dengan diameter yang sama dengan sisi persegi. Hitung luas daerah yang diarsir (daerah di luar lingkaran tetapi di dalam persegi).

1. Identifikasi Bentuk: Persegi dan lingkaran.
2. Luas Total (Persegi): 10 cm x 10 cm = 100 cm².
3. Luas Tidak Diarsir (Lingkaran): Diameter lingkaran = 10 cm, jadi jari-jari = 5 cm. Luas lingkaran = π x 5² ≈ 78.5 cm².
4. Luas Terarsir: 100 cm²
   

   78.5 cm² ≈ 21.5 cm².

Teknik Khusus untuk Bentuk Kompleks

Soal-soal yang melibatkan bentuk kompleks dan kombinasi bangun datar memerlukan teknik khusus. Berikut adalah beberapa teknik yang efektif:

• Pecah Bentuk: Jika bentuknya rumit, pecah menjadi bentuk-bentuk yang lebih sederhana yang luasnya mudah dihitung. Misalnya, membagi bentuk yang tidak beraturan menjadi segitiga, persegi panjang, dan trapesium.
• Gunakan Simetri: Manfaatkan simetri pada gambar untuk mempermudah perhitungan. Jika bentuknya simetris, hitung luas setengah atau seperempat bagian, kemudian kalikan hasilnya.
• Manfaatkan Perbandingan: Jika ada perbandingan antara ukuran sisi atau luas, gunakan perbandingan tersebut untuk menemukan luas yang dicari.
• Perhatikan Sudut: Jika melibatkan sudut, gunakan pengetahuan tentang sudut-sudut khusus (misalnya, sudut 30°, 45°, 60°) dan sifat-sifat segitiga siku-siku untuk mempermudah perhitungan.

Ilustrasi Visual:

Bayangkan sebuah bentuk yang menyerupai rumah. Untuk menghitung luasnya, Anda dapat membaginya menjadi persegi panjang (badan rumah) dan segitiga (atap rumah). Hitung luas masing-masing bagian, kemudian jumlahkan.

Contoh lain, sebuah lingkaran dengan empat lingkaran kecil di dalamnya yang saling bersinggungan. Untuk menghitung luas daerah di luar lingkaran kecil, hitung luas lingkaran besar, kemudian kurangi dengan empat kali luas lingkaran kecil.

Penerapan Konsep Matematika Lanjutan

Beberapa soal luas terarsir memerlukan penggunaan konsep matematika seperti teorema Pythagoras atau trigonometri. Berikut adalah contohnya:

Contoh Soal:

Sebuah segitiga siku-siku memiliki sisi alas 8 cm dan sisi miring 10 cm. Di dalam segitiga tersebut terdapat setengah lingkaran yang menyinggung ketiga sisi segitiga. Hitung luas daerah yang diarsir (daerah di dalam segitiga tetapi di luar setengah lingkaran).

Penyelesaian:

1. Hitung Tinggi Segitiga: Gunakan teorema Pythagoras: a² + b² = c². 8² + b² = 10², sehingga b² = 36, dan b = 6 cm.
2. Hitung Luas Segitiga: Luas = 1/2 x alas x tinggi = 1/2 x 8 cm x 6 cm = 24 cm².
3. Tentukan Jari-jari Setengah Lingkaran: Jari-jari lingkaran dalam segitiga siku-siku dapat dihitung menggunakan rumus: r = (a + b – c) / 2 = (8 + 6 – 10) / 2 = 2 cm.
4. Hitung Luas Setengah Lingkaran: Luas = 1/2 x πr² = 1/2 x π x 2² ≈ 6.28 cm².
5. Hitung Luas Terarsir: Luas Terarsir = Luas Segitiga – Luas Setengah Lingkaran ≈ 24 cm²
   

   6.28 cm² ≈ 17.72 cm².

Tantangan dan Solusi Umum

Siswa seringkali menghadapi tantangan dalam mengerjakan soal luas terarsir. Berikut adalah beberapa tantangan umum dan solusi praktis:

• Kesulitan Mengidentifikasi Bentuk: Solusi: Latih kemampuan visual dengan melihat berbagai jenis soal dan bentuk. Gunakan pensil untuk menandai atau mewarnai bentuk-bentuk yang terlibat.
• Kesulitan Menggunakan Rumus: Solusi: Hafalkan rumus-rumus dasar dan pahami bagaimana rumus tersebut diturunkan. Buat catatan kecil berisi rumus-rumus yang sering digunakan.
• Kesalahan Perhitungan: Solusi: Kerjakan soal dengan teliti dan periksa kembali setiap langkah perhitungan. Gunakan kalkulator jika diperbolehkan, tetapi tetap pahami cara menghitungnya secara manual.
• Kurangnya Pemahaman Konsep: Solusi: Perkuat pemahaman konsep dasar geometri, teorema Pythagoras, dan trigonometri. Kerjakan soal-soal latihan dari tingkat kesulitan yang mudah hingga sulit.

Membedah Variasi Soal

Memahami konsep luas terarsir adalah kunci untuk menguasai geometri. Namun, tantangan sebenarnya terletak pada kemampuan untuk mengaplikasikan konsep ini dalam berbagai variasi soal. Ujian dan tes seringkali menyajikan soal dengan tingkat kesulitan yang berbeda-beda, mulai dari yang sederhana hingga yang membutuhkan pemikiran analitis yang mendalam. Artikel ini akan membahas secara mendalam berbagai tipe soal luas terarsir yang umum ditemui, memberikan contoh soal, serta strategi untuk menyelesaikannya dengan efektif.

Kemampuan untuk mengidentifikasi bentuk-bentuk geometri yang terlibat, memahami hubungan antar luas, dan menerapkan rumus yang tepat adalah keterampilan yang sangat penting. Mari kita bedah beberapa variasi soal yang sering muncul.

Soal Sederhana: Menghitung Luas Terarsir dari Bentuk Dasar

Soal tipe ini biasanya melibatkan bentuk-bentuk geometri dasar seperti persegi, persegi panjang, segitiga, dan lingkaran. Soal-soal ini bertujuan untuk menguji pemahaman dasar tentang rumus luas dan kemampuan untuk mengidentifikasi bagian mana yang perlu dihitung.

Contoh Soal:

Sebuah persegi panjang berukuran panjang 10 cm dan lebar 6 cm. Di dalam persegi panjang tersebut terdapat sebuah lingkaran dengan diameter 6 cm. Hitunglah luas daerah yang diarsir (daerah di dalam persegi panjang tetapi di luar lingkaran).

Pembahasan:

1. Hitung luas persegi panjang: Luas = panjang x lebar = 10 cm x 6 cm = 60 cm².
2. Hitung luas lingkaran: Jari-jari lingkaran = diameter / 2 = 6 cm / 2 = 3 cm. Luas = πr² = π x (3 cm)² ≈ 28.26 cm². (Gunakan π ≈ 3.14)
3. Hitung luas daerah yang diarsir: Luas = Luas persegi panjang – Luas lingkaran = 60 cm²
   

   28.26 cm² ≈ 31.74 cm².

Soal ini menguji kemampuan untuk menerapkan rumus luas persegi panjang dan lingkaran, serta melakukan pengurangan sederhana.

Soal dengan Konsep Perbandingan dan Proporsi

Soal jenis ini melibatkan konsep perbandingan dan proporsi, yang seringkali mengharuskan kita untuk menghitung luas berdasarkan perbandingan panjang sisi atau luas bagian-bagian tertentu. Memahami konsep kesebangunan dan kekongruenan sangat penting dalam menyelesaikan soal-soal ini.

Contoh Soal:

Sebuah segitiga ABC memiliki luas 24 cm². Titik D terletak pada sisi AB sehingga AD:DB = 1:2. Garis DE sejajar dengan BC, dan E terletak pada sisi AC. Hitunglah luas segitiga ADE.

Oke, mari kita bedah cara menghitung luas yang diarsir! Konsep dasarnya sederhana: identifikasi bentuk, hitung luas total, lalu kurangi area yang tidak diarsir. Tapi, bagaimana jika kamu ingin menghitung sesuatu yang lebih konkret, seperti peluang karir? Nah, bagi kamu yang berdomisili di Mandailing Natal, jangan lewatkan Lowongan Kerja Teller Bank BRI Di Kabupaten Mandailing Natal Tahun 2025 (Resmi).

Ini bisa jadi langkah awal yang tepat! Setelah mendapatkan pekerjaan impian, jangan lupa, keahlian menghitung luas tetap berguna, misalnya untuk mengukur luas area yang akan kamu tempati.

Pembahasan:

1. Karena DE sejajar dengan BC, maka segitiga ADE sebangun dengan segitiga ABC.
2. Perbandingan sisi AD:AB = 1:(1+2) = 1:3.
3. Perbandingan luas segitiga yang sebangun adalah kuadrat dari perbandingan sisinya. Jadi, Luas ADE : Luas ABC = (AD/AB)² = (1/3)².
4. Luas ADE = (1/9) x Luas ABC = (1/9) x 24 cm² ≈ 2.67 cm².

Soal ini membutuhkan pemahaman tentang sifat-sifat segitiga sebangun dan bagaimana perbandingan sisi memengaruhi perbandingan luas.

Tabel Contoh Soal dan Pembahasan

Berikut adalah tabel yang memuat contoh soal dengan berbagai tingkat kesulitan, beserta kunci jawaban dan penjelasan singkatnya:

No.	Tingkat Kesulitan	Soal	Kunci Jawaban	Penjelasan Singkat
1	Mudah	Hitunglah luas daerah yang diarsir pada persegi dengan sisi 8 cm, jika di dalamnya terdapat lingkaran dengan diameter 4 cm.	48.56 cm²	Hitung luas persegi, lalu kurangi dengan luas lingkaran.
2	Sedang	Sebuah persegi panjang berukuran 12 cm x 8 cm. Di dalamnya terdapat dua buah lingkaran identik yang saling bersinggungan. Hitung luas daerah yang tidak tertutupi lingkaran.	40.96 cm²	Hitung luas persegi panjang, lalu kurangi dengan dua kali luas lingkaran.
3	Sulit	Pada segitiga siku-siku dengan sisi alas 6 cm dan tinggi 8 cm, dibuat persegi di dalamnya. Hitung luas persegi tersebut.	5.76 cm²	Gunakan konsep kesebangunan untuk menemukan panjang sisi persegi.
4	Sangat Sulit	Dua lingkaran identik dengan jari-jari 5 cm bersinggungan. Sebuah persegi panjang menyinggung kedua lingkaran tersebut. Jika panjang persegi panjang 20 cm, hitung luas daerah yang diarsir di luar lingkaran tetapi di dalam persegi panjang.	21.5 cm²	Hitung luas persegi panjang, kurangi dengan luas dua lingkaran.

Tips Mengelola Waktu

Mengelola waktu dengan efektif adalah kunci sukses dalam mengerjakan soal-soal perhitungan luas terarsir, terutama dalam ujian atau tes yang dibatasi waktu.

• Pahami Soal dengan Cermat: Baca soal dengan teliti untuk memahami apa yang ditanyakan dan bentuk-bentuk geometri yang terlibat.
• Buat Sketsa: Buat sketsa sederhana untuk memvisualisasikan soal. Ini akan membantu Anda memahami hubungan antar bentuk dan memudahkan perhitungan.
• Prioritaskan Soal yang Mudah: Kerjakan soal yang Anda kuasai terlebih dahulu. Ini akan membantu Anda membangun kepercayaan diri dan menghemat waktu.
• Gunakan Rumus dengan Cepat: Hafalkan rumus-rumus luas yang umum.
• Periksa Kembali Jawaban: Jika waktu memungkinkan, periksa kembali jawaban Anda untuk memastikan tidak ada kesalahan perhitungan.

Merangkai Solusi Cerdas: Aplikasi Praktis Perhitungan Luas Terarsir

Perhitungan luas terarsir bukan hanya sekadar latihan di buku pelajaran. Konsep ini memiliki aplikasi yang luas dan relevan dalam berbagai aspek kehidupan sehari-hari, dari perencanaan konstruksi hingga desain interior. Memahami bagaimana menerapkan perhitungan ini memungkinkan kita untuk memecahkan masalah praktis, meningkatkan efisiensi, dan membuat keputusan yang lebih baik. Mari kita telusuri bagaimana konsep ini diterapkan dalam dunia nyata.

Dalam bagian ini, kita akan melihat bagaimana perhitungan luas terarsir digunakan dalam berbagai bidang, memberikan contoh konkret, dan memberikan sumber daya tambahan untuk memperdalam pemahaman Anda.

Aplikasi Praktis Perhitungan Luas Terarsir dalam Kehidupan Nyata

Konsep perhitungan luas terarsir memiliki peran penting dalam berbagai bidang. Penerapannya membantu dalam pengambilan keputusan yang lebih baik, efisiensi penggunaan sumber daya, dan perencanaan yang lebih akurat. Berikut adalah beberapa contoh nyata:

• Arsitektur dan Konstruksi: Dalam arsitektur, perhitungan luas terarsir digunakan untuk menentukan luas permukaan yang akan dicat, dilapisi, atau ditutupi dengan material tertentu. Misalnya, seorang arsitek perlu menghitung luas dinding yang akan dilapisi dengan ubin atau wallpaper. Perhitungan ini juga krusial dalam estimasi biaya material dan tenaga kerja. Di bidang konstruksi, perhitungan ini digunakan untuk menentukan volume beton yang dibutuhkan untuk fondasi atau luas lahan yang akan dibangun.

• Desain Interior: Desainer interior menggunakan perhitungan luas terarsir untuk merancang tata letak ruangan yang efisien dan estetis. Mereka dapat menghitung luas lantai yang akan ditutupi karpet, luas dinding yang akan dihias dengan dekorasi, atau luas area yang akan ditempati oleh furnitur. Perhitungan ini membantu dalam perencanaan ruang yang optimal dan memastikan bahwa semua elemen desain saling melengkapi.
• Desain Lanskap: Dalam desain lanskap, perhitungan luas terarsir digunakan untuk menentukan luas area yang akan ditanami rumput, bunga, atau pohon. Hal ini membantu dalam perencanaan irigasi, penentuan jumlah tanaman yang dibutuhkan, dan estimasi biaya penanaman. Perhitungan ini juga penting untuk menentukan luas area yang akan digunakan untuk jalur setapak, kolam, atau elemen lanskap lainnya.
• Manufaktur: Di bidang manufaktur, perhitungan luas terarsir digunakan untuk mengoptimalkan penggunaan material. Misalnya, seorang insinyur perlu menghitung luas material yang dibutuhkan untuk memotong komponen dari lembaran logam atau plastik. Perhitungan ini membantu mengurangi limbah material dan meningkatkan efisiensi produksi.
• Perencanaan Kota: Perhitungan luas terarsir juga diterapkan dalam perencanaan kota untuk menghitung luas lahan yang digunakan untuk berbagai tujuan, seperti perumahan, komersial, atau ruang publik. Perhitungan ini membantu dalam perencanaan infrastruktur, penentuan kapasitas jalan, dan evaluasi dampak lingkungan.

Menyelesaikan Masalah Praktis dengan Perhitungan Luas Terarsir

Perhitungan luas terarsir tidak hanya relevan dalam perencanaan, tetapi juga dalam memecahkan masalah praktis sehari-hari. Kemampuan ini memungkinkan kita untuk membuat keputusan yang lebih tepat dan efisien.

• Menghitung Luas Lahan: Bayangkan Anda memiliki sebidang tanah dengan bentuk yang tidak beraturan. Dengan membagi bidang tersebut menjadi bentuk-bentuk geometris yang lebih sederhana (seperti persegi panjang, segitiga, atau trapesium), Anda dapat menghitung luas masing-masing bentuk dan menjumlahkannya untuk mendapatkan luas total lahan. Hal ini sangat berguna dalam perencanaan pertanian, pembangunan rumah, atau investasi properti.
• Mengevaluasi Efisiensi Penggunaan Material: Dalam proyek konstruksi, perhitungan luas terarsir dapat digunakan untuk mengevaluasi efisiensi penggunaan material. Misalnya, jika Anda memiliki lembaran material tertentu, Anda dapat menghitung luas bagian yang digunakan dan membandingkannya dengan luas total lembaran untuk menentukan persentase penggunaan material. Hal ini membantu mengurangi limbah dan mengoptimalkan biaya.
• Merancang Tata Letak Ruangan: Dalam desain interior, perhitungan luas terarsir memungkinkan Anda untuk merancang tata letak ruangan yang optimal. Anda dapat menghitung luas area yang akan ditempati oleh furnitur, mempertimbangkan sirkulasi ruang, dan memastikan bahwa ruangan tersebut berfungsi dengan baik dan estetis.
• Menentukan Volume: Dalam kasus tiga dimensi, perhitungan luas terarsir menjadi dasar untuk menghitung volume. Misalnya, untuk menghitung volume sebuah kolam renang, Anda perlu menghitung luas permukaan kolam (yang merupakan luas terarsir) dan mengalikannya dengan kedalaman kolam.

Sumber Belajar Tambahan

Untuk memperdalam pemahaman Anda tentang perhitungan luas terarsir, berikut adalah beberapa sumber belajar tambahan yang bermanfaat:

• Buku Teks Matematika: Buku teks matematika sekolah menengah atau perguruan tinggi seringkali menyertakan bab tentang geometri dan perhitungan luas.
• Website Pendidikan: Banyak website pendidikan menyediakan materi pembelajaran gratis tentang matematika, termasuk perhitungan luas. Contohnya adalah Khan Academy, Math is Fun, dan Ruangguru.
• Video Tutorial: Platform seperti YouTube menyediakan berbagai video tutorial yang menjelaskan konsep perhitungan luas terarsir dengan cara yang mudah dipahami.
• Aplikasi Pembelajaran Matematika: Terdapat aplikasi seluler yang dirancang untuk membantu siswa belajar matematika, termasuk perhitungan luas, melalui latihan interaktif dan contoh soal.

Contoh Soal dan Penyelesaian

Berikut adalah contoh soal yang mengintegrasikan konsep perhitungan luas terarsir dengan konsep matematika lainnya, beserta penyelesaiannya:

Soal: Sebuah taman berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Di tengah taman terdapat kolam berbentuk lingkaran dengan diameter 4 meter. Berapakah luas area taman yang tidak tertutupi oleh kolam?

Penyelesaian:

1. Hitung Luas Taman: Luas persegi panjang = panjang x lebar = 12 m x 8 m = 96 m².
2. Hitung Luas Kolam: Jari-jari kolam = diameter / 2 = 4 m / 2 = 2 m. Luas lingkaran = π x r² = π x (2 m)² ≈ 12.56 m² (dengan π ≈ 3.14).
3. Hitung Luas Area Taman yang Tidak Tertutupi Kolam: Luas area = Luas Taman – Luas Kolam = 96 m²
   

   12.56 m² ≈ 83.44 m².

Kesimpulan: Luas area taman yang tidak tertutupi oleh kolam adalah sekitar 83.44 meter persegi.

Contoh Soal Lain: Sebuah ruangan berbentuk persegi panjang berukuran 5 meter x 4 meter. Di dalam ruangan tersebut terdapat karpet berbentuk persegi panjang yang berukuran 3 meter x 2 meter. Hitunglah luas lantai ruangan yang tidak tertutupi karpet.

Penyelesaian:

1. Hitung Luas Ruangan: Luas persegi panjang = panjang x lebar = 5 m x 4 m = 20 m².
2. Hitung Luas Karpet: Luas persegi panjang = panjang x lebar = 3 m x 2 m = 6 m².
3. Hitung Luas Lantai yang Tidak Tertutupi Karpet: Luas area = Luas Ruangan – Luas Karpet = 20 m²
   

   6 m² = 14 m².

Kesimpulan: Luas lantai ruangan yang tidak tertutupi karpet adalah 14 meter persegi.

Membangun Pemahaman Konseptual

Memahami konsep dasar dalam perhitungan luas terarsir adalah fondasi penting untuk menguasai topik ini. Daripada hanya menghafal rumus, pendekatan konseptual memungkinkan siswa untuk beradaptasi dengan berbagai jenis soal dan mengembangkan kemampuan berpikir kritis. Pemahaman yang kuat akan konsep juga membuka pintu ke pemahaman yang lebih dalam tentang matematika secara keseluruhan.

Mari kita selami lebih dalam tentang bagaimana kita dapat membangun pemahaman konseptual yang kokoh.

Pentingnya Pemahaman Konsep Dasar

Pemahaman konsep dasar luas terarsir jauh lebih berharga daripada sekadar menghafal rumus. Menguasai konsep memungkinkan siswa untuk memecahkan soal-soal yang bervariasi dan kompleks, bahkan yang belum pernah mereka lihat sebelumnya. Sebagai contoh, bayangkan siswa yang hanya menghafal rumus luas lingkaran. Mereka mungkin kesulitan jika dihadapkan pada soal yang melibatkan luas terarsir dari seperempat lingkaran yang dipotong oleh sebuah segitiga. Namun, siswa yang memahami konsep luas sebagai ukuran ruang yang ditempati oleh suatu bentuk, serta bagaimana bentuk-bentuk tersebut berinteraksi, akan mampu memecahkan soal tersebut dengan lebih mudah.

Mereka akan memahami bahwa mereka perlu menghitung luas seperempat lingkaran dan kemudian mengurangi luas segitiga.

Pendekatan konseptual juga memfasilitasi transfer pengetahuan ke konsep matematika lainnya. Misalnya, pemahaman tentang luas terarsir dapat membantu dalam memahami konsep integral dalam kalkulus. Ketika kita menghitung luas di bawah kurva, kita sebenarnya menggunakan konsep yang sama dengan perhitungan luas terarsir, yaitu membagi area menjadi bagian-bagian kecil dan menjumlahkannya.

Hubungan Luas Terarsir dengan Konsep Matematika Lainnya

Konsep luas terarsir memiliki hubungan erat dengan berbagai konsep matematika lainnya. Salah satu hubungan yang paling jelas adalah dengan konsep integral dalam kalkulus. Dalam kalkulus, integral digunakan untuk menghitung luas di bawah kurva. Konsep ini pada dasarnya sama dengan menghitung luas terarsir. Perbedaannya terletak pada tingkat kompleksitas dan formalitas.

Dalam perhitungan luas terarsir sederhana, kita seringkali menggunakan rumus-rumus geometri dasar. Dalam kalkulus, kita menggunakan integral untuk menghitung luas di bawah kurva yang lebih kompleks, yang tidak dapat dihitung dengan rumus geometri dasar.

Selain itu, konsep luas terarsir juga berhubungan dengan konsep turunan. Turunan digunakan untuk menentukan laju perubahan suatu fungsi. Dalam konteks geometri, turunan dapat digunakan untuk menentukan gradien garis singgung pada suatu kurva. Konsep ini dapat digunakan untuk membantu menghitung luas terarsir yang dibatasi oleh kurva dan garis singgung.

Berikut adalah contoh ilustrasi deskriptif yang menggambarkan hubungan antara luas terarsir dan konsep matematika lainnya:

Bayangkan sebuah persegi panjang. Luas persegi panjang ini dapat dihitung dengan mengalikan panjang dan lebarnya. Sekarang, bayangkan sebuah kurva yang melewati persegi panjang tersebut. Luas terarsir yang dibatasi oleh kurva, sumbu x, dan dua garis vertikal (yang membatasi persegi panjang) dapat dihitung menggunakan integral. Integral tersebut pada dasarnya adalah penjumlahan tak hingga dari luas-luas persegi panjang kecil yang sangat tipis yang membentuk area di bawah kurva.

Semakin kecil persegi panjang yang digunakan, semakin akurat perhitungan luasnya. Konsep ini adalah inti dari kalkulus integral.

Kesalahan Umum dan Solusi

Siswa seringkali membuat kesalahan dalam memahami konsep luas terarsir. Kesalahan-kesalahan ini dapat diatasi dengan pendekatan yang tepat.

• Kesalahan: Salah mengidentifikasi bentuk geometri yang terlibat.
• Solusi: Latih siswa untuk menggambar diagram dan mengidentifikasi bentuk-bentuk dasar yang menyusun area terarsir.
• Kesalahan: Menggunakan rumus yang salah atau tidak sesuai.
• Solusi: Tekankan pentingnya memahami konsep dasar rumus dan kapan harus menggunakannya. Berikan latihan soal yang bervariasi.
• Kesalahan: Lupa mengurangkan atau menambahkan luas yang tepat.
• Solusi: Minta siswa untuk selalu memeriksa kembali langkah-langkah mereka dan memastikan bahwa mereka telah mempertimbangkan semua area yang relevan. Gunakan visualisasi untuk membantu mereka memahami proses pengurangan dan penambahan.
• Kesalahan: Tidak memahami konsep proporsi dan rasio dalam soal yang melibatkan skala atau perbandingan.
• Solusi: Berikan latihan soal yang melibatkan proporsi dan rasio, serta menekankan pentingnya memahami hubungan antara ukuran dan skala.

Mengoptimalkan Pembelajaran Luas Terarsir

Memahami konsep luas terarsir adalah keterampilan penting dalam matematika, khususnya geometri. Menguasai materi ini tidak hanya tentang menghafal rumus, tetapi juga tentang mengembangkan kemampuan berpikir kritis dan memecahkan masalah. Untuk mencapai pemahaman yang mendalam, diperlukan pendekatan belajar yang efektif dan konsisten. Artikel ini akan memandu Anda melalui strategi belajar yang terbukti efektif, sumber belajar yang bermanfaat, dan contoh soal latihan untuk meningkatkan kemampuan Anda dalam menghitung luas terarsir.

Strategi Belajar Efektif

Menguasai luas terarsir membutuhkan lebih dari sekadar membaca materi. Dibutuhkan strategi belajar yang terencana dan konsisten. Berikut adalah beberapa tips untuk membantu Anda mencapai tujuan belajar:

• Atur Waktu Belajar yang Efektif: Buatlah jadwal belajar yang realistis dan konsisten. Alokasikan waktu khusus untuk belajar matematika, termasuk materi luas terarsir. Usahakan untuk belajar di waktu ketika Anda merasa paling fokus dan produktif. Hindari belajar terlalu lama tanpa istirahat. Gunakan teknik Pomodoro, yaitu belajar selama 25 menit diikuti istirahat 5 menit, untuk menjaga fokus.

• Pecahkan Soal Latihan Secara Teratur: Latihan adalah kunci untuk menguasai konsep luas terarsir. Mulailah dengan soal-soal dasar, kemudian tingkatkan ke soal yang lebih kompleks. Jangan ragu untuk mencoba berbagai jenis soal, termasuk soal yang melibatkan kombinasi bentuk geometri.
• Cari Bantuan Ketika Diperlukan: Jika Anda mengalami kesulitan, jangan ragu untuk mencari bantuan. Tanyakan kepada guru, teman, atau bergabunglah dengan kelompok belajar. Gunakan sumber-sumber online seperti forum diskusi atau video tutorial untuk mendapatkan penjelasan tambahan.
• Buat Catatan yang Rapi: Buatlah catatan yang jelas dan terstruktur. Gunakan diagram dan contoh soal untuk membantu Anda memahami konsep. Rangkum informasi penting dalam bentuk ringkasan atau peta konsep.
• Evaluasi dan Revisi: Lakukan evaluasi secara berkala untuk mengukur pemahaman Anda. Identifikasi area yang masih lemah dan fokuslah untuk memperbaikinya. Ulangi soal-soal yang sulit dan tinjau kembali catatan Anda.

Memanfaatkan Sumber Belajar

Tersedia banyak sumber belajar yang dapat membantu Anda memahami luas terarsir. Memanfaatkan sumber-sumber ini secara efektif dapat mempercepat proses belajar Anda. Berikut adalah beberapa sumber belajar yang direkomendasikan:

• Buku Teks: Buku teks adalah sumber informasi utama. Bacalah materi dengan seksama, perhatikan contoh soal, dan kerjakan soal latihan yang ada.
• Video Tutorial: Video tutorial, seperti yang tersedia di YouTube atau platform pendidikan lainnya, dapat memberikan penjelasan visual yang membantu Anda memahami konsep. Cari video yang menjelaskan konsep luas terarsir secara detail, termasuk contoh soal dan pembahasan.
• Situs Web dan Aplikasi: Banyak situs web dan aplikasi menyediakan materi belajar, contoh soal, dan kuis tentang luas terarsir. Manfaatkan sumber-sumber ini untuk latihan tambahan dan evaluasi diri.
• Forum Diskusi: Bergabunglah dengan forum diskusi online untuk berinteraksi dengan siswa lain dan guru. Ajukan pertanyaan, diskusikan soal-soal yang sulit, dan dapatkan umpan balik dari orang lain.
• Guru atau Tutor: Jika Anda membutuhkan bantuan tambahan, pertimbangkan untuk mencari guru atau tutor. Mereka dapat memberikan penjelasan yang lebih personal dan membantu Anda mengatasi kesulitan belajar.

Contoh Soal Latihan

Berikut adalah beberapa contoh soal latihan tentang luas terarsir, beserta kunci jawaban dan penjelasan singkatnya. Soal-soal ini bervariasi tingkat kesulitannya untuk membantu Anda menguji dan meningkatkan pemahaman Anda.

1. Soal 1 (Mudah): Sebuah persegi panjang memiliki panjang 10 cm dan lebar 6 cm. Di dalam persegi panjang tersebut terdapat sebuah lingkaran dengan diameter 4 cm. Hitunglah luas daerah yang diarsir (daerah di luar lingkaran tetapi di dalam persegi panjang).
   • Kunci Jawaban: 52.56 cm²
   • Penjelasan: Luas persegi panjang = panjang x lebar = 10 cm x 6 cm = 60 cm². Jari-jari lingkaran = diameter / 2 = 4 cm / 2 = 2 cm. Luas lingkaran = π x r² = 3.14 x 2² = 12.56 cm². Luas terarsir = Luas persegi panjang – Luas lingkaran = 60 cm²
     -12.56 cm² = 47.44 cm².

2. Soal 2 (Sedang): Sebuah segitiga siku-siku memiliki alas 8 cm dan tinggi 6 cm. Di dalam segitiga tersebut terdapat sebuah lingkaran yang menyinggung ketiga sisi segitiga. Hitunglah luas daerah yang diarsir (daerah di luar lingkaran tetapi di dalam segitiga).
   • Kunci Jawaban: 12.55 cm²
   • Penjelasan: Luas segitiga = 1/2 x alas x tinggi = 1/2 x 8 cm x 6 cm = 24 cm². Jari-jari lingkaran dalam segitiga siku-siku dapat dihitung dengan rumus r = (a + b – c) / 2, di mana a dan b adalah sisi siku-siku, dan c adalah sisi miring. Sisi miring = √(8² + 6²) = 10 cm.

     r = (8 + 6 – 10) / 2 = 2 cm. Luas lingkaran = π x r² = 3.14 x 2² = 12.56 cm². Luas terarsir = Luas segitiga – Luas lingkaran = 24 cm²
     -12.56 cm² = 11.44 cm².

3. Soal 3 (Sulit): Sebuah persegi memiliki sisi 10 cm. Di dalam persegi tersebut terdapat empat buah seperempat lingkaran yang berpusat di keempat titik sudut persegi. Hitunglah luas daerah yang diarsir (daerah di dalam persegi tetapi di luar keempat seperempat lingkaran).
   • Kunci Jawaban: 21.5 cm²
   • Penjelasan: Luas persegi = sisi² = 10² = 100 cm². Empat seperempat lingkaran membentuk satu lingkaran penuh dengan jari-jari 5 cm (setengah dari sisi persegi). Luas lingkaran = π x r² = 3.14 x 5² = 78.5 cm². Luas terarsir = Luas persegi – Luas lingkaran = 100 cm²
     -78.5 cm² = 21.5 cm².

Menjaga Motivasi Belajar

Belajar matematika, terutama materi yang dianggap sulit seperti luas terarsir, membutuhkan motivasi dan semangat yang tinggi. Berikut adalah beberapa tips untuk menjaga motivasi belajar:

Tetapkan Tujuan yang Jelas: Tentukan tujuan belajar yang spesifik dan terukur. Misalnya, “Saya akan menyelesaikan 10 soal latihan setiap hari” atau “Saya akan menguasai konsep luas terarsir dalam waktu satu minggu.”

Berikan Penghargaan pada Diri Sendiri: Berikan penghargaan pada diri sendiri setelah mencapai tujuan belajar. Penghargaan bisa berupa hal-hal kecil, seperti menonton film favorit atau makan makanan kesukaan.

Belajar Bersama Teman: Belajar bersama teman dapat meningkatkan motivasi dan semangat belajar. Diskusikan materi, saling membantu, dan saling memberikan dukungan.

Cari Inspirasi: Temukan inspirasi dari tokoh-tokoh yang sukses dalam bidang matematika atau ilmu pengetahuan. Baca kisah sukses mereka atau tonton video motivasi.

Jangan Takut Gagal: Kegagalan adalah bagian dari proses belajar. Jangan menyerah jika Anda mengalami kesulitan. Belajarlah dari kesalahan Anda dan teruslah mencoba.

Mengembangkan Kemampuan Berpikir Kritis

Perhitungan luas terarsir bukan hanya tentang menerapkan rumus; ini adalah arena untuk mengasah kemampuan berpikir kritis. Kemampuan ini memungkinkan siswa untuk memecahkan masalah kompleks, mengidentifikasi pola, dan mengembangkan solusi yang efektif. Dalam artikel ini, kita akan menjelajahi bagaimana cara menumbuhkan keterampilan berpikir kritis melalui soal-soal luas terarsir, dengan fokus pada analisis, identifikasi informasi penting, dan strategi pemecahan masalah.

Menganalisis Soal Luas Terarsir yang Menantang

Soal-soal yang menantang mendorong siswa untuk melampaui aplikasi rumus langsung. Mereka memerlukan pemahaman konsep yang mendalam dan kemampuan untuk memecah masalah menjadi bagian-bagian yang lebih kecil.Berikut adalah contoh soal:Sebuah persegi panjang ABCD memiliki panjang 16 cm dan lebar 12 cm. Di dalam persegi panjang tersebut terdapat dua buah lingkaran identik yang bersinggungan, masing-masing menyinggung dua sisi persegi panjang. Tentukan luas daerah yang diarsir, yaitu daerah di dalam persegi panjang tetapi di luar kedua lingkaran tersebut.Pembahasan:

1. Visualisasi

Gambarlah persegi panjang dan dua lingkaran di dalamnya. Pastikan lingkaran bersinggungan dan menyinggung sisi-sisi persegi panjang.

Memahami cara menghitung luas yang diarsir itu krusial, sama seperti pentingnya mengetahui detail lainnya. Bayangkan kamu perlu menghitung efisiensi bahan bakar mesinmu. Untuk itu, kamu perlu tahu bagaimana cara menghitung pemakaian bahan bakar per jam , kan? Nah, sama halnya dengan perhitungan luas, baik itu yang diarsir atau tidak, semuanya memerlukan ketelitian dan pemahaman konsep dasar. Jadi, jangan remehkan pentingnya menguasai kedua hal tersebut.

2. Identifikasi Informasi

Kita tahu panjang dan lebar persegi panjang, serta fakta bahwa kedua lingkaran identik.

3. Hitung Jari-jari Lingkaran

Karena dua lingkaran identik menyinggung sisi panjang persegi panjang, diameter setiap lingkaran adalah setengah dari panjang persegi panjang (16 cm / 2 = 8 cm). Jadi, jari-jari lingkaran adalah 4 cm.

4. Hitung Luas Persegi Panjang

Luas persegi panjang = panjang x lebar = 16 cm x 12 cm = 192 cm².

5. Hitung Luas Dua Lingkaran

Luas satu lingkaran = πr² = π(4 cm)² = 16π cm². Luas dua lingkaran = 2 x 16π cm² = 32π cm².

6. Hitung Luas Daerah Terarsir

Luas daerah terarsir = Luas persegi panjang – Luas dua lingkaran = 192 cm²32π cm². (Gunakan nilai π ≈ 3.14 untuk mendapatkan jawaban numerik).Soal ini memerlukan siswa untuk menggabungkan pengetahuan tentang persegi panjang dan lingkaran, serta kemampuan untuk memvisualisasikan masalah dan menerapkan strategi pemecahan masalah yang tepat.

Mengidentifikasi Informasi Penting dan Mengabaikan Informasi yang Tidak Relevan

Kemampuan untuk memilah informasi sangat penting dalam memecahkan soal matematika. Siswa harus mampu membedakan antara data yang relevan dan yang tidak.Berikut adalah beberapa tips:

• Baca Soal dengan Cermat: Pahami apa yang ditanyakan dan informasi apa yang diberikan.
• Garisbawahi Informasi Kunci: Tandai data yang penting untuk menyelesaikan soal.
• Visualisasikan: Buatlah gambar atau diagram untuk membantu memahami soal.
• Identifikasi Informasi yang Tidak Perlu: Abaikan data yang tidak relevan dengan perhitungan luas terarsir.

Contoh:Dalam soal yang menyebutkan harga pensil, tetapi tidak relevan dengan perhitungan luas, maka informasi harga pensil bisa diabaikan.

Tips untuk Mengembangkan Kemampuan Berpikir Kritis dalam Matematika

Mengembangkan kemampuan berpikir kritis memerlukan latihan dan pendekatan yang konsisten. Berikut adalah beberapa tips yang dapat membantu siswa:

1. Latihan Soal Secara Teratur: Semakin sering berlatih, semakin baik kemampuan memecahkan masalah.
2. Berpikir Kritis: Jangan hanya menghafal rumus, tetapi pahami konsep di baliknya.
3. Mencari Solusi Alternatif: Coba selesaikan soal dengan berbagai cara.
4. Menganalisis Kesalahan: Pelajari dari kesalahan untuk meningkatkan pemahaman.
5. Berdiskusi: Diskusikan soal dengan teman atau guru untuk mendapatkan perspektif yang berbeda.
6. Gunakan Teknologi: Manfaatkan kalkulator dan perangkat lunak geometri untuk membantu visualisasi dan perhitungan.

Ilustrasi Proses Berpikir Kritis dalam Memecahkan Soal Luas Terarsir

Proses berpikir kritis dalam memecahkan soal luas terarsir dapat diilustrasikan sebagai berikut:

1. Memahami Soal

Siswa membaca soal dengan cermat, mengidentifikasi apa yang diketahui dan apa yang ditanyakan.

2. Merencanakan Strategi

Siswa memilih pendekatan yang tepat, seperti membagi bentuk kompleks menjadi bentuk yang lebih sederhana.

3. Menerapkan Strategi

Siswa menggunakan rumus yang sesuai dan melakukan perhitungan.

4. Memeriksa Jawaban

Memahami cara menghitung luas yang diarsir memang membutuhkan fokus pada geometri dan logika. Namun, kemampuan ini lebih dari sekadar rumus; ini adalah fondasi berpikir analitis yang krusial. Sama seperti pentingnya Pendidikan dalam membangun fondasi pengetahuan, begitu pula pemahaman konsep matematika dasar. Dengan menguasai konsep ini, kita dapat memecahkan masalah kompleks, mulai dari soal ujian hingga aplikasi dunia nyata.

Jadi, jangan remehkan pentingnya menguasai cara menghitung luas yang diarsir!

Siswa memeriksa kembali jawaban untuk memastikan keakuratan dan kelogisan.

5. Merefleksikan

Siswa mempertimbangkan cara-cara alternatif untuk menyelesaikan soal dan menarik kesimpulan.Misalnya, pada soal yang melibatkan kombinasi persegi dan lingkaran, siswa akan:* Memahami: Memahami bahwa soal meminta luas daerah yang tersisa setelah lingkaran dipotong dari persegi.

Merencanakan

Merencanakan untuk menghitung luas persegi terlebih dahulu, kemudian menghitung luas lingkaran, dan akhirnya mengurangkan luas lingkaran dari luas persegi.

Menerapkan

Menggunakan rumus luas persegi (sisi x sisi) dan rumus luas lingkaran (πr²).

Memeriksa

Memastikan bahwa jawaban masuk akal (misalnya, luas daerah terarsir harus lebih kecil dari luas persegi).

Merefleksikan

Memikirkan apakah ada cara lain untuk memecahkan soal, misalnya, dengan menggunakan pendekatan yang berbeda dalam menghitung luas lingkaran.

Menjelajahi Lebih Dalam: Konsep Lanjutan dalam Luas Terarsir: Cara Menghitung Luas Yg Diarsir

Setelah menguasai dasar-dasar perhitungan luas terarsir, saatnya untuk menyelami konsep-konsep yang lebih kompleks dan aplikasinya dalam berbagai bidang. Pemahaman mendalam tentang konsep lanjutan ini akan membuka wawasan baru, memungkinkan Anda memecahkan masalah yang lebih rumit, dan memperkaya kemampuan berpikir analitis Anda. Mari kita mulai perjalanan eksplorasi ini!

Memahami cara menghitung luas yang diarsir memang membutuhkan fokus dan ketelitian. Sama halnya dengan menyusun RPP yang efektif. RPP yang baik akan memandu guru dalam menjelaskan konsep matematika secara terstruktur, termasuk bagaimana cara mengurai soal luas arsiran. Dengan begitu, siswa bisa lebih mudah memahami dan mengaplikasikan konsep luas arsiran dalam berbagai situasi.

Konsep-konsep lanjutan dalam perhitungan luas terarsir membuka pintu menuju pemahaman yang lebih dalam tentang dunia matematika dan aplikasinya dalam kehidupan nyata. Dari menghitung volume benda tiga dimensi hingga memahami konsep integral, kemampuan untuk menguasai materi ini akan sangat berharga.

Konsep Lanjutan: Luas Permukaan, Volume, dan Integral

Konsep-konsep lanjutan ini memungkinkan kita untuk tidak hanya menghitung luas daerah dua dimensi, tetapi juga menganalisis bentuk tiga dimensi dan bahkan memahami perubahan luas secara kontinu. Berikut adalah beberapa konsep kunci:

• Luas Permukaan: Melibatkan perhitungan total luas dari seluruh permukaan luar suatu objek tiga dimensi. Konsep ini sangat penting dalam berbagai aplikasi, seperti perhitungan bahan yang dibutuhkan untuk membuat kemasan atau menganalisis transfer panas pada suatu benda.
• Volume: Mengukur ruang yang ditempati oleh suatu objek tiga dimensi. Pemahaman tentang volume sangat penting dalam bidang teknik, arsitektur, dan sains, misalnya untuk menghitung kapasitas wadah atau volume bahan bangunan.
• Integral: Konsep matematika yang digunakan untuk menghitung luas di bawah kurva, volume benda putar, dan banyak lagi. Integral adalah alat yang sangat ampuh dalam kalkulus dan memiliki aplikasi luas dalam fisika, teknik, dan ekonomi.

Penerapan konsep-konsep ini sangat luas. Misalnya, dalam arsitektur, perhitungan luas permukaan dan volume sangat penting untuk merancang bangunan yang efisien dan estetis. Dalam teknik, konsep integral digunakan untuk menganalisis struktur dan memprediksi perilaku material. Di bidang sains, konsep-konsep ini digunakan untuk memodelkan fenomena alam dan melakukan eksperimen.

Contoh Soal dan Penyelesaian: Mengaplikasikan Konsep Lanjutan

Mari kita lihat beberapa contoh soal yang melibatkan penggunaan konsep-konsep lanjutan, beserta penyelesaiannya secara rinci:

1. Soal: Sebuah tangki air berbentuk tabung memiliki diameter 2 meter dan tinggi 3 meter. Berapa luas permukaan dan volume tangki tersebut?
2. Penyelesaian:
   • Luas Permukaan: Luas permukaan tabung terdiri dari dua lingkaran (atas dan bawah) dan selimut tabung.
   • Luas lingkaran = πr², dengan r adalah jari-jari (setengah dari diameter). Jadi, r = 1 meter. Luas dua lingkaran = 2π(1)² = 2π meter persegi.
   • Luas selimut tabung = 2πrh, dengan h adalah tinggi tabung. Jadi, luas selimut = 2π(1)(3) = 6π meter persegi.
   • Luas permukaan total = 2π + 6π = 8π meter persegi, atau sekitar 25.13 meter persegi.
   • Volume: Volume tabung = πr²h = π(1²)(3) = 3π meter kubik, atau sekitar 9.42 meter kubik.
3. Soal: Hitung volume benda putar yang dihasilkan dengan memutar kurva y = x² dari x = 0 hingga x = 2 mengelilingi sumbu x.
4. Penyelesaian:
   • Gunakan metode cakram (disk method). Volume setiap cakram kecil adalah πy²dx = π(x²)²dx = πx⁴dx.
   • Integrasikan dari x = 0 hingga x = 2: ∫₀² πx⁴ dx = π[x⁵/5]₀² = π(32/5 – 0) = (32/5)π, atau sekitar 20.11 satuan volume.

Contoh-contoh ini menunjukkan bagaimana konsep-konsep lanjutan dapat digunakan untuk memecahkan masalah praktis. Dengan berlatih lebih banyak soal, Anda akan semakin mahir dalam mengaplikasikan konsep-konsep ini.

Sumber Belajar Tambahan

Untuk memperdalam pemahaman Anda tentang konsep-konsep lanjutan dalam perhitungan luas terarsir, berikut adalah beberapa sumber belajar yang direkomendasikan:

• Buku Teks Kalkulus: Buku teks kalkulus tingkat lanjut menyediakan penjelasan rinci tentang integral, turunan, dan aplikasi mereka.
• Khan Academy: Platform pembelajaran online gratis yang menawarkan video dan latihan tentang kalkulus dan konsep matematika lainnya.
• MIT OpenCourseware: Akses ke materi kuliah, catatan, dan tugas dari kursus matematika di MIT.
• Jurnal Ilmiah: Jurnal seperti “Journal of Mathematical Analysis and Applications” dapat memberikan wawasan tentang penelitian terbaru dalam bidang matematika.

Manfaatkan sumber-sumber ini untuk memperluas pengetahuan Anda dan mengembangkan keterampilan memecahkan masalah.

Perbandingan Konsep Dasar dan Lanjutan

Tabel berikut membandingkan konsep dasar dan lanjutan dalam perhitungan luas terarsir:

Konsep Dasar	Konsep Lanjutan	Aplikasi
Luas bangun datar sederhana (persegi, persegi panjang, segitiga)	Luas permukaan, volume, integral	Desain arsitektur, rekayasa teknik, fisika, ekonomi
Rumus luas dasar (panjang x lebar, 1/2 x alas x tinggi)	Metode cakram, metode kulit tabung, integral lipat	Perhitungan volume kompleks, analisis struktur, pemodelan fenomena alam
Pengukuran langsung dan manipulasi bentuk sederhana	Penggunaan kalkulus untuk menghitung luas dan volume yang kompleks	Pemecahan masalah yang melibatkan bentuk tidak beraturan dan perubahan kontinu

Tabel ini memberikan gambaran jelas tentang perbedaan utama antara konsep dasar dan lanjutan, serta bagaimana konsep lanjutan membuka kemungkinan baru dalam perhitungan luas terarsir.

Memahami cara menghitung luas yang diarsir memang membutuhkan ketelitian, namun jauh lebih sederhana dibandingkan dengan kompleksitas dunia siber. Bayangkan, daripada fokus pada rumus-rumus geometri, ada pihak-pihak yang justru memanfaatkan teknologi untuk tujuan yang kurang baik. Sebagai contoh, ada artikel menarik tentang cara ddos dengan android , yang menunjukkan bagaimana perangkat sederhana bisa disalahgunakan. Kembali ke soal matematika, menghitung luas yang diarsir tetaplah penting untuk menguasai konsep dasar.

Membangun Portofolio Soal

Membuat portofolio soal adalah langkah krusial dalam menguasai perhitungan luas terarsir. Ini bukan hanya tentang menyelesaikan soal, tetapi juga tentang memahami pola, strategi, dan variasi soal yang ada. Dengan memiliki portofolio soal yang terstruktur, Anda dapat melacak kemajuan, mengidentifikasi kelemahan, dan terus meningkatkan kemampuan menyelesaikan soal-soal perhitungan luas terarsir.

Dalam bagian ini, kita akan membahas cara merancang, menyusun, dan mengelola portofolio soal perhitungan luas terarsir yang efektif.

Merancang Template Soal Latihan

Template soal yang baik adalah fondasi dari portofolio soal yang efektif. Template ini akan membantu Anda membuat soal latihan secara konsisten dan terstruktur. Berikut adalah elemen-elemen kunci yang perlu ada dalam template soal latihan:

• Format Soal: Sertakan ruang untuk soal itu sendiri, baik dalam bentuk gambar (sketsa bentuk geometris yang diarsir) maupun deskripsi teks. Pastikan soal jelas dan mudah dipahami. Contoh: “Hitung luas daerah yang diarsir pada persegi panjang dengan panjang 10 cm dan lebar 5 cm, dengan setengah lingkaran di salah satu sisinya.”
• Ruang untuk Jawaban: Sediakan ruang yang cukup untuk menuliskan langkah-langkah penyelesaian dan jawaban akhir. Ini membantu dalam melacak proses berpikir dan mengidentifikasi kesalahan.
• Kolom untuk Catatan: Sertakan kolom untuk mencatat konsep yang digunakan, kesulitan soal (misalnya, mudah, sedang, sulit), dan catatan pribadi (misalnya, strategi yang berhasil atau kesalahan yang sering terjadi).
• Nomor Soal dan Tanggal: Berikan nomor unik pada setiap soal dan catat tanggal penyelesaian. Ini membantu dalam melacak kemajuan dan revisi.

Dengan template ini, Anda dapat secara efisien membuat dan mengelola kumpulan soal latihan.

Contoh Soal Referensi

Memiliki daftar contoh soal adalah kunci untuk membangun portofolio yang komprehensif. Daftar ini berfungsi sebagai sumber inspirasi dan referensi untuk membuat soal-soal latihan baru. Berikut adalah beberapa contoh soal yang bisa Anda gunakan sebagai referensi:

1. Soal Dasar: Hitung luas daerah yang diarsir pada persegi dengan sisi 8 cm. (Mudah)
2. Soal Tingkat Menengah: Hitung luas daerah yang diarsir pada gabungan persegi panjang dan segitiga siku-siku. (Sedang)
3. Soal Tingkat Lanjut: Hitung luas daerah yang diarsir pada lingkaran dengan beberapa sektor yang diarsir. (Sulit)
4. Soal Kombinasi: Hitung luas daerah yang diarsir pada bentuk yang terdiri dari gabungan persegi, lingkaran, dan segitiga. (Sedang/Sulit)
5. Soal Aplikasi: Sebuah taman berbentuk lingkaran dengan diameter 14 meter. Di tengah taman terdapat kolam berbentuk persegi dengan sisi 4 meter. Hitung luas area taman yang tidak tertutup kolam. (Sedang)

Pastikan untuk mencatat sumber soal (jika ada) dan tingkat kesulitan pada setiap soal.

Tips Menyusun Soal yang Efektif

Menyusun soal yang efektif memerlukan perencanaan dan perhatian terhadap detail. Berikut adalah beberapa tips untuk menyusun soal yang efektif:

Tips 1: Mulailah dengan soal-soal dasar untuk membangun fondasi yang kuat. Tingkatkan tingkat kesulitan secara bertahap.

Tips 2: Gunakan variasi bentuk geometris (persegi, persegi panjang, lingkaran, segitiga, trapesium, dll.) untuk menguji pemahaman konsep secara menyeluruh.

Tips 3: Sertakan soal yang membutuhkan lebih dari satu langkah penyelesaian untuk menguji kemampuan berpikir kritis.

Tips 4: Pastikan soal jelas, ringkas, dan mudah dipahami. Hindari penggunaan bahasa yang ambigu.

Tips 5: Gunakan soal-soal aplikasi yang relevan dengan kehidupan sehari-hari untuk membuat pembelajaran lebih menarik.

Dengan mengikuti tips ini, Anda dapat menyusun soal yang efektif dan sesuai dengan tingkat kesulitan yang diinginkan.

Menyusun dan Mengakses Portofolio Soal

Penyusunan dan aksesibilitas adalah kunci dari portofolio soal yang efektif. Berikut adalah cara menyusun portofolio soal yang terstruktur dan mudah diakses:

• Pilih Metode Penyimpanan: Anda dapat menyimpan soal dalam format digital (misalnya, dokumen Word, spreadsheet, atau aplikasi catatan) atau dalam bentuk fisik (misalnya, buku catatan atau map). Pilihlah metode yang paling sesuai dengan preferensi Anda.
• Gunakan Sistem Pengelompokan: Kelompokkan soal berdasarkan topik (misalnya, persegi, lingkaran, gabungan bentuk), tingkat kesulitan (mudah, sedang, sulit), atau konsep yang digunakan (misalnya, luas, keliling, teorema Pythagoras).
• Berikan Label dan Indeks: Beri label pada setiap soal dengan nomor unik dan catat tanggal penyelesaian. Buat indeks atau daftar isi untuk memudahkan pencarian soal.
• Perbarui Secara Teratur: Tambahkan soal baru secara teratur dan tinjau kembali soal-soal yang sudah ada. Catat kemajuan dan identifikasi area yang perlu ditingkatkan.
• Manfaatkan Teknologi: Jika menggunakan format digital, manfaatkan fitur pencarian untuk menemukan soal dengan cepat. Gunakan aplikasi catatan untuk membuat catatan dan menambahkan komentar pada setiap soal.

Dengan mengikuti langkah-langkah ini, Anda dapat membangun portofolio soal yang terstruktur, mudah diakses, dan efektif untuk meningkatkan kemampuan perhitungan luas terarsir.

Kesimpulan

Setelah menjelajahi berbagai sudut pandang, dari dasar hingga konsep lanjutan, Anda kini memiliki bekal yang kuat untuk menaklukkan soal-soal “cara menghitung luas yang diarsir”. Ingatlah, kunci keberhasilan bukanlah menghafal rumus, melainkan memahami konsep dan mampu berpikir kritis. Teruslah berlatih, jangan takut membuat kesalahan, dan nikmati proses belajar. Dunia matematika luas terbentang di hadapan Anda, siap untuk dijelajahi dan ditaklukkan. Selamat! Anda sekarang memiliki senjata rahasia untuk menaklukkan setiap tantangan geometri yang datang.

FAQ dan Informasi Bermanfaat

Apa perbedaan antara luas dan keliling?

Luas mengukur area di dalam sebuah bentuk, sedangkan keliling mengukur panjang sisi-sisi luar bentuk tersebut.

Mengapa penting untuk memahami konsep dasar sebelum menghafal rumus?

Pemahaman konsep membantu Anda mengingat rumus dengan lebih mudah dan mampu memecahkan soal-soal yang lebih kompleks, bukan hanya soal yang sesuai dengan rumus.

Bagaimana cara mengidentifikasi bangun datar yang tersembunyi dalam bentuk yang lebih kompleks?

Perhatikan dengan cermat bentuk-bentuk dasar seperti segitiga, persegi, lingkaran, dan gabungan bentuk lainnya. Bagi bentuk kompleks menjadi bagian-bagian yang lebih sederhana.

Apa saja kesalahan umum yang sering terjadi saat menghitung luas terarsir?

Kesalahan umum termasuk salah mengidentifikasi bentuk, menggunakan rumus yang salah, atau salah dalam melakukan perhitungan. Perhatikan tanda baca dan satuan.

Bagaimana cara meningkatkan kemampuan berpikir kritis dalam soal luas terarsir?

Latih diri untuk menganalisis soal dengan cermat, mengidentifikasi informasi penting, dan merencanakan langkah-langkah penyelesaian. Jangan ragu untuk mencoba berbagai pendekatan.