Silabus Matematika Kelas 7 Semester 2 Kurikulum 2013

Silabus matematika kelas 7 semester 2 kurikulum 2013 merupakan panduan penting bagi guru dan siswa dalam memahami materi yang akan dipelajari. Materi-materi ini akan membentuk dasar pemahaman matematika yang lebih lanjut. Bagaimana materi ini disusun untuk mempersiapkan siswa menghadapi tantangan matematika di masa depan? Mari kita telusuri lebih dalam.

Silabus ini mencakup beragam topik penting dalam matematika, mulai dari operasi bilangan bulat hingga persamaan dan pertidaksamaan linear satu variabel. Pemahaman terhadap materi prasyarat dari semester 1 sangatlah krusial untuk menguasai materi semester 2. Mari kita lihat lebih detail tentang struktur dan isi silabus ini, sehingga kita dapat memahami dengan lebih baik tujuan pembelajaran dan keterkaitannya dengan kehidupan sehari-hari.

Table of Contents

Untuk Memperkaya dan Mengembangkan Pemahaman Matematika Kelas 7 Semester 2

Silabus Matematika Kelas 7 Semester 2 Kurikulum 2013 dirancang untuk memperkuat pemahaman siswa terhadap konsep-konsep matematika dasar yang akan digunakan dalam pembelajaran selanjutnya. Materi yang disajikan dibagi menjadi beberapa topik utama, dilengkapi dengan alokasi waktu dan bobot nilai untuk setiap topik. Hal ini bertujuan untuk membantu siswa dalam menguasai materi dengan efektif dan terarah.

Gambaran Umum Materi

Silabus ini mencakup berbagai topik penting dalam matematika, mulai dari operasi bilangan hingga geometri. Materi disusun secara sistematis dan bertahap, sehingga siswa dapat membangun pemahaman yang kokoh dan terintegrasi. Tujuan utama adalah untuk mempersiapkan siswa menghadapi materi matematika yang lebih kompleks di jenjang berikutnya.

Topik-Topik Utama

Operasi Bilangan Bulat dan Pecahan
Persamaan dan Pertidaksamaan Linear Satu Variabel
Himpunan dan Operasinya
Geometri Bidang Datar
Statistika dan Peluang Dasar

Tabel Urutan dan Bobot Materi

No.	Topik Materi	Durasi (Jam)	Bobot (%)	Tujuan Pembelajaran
1	Operasi Bilangan Bulat dan Pecahan	15	15%	Siswa mampu melakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan bulat dan pecahan dengan benar, serta memahami konsepnya. Contohnya dalam menghitung keuntungan atau kerugian dalam transaksi jual beli.
2	Persamaan dan Pertidaksamaan Linear Satu Variabel	20	20%	Siswa mampu menyelesaikan persamaan dan pertidaksamaan linear satu variabel dengan metode yang tepat dan memahami penerapannya dalam soal cerita. Contohnya dalam menghitung jarak tempuh atau mencari harga suatu barang.
3	Himpunan dan Operasinya	10	10%	Siswa mampu mengidentifikasi, mendeskripsikan, dan melakukan operasi pada himpunan, serta memahami konsep-konsep yang terkait. Contohnya dalam menentukan anggota suatu kelompok atau dalam memilih produk yang memenuhi syarat tertentu.
4	Geometri Bidang Datar	18	25%	Siswa mampu mengidentifikasi dan mengklasifikasikan bangun datar, menghitung keliling dan luasnya, serta memahami hubungan antar bangun datar. Contohnya dalam mendesain sebuah ruangan atau menghitung luas tanah untuk membangun rumah.
5	Statistika dan Peluang Dasar	12	10%	Siswa mampu mengumpulkan, menyajikan, dan menganalisis data dalam bentuk tabel dan diagram, serta memahami konsep peluang sederhana. Contohnya dalam menganalisis hasil survei atau menentukan kemungkinan suatu kejadian terjadi.

Tujuan Pembelajaran Detail

Setiap topik di atas memiliki tujuan pembelajaran detail yang diuraikan lebih lanjut. Tujuan ini disusun agar siswa dapat menguasai materi secara menyeluruh dan terukur. Contohnya pada topik Persamaan dan Pertidaksamaan Linear Satu Variabel, siswa diharapkan mampu menyelesaikan berbagai tipe soal cerita yang melibatkan persamaan dan pertidaksamaan. Hal ini penting untuk mengembangkan kemampuan berpikir kritis dan pemecahan masalah siswa.

Materi Prasyarat

Pemahaman tentang operasi hitung bilangan bulat dan pecahan.
Penggunaan sifat-sifat operasi hitung.
Pemahaman tentang konsep variabel dan konstanta.
Penggunaan diagram Venn untuk mengilustrasikan hubungan antar himpunan.

Deskripsi Topik Materi Matematika Kelas 7 Semester 2

Semester dua matematika kelas tujuh menjanjikan perjalanan menarik ke dalam dunia geometri, aljabar, dan statistik. Materi-materi ini akan memperkuat pemahaman siswa tentang konsep-konsep dasar matematika yang akan menjadi pondasi untuk pembelajaran selanjutnya. Pemahaman yang mendalam terhadap topik-topik ini akan memungkinkan siswa untuk memecahkan masalah sehari-hari dengan lebih efektif.

Geometri: Bangun Datar dan Ruang

Topik ini akan menyelidiki berbagai bangun datar dan ruang. Siswa akan mempelajari sifat-sifat, rumus, dan hubungan antara bangun-bangun tersebut. Pemahaman tentang konsep-konsep ini sangat krusial untuk mengembangkan kemampuan spasial dan pemecahan masalah geometri.

Bangun Datar: Siswa akan mempelajari berbagai bangun datar seperti segitiga, persegi panjang, trapesium, dan lingkaran. Mereka akan mengidentifikasi sifat-sifat masing-masing bangun, termasuk sudut, sisi, dan diagonalnya. Rumus untuk menghitung keliling dan luas akan dipelajari. Contoh: Menghitung keliling dan luas persegi panjang dengan panjang 5 cm dan lebar 3 cm.
Bangun Ruang: Topik ini mencakup kubus, balok, prisma, limas, dan tabung. Siswa akan mempelajari sifat-sifat masing-masing bangun ruang, termasuk volume dan luas permukaannya. Contoh: Menentukan volume kubus dengan rusuk 4 cm.
Hubungan Antar Bangun: Siswa akan belajar tentang hubungan antara bangun datar dan ruang, seperti bagaimana bangun datar dapat membentuk bangun ruang. Contoh: Membuat jaring-jaring kubus dan balok.

Aljabar: Operasi Aljabar dan Persamaan Linear Satu Variabel

Topik ini akan memperkenalkan konsep dasar aljabar, khususnya operasi aljabar dan persamaan linear satu variabel. Kemampuan untuk memahami dan menyelesaikan persamaan akan sangat membantu dalam memecahkan masalah sehari-hari yang melibatkan hubungan antara variabel.

Operasi Aljabar: Siswa akan mempelajari penjumlahan, pengurangan, perkalian, dan pembagian aljabar. Ini melibatkan variabel dan konstanta. Contoh: Menyederhanakan ekspresi 3x + 2y – x + 5y.
Persamaan Linear Satu Variabel: Siswa akan belajar menyelesaikan persamaan linear satu variabel. Ini melibatkan penentuan nilai variabel yang membuat persamaan tersebut benar. Contoh: Menyelesaikan persamaan 2x + 5 = 11.
Penerapan Persamaan Linear: Siswa akan mempelajari bagaimana persamaan linear dapat digunakan untuk menyelesaikan masalah sehari-hari. Contoh: Menentukan usia seseorang jika diketahui 5 tahun yang lalu usianya 10 tahun lebih tua dari separuh usia adiknya.

Statistika: Penyajian Data

Topik ini akan memperkenalkan konsep dasar statistika, khususnya penyajian data. Kemampuan untuk menyajikan data dengan tepat dan efisien sangat penting untuk memahami informasi yang disajikan dalam bentuk data.

Silabus matematika kelas 7 semester 2 kurikulum 2013, mengajarkan berbagai konsep dasar. Namun, seiring pesatnya perkembangan ilmu pengetahuan dan teknologi (iptek), kita perlu memikirkan bagaimana agar kemajuan tersebut tidak melupakan nilai-nilai keagamaan. Bagaimana caranya agar pembelajaran matematika, dan ilmu pengetahuan pada umumnya, tetap selaras dengan nilai-nilai luhur? Perlukah kita merevisi silabus untuk mempertimbangkan hal ini?

Solusi seperti apa yang bisa diterapkan? Mari kita lihat bagaimana kita dapat memastikan bahwa kemajuan iptek tidak merusak nilai-nilai keagamaan agar kemajuan iptek tidak merusak nilai nilai keagamaan maka sebaiknya. Pembelajaran matematika yang berimbang dan berwawasan luas akan membantu membentuk generasi yang memahami pentingnya keseimbangan antara ilmu pengetahuan dan nilai-nilai spiritual. Hal ini tentunya akan sangat berpengaruh pada silabus matematika kelas 7 semester 2 kurikulum 2013.

Pengumpulan Data: Siswa akan mempelajari berbagai cara mengumpulkan data, seperti survei dan pengamatan.
Penyajian Data: Siswa akan mempelajari cara menyajikan data dalam bentuk tabel, diagram batang, diagram lingkaran, dan diagram garis. Contoh: Menyajikan data hasil survei tentang warna kesukaan siswa menggunakan diagram lingkaran.
Interpretasi Data: Siswa akan belajar untuk menginterpretasikan data yang disajikan dalam berbagai bentuk. Contoh: Menganalisis data dari diagram batang untuk menentukan tren.

Contoh Soal dan Pembahasan Matematika Kelas 7 Semester 2

Memahami konsep matematika tidak cukup hanya dengan menghafal rumus. Penting untuk bisa menerapkannya dalam berbagai situasi. Berikut ini beberapa contoh soal dan pembahasan yang akan membantu Anda memahami lebih dalam materi-materi penting dalam silabus matematika kelas 7 semester 2.

Silabus matematika kelas 7 semester 2 kurikulum 2013, memang penuh tantangan, kan? Kita perlu memahami konsep-konsep baru. Bayangkan, seperti dalam sebuah pertandingan sepak bola, kita perlu strategi yang tepat untuk “menahan” pemahaman materi. Nah, di lapangan sepak bola, pemain yang bertugas menahan bola disebut pemain yang bertugas menahan bola disebut , begitu juga dalam memahami silabus, kita perlu strategi yang tepat untuk menyerap materi dengan baik.

Akhirnya, kembali ke silabus matematika, kita perlu menguasai setiap materi untuk mencapai hasil yang maksimal.

Operasi Hitung Bilangan Bulat

Operasi hitung bilangan bulat, meliputi penjumlahan, pengurangan, perkalian, dan pembagian, merupakan dasar penting dalam matematika. Pemahaman yang kuat akan membantu dalam memecahkan masalah yang lebih kompleks.

Soal: Tentukan hasil dari -15 + 8 – (-12).
Pembahasan: Untuk menyelesaikan soal ini, kita harus memperhatikan aturan operasi hitung bilangan bulat. Pertama, kita hitung -15 + 8. Hasilnya adalah -7. Kemudian, kita hitung -7 – (-12).

Pengurangan dengan bilangan negatif sama dengan penjumlahan dengan lawannya. Jadi, -7 – (-12) sama dengan -7 + 12. Hasil akhirnya adalah

5.
Langkah-langkah penyelesaian
1. Hitung -15 + 8 = -7
2. Hitung -7 – (-12) = -7 + 12 = 5
Soal: Berapakah hasil dari -3 x 5 ?
Pembahasan: Perkalian bilangan bulat negatif dengan bilangan bulat positif menghasilkan bilangan bulat negatif. -3 x 5 = -15
Langkah-langkah penyelesaian:
1. Kalikan -3 dengan 5.

Pecahan

Pemahaman tentang pecahan sangat krusial untuk materi-materi selanjutnya. Kemampuan dalam mengoperasikan pecahan akan mempermudah dalam memecahkan berbagai permasalahan sehari-hari.

Soal: Sederhanakan pecahan 12/
18.
Pembahasan

Untuk menyederhanakan pecahan, kita harus mencari faktor persekutuan terbesar (FPB) dari pembilang dan penyebut. FPB dari 12 dan 18 adalah 6. Bagi pembilang dan penyebut dengan 6. 12/6 = 2 dan 18/6 = 3. Jadi, pecahan 12/18 dapat disederhanakan menjadi 2/

3.
Langkah-langkah penyelesaian
1. Cari FPB dari 12 dan 18, yaitu 6.
2. Bagi pembilang dan penyebut dengan 6.
3. Hasilnya adalah 2/3.

Penggunaan Koordinat Cartesius

Koordinat Cartesius digunakan untuk menentukan posisi suatu titik pada bidang datar. Memahami konsep ini penting untuk mempelajari materi geometri.

Soal: Tentukan koordinat titik yang berada di kuadran II.
Pembahasan: Kuadran II berada di sebelah kiri sumbu y dan di atas sumbu x. Titik di kuadran II memiliki absis (x) negatif dan ordinat (y) positif. Contoh: (-2, 3).

Persamaan Linier Satu Variabel

Persamaan linier satu variabel merupakan dasar dalam aljabar. Pemahamannya akan membantu dalam menyelesaikan berbagai masalah yang melibatkan persamaan.

Soal: Selesaikan persamaan 2x + 5 = 11.
Pembahasan: Untuk menyelesaikan persamaan ini, kita perlu mengisolasi variabel x. Kurangi 5 dari kedua ruas persamaan: 2x + 5 – 5 = 11 – 5, sehingga 2x =
6. Kemudian bagi kedua ruas dengan 2

2x/2 = 6/2, sehingga x = 3.

Ringkasan Rumus

Topik	Rumus
Penjumlahan Bilangan Bulat	a + b
Pengurangan Bilangan Bulat	a – b
Perkalian Bilangan Bulat	a x b
Pembagian Bilangan Bulat	a ÷ b
Menyederhanakan Pecahan	Membagi pembilang dan penyebut dengan FPB

Aktivitas Pembelajaran

Aktivitas pembelajaran yang menarik dan interaktif sangat penting untuk menumbuhkan pemahaman konsep matematika pada siswa kelas 7. Kegiatan-kegiatan ini tidak hanya berfokus pada pemahaman teoritis, tetapi juga mendorong siswa untuk berpikir kritis, memecahkan masalah, dan berkolaborasi.

Kegiatan Diskusi

Diskusi kelompok kecil dapat digunakan untuk mengasah pemahaman siswa terhadap konsep-konsep baru. Melalui diskusi, siswa dapat saling bertukar ide, menjelaskan pemahaman mereka, dan mengidentifikasi kelemahan dalam pemahaman masing-masing. Contohnya, dalam mempelajari sistem persamaan linear, siswa dapat dibagi menjadi beberapa kelompok untuk mendiskusikan berbagai metode penyelesaian, seperti metode substitusi dan eliminasi.

Siswa dibagi dalam kelompok-kelompok kecil.
Setiap kelompok diberi topik dan tugas untuk dibahas dan dipecahkan bersama.
Guru berperan sebagai fasilitator untuk memandu diskusi dan menjawab pertanyaan siswa.
Setiap kelompok diminta untuk menyimpulkan hasil diskusi dan mempresentasikannya di depan kelas.

Kegiatan Proyek

Proyek merupakan cara efektif untuk menerapkan konsep matematika dalam kehidupan nyata. Siswa dapat terlibat dalam proyek-proyek yang menantang dan mendorong mereka untuk berpikir kreatif dan memecahkan masalah kompleks. Contohnya, dalam mempelajari geometri, siswa dapat membuat model bangun ruang dan menghitung luas permukaan atau volumenya.

Siswa dibagi dalam kelompok-kelompok.
Guru memberikan tugas proyek yang relevan dengan topik yang sedang dipelajari.
Siswa bekerja sama dalam kelompok untuk menyelesaikan proyek tersebut.
Proyek dapat berupa pembuatan model, presentasi, atau pembuatan laporan.
Contoh proyek: Membuat model rumah dengan menghitung luas dan volume ruangan-ruangannya, merancang dan membangun jembatan dengan bahan-bahan tertentu untuk menahan beban tertentu.

Sumber Belajar

Sumber belajar yang relevan sangat penting untuk mendukung pemahaman siswa. Sumber-sumber ini dapat berupa buku teks, artikel jurnal, situs web, dan video edukatif. Buku teks yang terstruktur dengan baik dan disertai contoh soal yang beragam dapat memberikan pemahaman yang lebih mendalam.

Buku teks matematika kelas 7.
Buku referensi terkait topik yang sedang dipelajari.
Situs web pendidikan seperti Khan Academy, dan situs web lainnya yang relevan.
Video edukatif yang menjelaskan konsep matematika secara visual.

Media Pembelajaran

Penggunaan media pembelajaran dapat memperjelas konsep-konsep matematika yang abstrak. Media pembelajaran dapat berupa gambar, grafik, video, atau alat peraga. Contohnya, penggunaan alat peraga bangun ruang dapat membantu siswa memahami bentuk dan ukuran bangun tersebut.

Gambar dan grafik untuk menjelaskan konsep abstrak.
Alat peraga geometri, seperti bangun ruang dan garis bilangan.
Video animasi yang menjelaskan konsep matematika.
Aplikasi interaktif yang memungkinkan siswa berinteraksi langsung dengan konsep matematika.

Bagan Alir Proyek

Berikut contoh bagan alir untuk menyelesaikan proyek pembuatan model rumah:

Langkah	Deskripsi
1. Perencanaan	Menentukan desain rumah, bahan-bahan yang dibutuhkan, dan estimasi waktu.
2. Pengumpulan Data	Mengumpulkan data tentang ukuran dan bentuk ruangan, serta bahan bangunan yang akan digunakan.
3. Desain dan Perancangan	Membuat desain 2D dan 3D dari model rumah, termasuk perhitungan luas dan volume.
4. Pembuatan Model	Membuat model rumah sesuai dengan desain yang telah direncanakan.
5. Evaluasi dan Modifikasi	Mengevaluasi model rumah dan melakukan modifikasi jika diperlukan.
6. Presentasi	Mempresentasikan model rumah dan hasil perhitungan kepada kelas.

Evaluasi Pembelajaran Matematika

Evaluasi pembelajaran matematika bukan sekadar mengukur kemampuan siswa, tetapi juga menjadi alat untuk mengidentifikasi kekuatan dan kelemahan pemahaman mereka. Dengan evaluasi yang tepat, guru dapat memberikan umpan balik berharga dan menyesuaikan strategi pengajaran untuk mendukung perkembangan siswa secara optimal.

Jenis-jenis Evaluasi

Evaluasi dalam matematika dapat dilakukan dengan berbagai metode, memastikan cakupan pemahaman siswa dari berbagai aspek. Beberapa jenis evaluasi yang efektif antara lain tes tertulis dan praktik.

Tes Tertulis: Metode ini memungkinkan pengukuran pemahaman konseptual dan kemampuan pemecahan masalah siswa secara terstruktur. Berbagai bentuk soal, seperti pilihan ganda, isian singkat, essay, dan soal uraian, dapat digunakan untuk menguji pemahaman siswa terhadap berbagai materi.
Evaluasi Praktik: Metode ini mengukur kemampuan siswa dalam menerapkan konsep matematika dalam situasi nyata. Contohnya, menyelesaikan masalah matematika yang berkaitan dengan kehidupan sehari-hari, atau mengerjakan proyek yang membutuhkan pemahaman konsep dan penerapan keterampilan. Evaluasi praktik dapat melibatkan observasi, portofolio, dan presentasi.

Pertanyaan Evaluasi

Pertanyaan evaluasi yang efektif dirancang untuk mengukur pemahaman siswa terhadap konsep-konsep kunci. Pertanyaan-pertanyaan ini tidak hanya menguji kemampuan menghafal, tetapi juga kemampuan berpikir kritis dan pemecahan masalah.

Bagaimana cara siswa menjelaskan konsep persamaan linear?
Bagaimana siswa menerapkan konsep persamaan linear dalam menyelesaikan masalah kontekstual?
Bagaimana siswa menganalisis grafik fungsi kuadrat?
Bagaimana siswa menggunakan teorema Pythagoras dalam menyelesaikan masalah geometri?

Contoh Soal Latihan

Contoh soal latihan dapat bervariasi sesuai dengan materi yang diajarkan. Soal-soal ini harus dirancang untuk menguji pemahaman siswa, bukan hanya kemampuan menghafal rumus.

Contoh Soal 1 (Persamaan Linear): Tentukan solusi dari persamaan 2x + 5 = 11. Jelaskan langkah-langkah penyelesaian dan interpretasikan hasilnya.
Contoh Soal 2 (Geometri): Sebuah segitiga siku-siku memiliki sisi miring sepanjang 10 cm dan salah satu sisi tegak lurus sepanjang 6 cm. Berapa panjang sisi tegak lurus yang lain? Gunakan teorema Pythagoras untuk menyelesaikan masalah ini.

Format Penilaian

Format penilaian yang terstruktur dan transparan sangat penting untuk memberikan umpan balik yang jelas kepada siswa. Format penilaian harus mencakup kriteria penilaian yang spesifik untuk setiap aspek yang dinilai.

Aspek Penilaian	Kriteria	Skor
Ketepatan Jawaban	Jawaban benar dan akurat	4
Kejelasan Langkah	Langkah-langkah penyelesaian dipaparkan dengan jelas dan logis	3
Kemampuan Analisis	Siswa mampu menganalisis dan menginterpretasikan hasil	2
Kemampuan Penerapan	Siswa mampu menerapkan konsep matematika dalam menyelesaikan masalah	1

Rubrik Penilaian

Rubrik penilaian yang rinci akan memberikan panduan yang jelas kepada guru dalam menilai berbagai jenis tugas. Rubrik ini harus mencakup deskripsi tingkat kemampuan siswa untuk setiap aspek penilaian.

Rubrik Penilaian Tugas Proyek: Rubrik ini dapat digunakan untuk menilai tugas proyek yang mengharuskan siswa menerapkan konsep matematika dalam menyelesaikan masalah kompleks. Rubrik ini dapat mempertimbangkan aspek kreativitas, kerja sama tim, dan penyajian hasil.
Rubrik Penilaian Presentasi: Rubrik ini dapat digunakan untuk menilai kemampuan siswa dalam mempresentasikan hasil analisis dan pemecahan masalah matematika secara lisan.

Penyesuaian Kurikulum Matematika Kelas 7 Semester 2

Penyesuaian kurikulum menjadi kunci untuk memastikan relevansi materi pembelajaran dengan kebutuhan siswa modern. Artikel ini menyajikan panduan rinci untuk mengidentifikasi materi yang perlu diubah, metode motivasi, pengembangan kreativitas, referensi tambahan, dan strategi menumbuhkan minat belajar pada mata pelajaran matematika kelas 7 semester 2.

Identifikasi Materi yang Perlu Disesuaikan

Beberapa materi dalam kurikulum matematika kelas 7 semester 2 mungkin perlu penyesuaian agar lebih relevan dengan kebutuhan siswa modern. Identifikasi materi yang perlu diubah dapat dilakukan dengan menganalisis tingkat pemahaman siswa saat ini, keterkaitan materi dengan kehidupan nyata, dan relevansi dengan perkembangan teknologi.

Materi 1: Persamaan Linear Dua Variabel (PLDV). Alasan penyesuaian: Materi ini seringkali dianggap abstrak dan sulit dipahami siswa jika hanya diajarkan secara teoritis. Alternatif pengganti: Memasukkan contoh-contoh kasus nyata dari kehidupan sehari-hari, seperti perencanaan keuangan atau perbandingan harga produk.
Materi 2: Teorema Pythagoras. Alasan penyesuaian: Penggunaan rumus tanpa pemahaman konseptual seringkali membuat siswa kesulitan dalam mengaplikasikannya dalam soal cerita. Alternatif pengganti: Mengaitkan teorema Pythagoras dengan konsep bangun datar, dan memberikan kesempatan kepada siswa untuk melakukan eksperimen atau demonstrasi langsung untuk memahami konsep tersebut.
Materi 3: Bangun Ruang Sisi Datar. Alasan penyesuaian: Materi ini cenderung bersifat kaku dan kurang melibatkan interaksi langsung. Alternatif pengganti: Memberikan aktivitas yang melibatkan visualisasi 3 dimensi, seperti membuat model bangun ruang atau menggunakan software geometri interaktif.

Metode Memotivasi Siswa

Motivasi siswa merupakan hal krusial dalam proses pembelajaran. Metode-metode berikut terbukti efektif dalam memotivasi siswa, dan dapat diterapkan dalam pembelajaran matematika kelas 7 semester 2.

Pembelajaran Berbasis Proyek: Siswa terlibat dalam proyek yang relevan dengan materi, sehingga pembelajaran menjadi lebih bermakna. Contoh: Siswa bekerja dalam kelompok untuk merancang dan membangun model jembatan yang kuat.
Penggunaan Media Interaktif: Media interaktif seperti video dan game dapat membuat pembelajaran lebih menarik dan mudah dipahami. Contoh: Menggunakan aplikasi matematika interaktif untuk melatih pemahaman konsep.
Penghargaan dan Pujian: Memberikan penghargaan dan pujian atas usaha dan prestasi siswa dapat meningkatkan motivasi belajar. Contoh: Memberikan sertifikat kepada siswa yang aktif dalam diskusi kelas.
Kerja Sama dan Kolaborasi: Memfasilitasi kerja sama dan kolaborasi dalam kelompok dapat meningkatkan partisipasi siswa. Contoh: Siswa mengerjakan soal-soal matematika dalam kelompok dan saling membantu.
Kompetisi Sehat: Membangun kompetisi sehat dapat mendorong siswa untuk lebih giat belajar. Contoh: Menerapkan sistem poin untuk setiap aktivitas yang dilakukan.

Saran untuk Mengembangkan Kreativitas Siswa

Kreativitas siswa dapat dikembangkan melalui aktivitas yang menantang dan mengasah kemampuan berpikir kritis. Berikut beberapa saran untuk mengembangkan kreativitas siswa.

Pembelajaran Berbasis Masalah: Siswa diberi masalah yang menantang untuk diselesaikan secara kreatif. Contoh: Memberikan kasus nyata tentang penerapan matematika dalam kehidupan sehari-hari dan meminta siswa mencari solusinya.
Aktivitas Penemuan: Siswa diberi kesempatan untuk menemukan konsep matematika sendiri. Contoh: Memberikan beberapa contoh soal dan meminta siswa untuk menemukan pola atau rumus yang berlaku.
Pengembangan Produk: Siswa membuat produk kreatif yang menerapkan konsep matematika. Contoh: Siswa membuat presentasi atau video pembelajaran mengenai konsep matematika yang telah dipelajari.

Referensi Tambahan

Referensi tambahan yang relevan dengan materi matematika kelas 7 semester 2 dapat memperkaya pemahaman siswa. Berikut beberapa referensi yang dapat digunakan.

Buku teks matematika kelas 7 semester 2 (nama buku)
Artikel tentang penerapan matematika dalam kehidupan sehari-hari (nama jurnal)
Website edukasi matematika (nama website)
Video pembelajaran matematika (nama platform)
Buku referensi tentang metode pembelajaran aktif (nama buku)

Strategi Menumbuhkan Minat Belajar

Minat belajar siswa dapat ditingkatkan dengan strategi yang fokus pada interaksi dan relevansi materi dengan kehidupan sehari-hari.

Pembelajaran Berbasis Pertanyaan: Memulai pembelajaran dengan pertanyaan-pertanyaan yang menarik dan relevan dengan kehidupan siswa dapat meningkatkan minat mereka. Contoh: Memulai pelajaran dengan pertanyaan seperti “Bagaimana matematika dapat membantu kita dalam menyelesaikan masalah sehari-hari?”
Aktivitas Berkelompok: Membuat pembelajaran lebih interaktif dengan aktivitas berkelompok, seperti diskusi dan kerja sama. Contoh: Menyusun kegiatan pembelajaran yang melibatkan diskusi kelompok dan presentasi hasil diskusi.
Aplikasi Matematika dalam Kehidupan Nyata: Mengaitkan konsep matematika dengan contoh-contoh dari kehidupan nyata untuk memperjelas relevansi materi. Contoh: Memberikan contoh kasus yang berkaitan dengan penggunaan persamaan linear dalam perdagangan.

Penggunaan Teknologi dalam Pembelajaran Matematika Kelas 7

Teknologi telah merevolusi cara kita belajar dan mengajar. Penggunaan teknologi dalam pembelajaran matematika kelas 7 dapat meningkatkan pemahaman dan minat siswa. Integrasi teknologi yang tepat dapat membuat pembelajaran matematika lebih interaktif, visual, dan menyenangkan.

Alat Bantu Teknologi

Beragam alat bantu teknologi dapat memperkaya pembelajaran matematika. Komputer, tablet, dan smartphone dengan aplikasi pembelajaran matematika yang interaktif dapat digunakan. Proyektor dan papan tulis interaktif juga dapat memfasilitasi demonstrasi konsep dan latihan soal secara visual.

Komputer/Laptop: Membuka akses ke berbagai sumber daya online, aplikasi interaktif, dan simulasi.
Tablet/Smartphone: Mudah dibawa dan menyediakan akses aplikasi pembelajaran matematika yang praktis dan interaktif.
Proyektor: Memudahkan penyampaian materi secara visual dan interaktif, serta mempresentasikan grafik dan diagram.
Papan Tulis Interaktif (Interactive Whiteboard): Memungkinkan interaksi langsung dengan materi, memungkinkan siswa berpartisipasi aktif dalam pembelajaran.

Aplikasi Pembelajaran Matematika

Beberapa aplikasi yang mendukung pembelajaran matematika kelas 7 meliputi aplikasi geometri interaktif, aplikasi aljabar yang memudahkan pemahaman persamaan, dan aplikasi kalkulator grafis yang membantu dalam visualisasi grafik fungsi.

GeoGebra: Aplikasi matematika dinamis yang memungkinkan siswa untuk mengeksplorasi konsep geometri, aljabar, dan kalkulus secara interaktif. Siswa dapat membuat grafik, menggambar bangun datar, dan memanipulasi objek secara langsung. Panduan pengguna dan tutorial tersedia online.
Photomath: Aplikasi yang membantu siswa menyelesaikan soal matematika dengan cara mengambil gambar soal. Aplikasi ini dapat memberikan langkah-langkah penyelesaian dan penjelasan yang membantu siswa memahami konsep.
Khan Academy: Sumber daya online yang komprehensif, termasuk video pembelajaran, latihan soal, dan materi tambahan. Khan Academy menyediakan konten matematika untuk berbagai tingkatan, termasuk untuk kelas 7.

Panduan Singkat Penggunaan Aplikasi

Untuk menggunakan aplikasi GeoGebra, siswa dapat mengunduh aplikasi tersebut dan memulai dengan tutorial dasar. Dengan aplikasi ini, siswa dapat membuat grafik fungsi, membangun bangun datar, dan memanipulasi objek secara langsung. Langkah-langkah penggunaan aplikasi GeoGebra dapat ditemukan di situs web resminya.

Aplikasi Photomath dapat digunakan dengan mengambil gambar soal matematika. Aplikasi akan menganalisis gambar dan memberikan langkah-langkah penyelesaian secara rinci. Siswa dapat mempelajari dan memahami cara penyelesaian soal secara bertahap.

Sumber Daya Online Relevan

Beberapa situs web dan platform online menyediakan sumber daya pembelajaran matematika yang relevan dengan materi kelas 7, seperti materi latihan soal, video pembelajaran, dan simulasi. Contohnya adalah situs web resmi Kementerian Pendidikan dan Kebudayaan.

Situs web Kementerian Pendidikan dan Kebudayaan: Memiliki sumber daya dan materi pembelajaran yang terstruktur untuk berbagai mata pelajaran, termasuk matematika.
Situs web Matematika Online: Memiliki kumpulan soal latihan, contoh soal, dan penjelasan konsep matematika.
YouTube Channel Edukasi: Memiliki video pembelajaran matematika yang informatif dan interaktif.

Skenario Pembelajaran Terintegrasi Teknologi

Skenario pembelajaran dapat dirancang dengan melibatkan penggunaan aplikasi GeoGebra untuk visualisasi konsep geometri. Siswa dapat bekerja secara berkelompok untuk membangun bangun datar dan mengeksplorasi sifat-sifatnya. Guru dapat menggunakan proyektor untuk mempresentasikan konsep aljabar secara visual, dan kemudian siswa dapat berlatih dengan aplikasi Photomath untuk menyelesaikan soal aljabar. Pembelajaran dapat diakhiri dengan diskusi kelas dan evaluasi materi.

Strategi Pembelajaran Matematika Kelas 7 Semester 2

Penguasaan strategi pembelajaran yang tepat sangat krusial untuk mencapai hasil belajar yang optimal pada siswa kelas 7 semester 2. Strategi yang efektif tidak hanya menyampaikan materi, tetapi juga mendorong pemahaman mendalam dan penerapan konsep matematika dalam kehidupan sehari-hari. Artikel ini akan membahas berbagai metode pembelajaran, contoh penerapan, dan cara meningkatkan pemahaman siswa.

Metode Pembelajaran

Penerapan beragam metode pembelajaran sangat penting untuk menciptakan suasana belajar yang dinamis dan menarik bagi siswa. Metode-metode ini akan dijelaskan secara rinci, dengan contoh penerapannya dalam konteks pembelajaran matematika.

Pembelajaran Berbasis Masalah (Problem-Based Learning): Metode ini mendorong siswa untuk memecahkan masalah nyata. Guru dapat mengajukan pertanyaan yang menantang dan mendorong siswa untuk mencari solusi, dengan demikian siswa dapat mengembangkan keterampilan berpikir kritis. Contohnya, dalam mempelajari persamaan linear, guru dapat memberikan kasus tentang pembagian tugas dalam proyek kelompok.
Pembelajaran Kolaboratif: Metode ini mendorong kerja sama dan interaksi antar siswa. Guru dapat membagi siswa ke dalam kelompok kecil untuk menyelesaikan tugas bersama. Contohnya, dalam mempelajari materi geometri, siswa dapat bekerja sama untuk mengukur dan menghitung luas bangun datar.
Pembelajaran Berbasis Proyek: Metode ini mendorong siswa untuk menyelesaikan proyek yang menantang. Proyek ini dapat berkaitan dengan penerapan konsep matematika dalam kehidupan nyata. Contohnya, siswa dapat membuat model bangun ruang dan menghitung volumenya.
Pembelajaran Berbasis Kasus: Metode ini mendorong siswa untuk menganalisis kasus nyata dan mencari solusi menggunakan konsep matematika. Contohnya, dalam mempelajari persentase, guru dapat memberikan kasus tentang diskon barang di toko.
Pembelajaran Tematik: Metode ini menghubungkan materi matematika dengan tema tertentu. Contohnya, dalam mempelajari pengukuran, guru dapat menghubungkannya dengan tema tentang pembangunan rumah.

Deskripsi Singkat Metode Pembelajaran

Pemahaman mendalam tentang cara kerja dan efektifitas setiap metode pembelajaran akan meningkatkan implementasinya di kelas. Berikut penjelasan lebih rinci:

Pembelajaran Berbasis Masalah: Metode ini efektif untuk mengembangkan kemampuan berpikir kritis dan pemecahan masalah siswa. Metode ini cocok diterapkan ketika guru ingin mendorong siswa untuk menemukan jawaban sendiri berdasarkan masalah yang diberikan. Contohnya, dalam pembelajaran tentang bangun datar, guru bisa mengajukan pertanyaan “Bagaimana kita bisa menghitung luas taman yang berbentuk trapesium?”.

Contoh Penerapan Metode Pembelajaran

Penerapan metode pembelajaran yang tepat dalam konteks yang spesifik akan menghasilkan hasil belajar yang lebih baik. Berikut contoh penerapannya:

Pembelajaran Kolaboratif untuk Persamaan Linear Dua Variabel: Siswa dibagi ke dalam kelompok 4 orang. Setiap kelompok diberikan soal-soal persamaan linear dua variabel yang berbeda. Guru memantau interaksi antar siswa dalam kelompok, memastikan setiap siswa terlibat dalam proses pemecahan masalah. Tugas kelompok dapat berupa presentasi hasil dan diskusi kelompok.

Meningkatkan Pemahaman Siswa

Strategi untuk meningkatkan pemahaman siswa meliputi pemberian umpan balik yang konstruktif, penggunaan beragam media pembelajaran, dan penciptaan suasana belajar yang mendukung.

Umpan Balik Konstruktif: Guru memberikan umpan balik yang spesifik dan terarah kepada siswa, fokus pada proses berpikir dan langkah-langkah yang dilakukan. Contohnya, saat siswa mengerjakan soal cerita matematika, guru dapat memberikan umpan balik terkait pemahaman konsep, penyusunan langkah-langkah, dan penggunaan operasi matematika yang tepat.

Aktivitas Pembelajaran Interaktif

Aktivitas pembelajaran interaktif dirancang untuk meningkatkan partisipasi siswa dan memperkuat pemahaman mereka.

Aktivitas Pembelajaran: Siswa dibagi menjadi kelompok kecil. Setiap kelompok diberi tugas untuk membuat presentasi sederhana tentang aplikasi persamaan linear dalam kehidupan sehari-hari. Presentasi ini dapat berupa video pendek, poster, atau demonstrasi sederhana. Guru memfasilitasi diskusi dan presentasi antar kelompok.

Contoh Rencana Pelaksanaan Pembelajaran (RPP)

Rencana Pelaksanaan Pembelajaran (RPP) berikut ini disusun sebagai contoh untuk mata pelajaran Matematika kelas VII SMP semester 1, dengan tema Operasi Hitung Bilangan Bulat. RPP ini didasarkan pada asumsi bahwa silabus yang relevan tersedia dan digunakan sebagai acuan.

Tujuan Pembelajaran

Siswa mampu memahami dan menerapkan operasi hitung bilangan bulat dengan tepat. Berikut beberapa tujuan pembelajaran spesifik dan terukur:

Siswa dapat mendefinisikan operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan bulat dengan benar.
Siswa dapat menyelesaikan operasi penjumlahan bilangan bulat positif dan negatif dengan minimal 80% benar.
Siswa dapat menerapkan aturan operasi hitung campuran bilangan bulat dengan tepat.

Materi Pembelajaran

Materi pembelajaran meliputi operasi hitung bilangan bulat, termasuk penjumlahan, pengurangan, perkalian, dan pembagian. Materi ini difokuskan pada pemahaman konsep dan penerapannya.

Metode Pembelajaran

Metode pembelajaran yang digunakan dalam RPP ini meliputi diskusi kelompok, tanya jawab, demonstrasi, dan penugasan individu.

Kegiatan Pembelajaran

Kegiatan pembelajaran dibagi menjadi tiga bagian: Pendahuluan, Kegiatan Inti, dan Penutup.

Pendahuluan

Dalam pendahuluan, guru akan melakukan apersepsi dengan mengingat kembali materi operasi hitung bilangan cacah. Guru juga memotivasi siswa untuk mempelajari operasi hitung bilangan bulat dengan memberikan konteks kehidupan sehari-hari. Alokasi waktu: 10 menit.

Kegiatan Inti

Kegiatan inti terdiri dari minimal tiga aktivitas, yang diuraikan dalam tabel berikut:

No	Waktu	Kegiatan	Materi	Metode	Media
1	15 menit	Aktivitas 1: Diskusi kelompok tentang aturan penjumlahan bilangan bulat.	Operasi penjumlahan bilangan bulat	Diskusi kelompok	Lembar kerja, spidol, papan tulis
2	15 menit	Aktivitas 2: Demonstrasi penyelesaian soal operasi pengurangan bilangan bulat oleh guru.	Operasi pengurangan bilangan bulat	Demonstrasi	Papan tulis, spidol
3	20 menit	Aktivitas 3: Latihan soal operasi perkalian dan pembagian bilangan bulat dalam kelompok.	Operasi perkalian dan pembagian bilangan bulat	Diskusi kelompok, tanya jawab	Lembar kerja, spidol, papan tulis

Penutup

Dalam penutup, guru akan melakukan refleksi bersama siswa terkait materi yang telah dipelajari. Guru juga memberikan evaluasi singkat dan memberikan penugasan untuk pertemuan berikutnya. Alokasi waktu: 15 menit.

Penilaian

Penilaian dilakukan melalui beberapa cara, meliputi penilaian lisan, tertulis, dan portofolio.

Penilaian lisan: Menilai pemahaman siswa melalui tanya jawab selama diskusi.
Penilaian tertulis: Menggunakan lembar kerja dan soal-soal pilihan ganda dan uraian untuk mengukur pemahaman konsep.
Portofolio: Mengumpulkan hasil pekerjaan siswa sebagai bukti proses belajar.

Contoh Penugasan

Pertemuan 1: Siswa mengerjakan 5 soal pilihan ganda dan 3 soal uraian tentang operasi penjumlahan bilangan bulat. (Contoh soal dan kunci jawaban dilampirkan).
Pertemuan 2: Siswa mengerjakan soal-soal operasi pengurangan, perkalian, dan pembagian bilangan bulat.

Referensi Tambahan

Pemahaman yang mendalam tentang materi matematika kelas 7 semester 2 tidak hanya bergantung pada silabus yang ada. Referensi tambahan dari berbagai sumber sangat penting untuk memperkaya pemahaman dan memberikan perspektif yang lebih luas. Referensi ini dapat berupa buku, situs web, jurnal, atau sumber daya lainnya yang dapat diakses oleh guru dan siswa.

Daftar Buku Referensi

Buku referensi matematika untuk kelas 7 semester 2 dapat memberikan contoh soal, penjelasan konsep, dan latihan yang bervariasi. Beberapa penerbit buku teks yang terkemuka, seperti Erlangga, Penerbit Kemdikbud, dan Gramedia, menawarkan buku-buku yang sesuai dengan kurikulum 2013. Buku-buku ini biasanya mencakup materi-materi yang terkait dengan aljabar dasar, geometri, dan statistika. Penting untuk memilih buku referensi yang sesuai dengan kebutuhan dan gaya belajar siswa.

Buku Matematika SMP Kelas 7 Semester 2 (Penerbit X)
Buku Panduan Guru Matematika SMP Kelas 7 Semester 2 (Penerbit Y)
Ensiklopedia Matematika untuk Pemula

Sumber Daya Online

Akses ke internet membuka pintu menuju berbagai sumber daya online yang berharga. Situs web pendidikan, forum diskusi, dan video pembelajaran dapat memberikan penjelasan tambahan dan contoh soal yang lebih interaktif. Penting untuk memastikan sumber online tersebut kredibel dan relevan dengan kurikulum 2013.

Situs web Kemdikbud
Situs web sekolah atau lembaga pendidikan
Platform pembelajaran daring seperti Khan Academy dan YouTube Education

Jurnal dan Artikel Terkait

Jurnal dan artikel ilmiah dapat memberikan wawasan lebih mendalam tentang perkembangan dan inovasi dalam pembelajaran matematika. Informasi ini dapat digunakan untuk mengembangkan strategi pembelajaran yang lebih efektif dan kreatif.

Jurnal Pendidikan Matematika
Jurnal penelitian terkait penerapan pembelajaran matematika di tingkat SMP
Artikel di blog atau website pendidikan matematika

Sumber Daya Guru dan Siswa

Sumber daya yang diakses oleh guru dan siswa harus mencakup berbagai macam media, termasuk buku, situs web, jurnal, dan sumber daya lainnya. Pilihan yang beragam dapat memberikan perspektif yang lebih luas tentang konsep matematika dan memperkaya pembelajaran.

Kategori	Contoh Sumber Daya
Buku Teks	Buku Matematika SMP Kelas 7 Semester 2
Situs Web	Situs web Kemdikbud, Khan Academy
Jurnal	Jurnal Pendidikan Matematika
Aplikasi	Aplikasi pembelajaran matematika

Ringkasan Referensi

Referensi tambahan yang beragam dapat memberikan pemahaman yang komprehensif dan menyeluruh tentang materi matematika kelas 7 semester 2. Buku referensi menyediakan contoh soal dan penjelasan yang terstruktur. Sumber daya online menawarkan pendekatan pembelajaran yang lebih interaktif dan beragam. Jurnal dan artikel terkait memberikan wawasan terkini tentang perkembangan pembelajaran matematika. Dengan menggabungkan berbagai referensi ini, guru dan siswa dapat memperkaya pemahaman dan keterampilan matematika mereka.

Keterkaitan dengan Materi Sebelumnya

Memahami materi matematika kelas 7 semester 2 tidak bisa dilepaskan dari pemahaman materi semester 1. Keterkaitan ini penting untuk membangun pemahaman yang utuh dan kokoh. Semester 2 akan mengelaborasi konsep-konsep dasar yang telah dipelajari sebelumnya dan memperluasnya dengan materi yang lebih kompleks.

Hubungan Materi Semester 1 dan 2

Semester 1 kelas 7 biasanya mencakup materi dasar seperti bilangan bulat, pecahan, dan pengukuran. Semester 2 akan menggabungkan dan memperluas pemahaman ini dengan konsep aljabar, geometri, dan peluang. Contohnya, pemahaman tentang operasi bilangan bulat akan sangat membantu dalam menyelesaikan persamaan linear sederhana.

Konsep Penting yang Diperkuat

Operasi Hitung Bilangan Bulat dan Pecahan: Kemampuan dalam melakukan operasi hitung bilangan bulat dan pecahan merupakan pondasi penting dalam menyelesaikan soal-soal aljabar dan geometri. Kemampuan ini akan terus dipraktikkan dan diperluas dalam konteks yang lebih kompleks.
Pengukuran dan Geometri Dasar: Pemahaman tentang satuan pengukuran dan bangun datar dasar seperti persegi, persegi panjang, dan segitiga akan menjadi kunci dalam memahami konsep luas dan volume pada semester 2.
Data dan Representasi Data: Pengolahan dan interpretasi data yang telah dipelajari di semester 1 akan menjadi dasar untuk memahami peluang dan statistik pada semester 2. Kemampuan dalam membaca dan menganalisis data akan sangat membantu.

Peta Konsep Keterkaitan Materi

Peta konsep dapat digambarkan sebagai sebuah diagram yang menunjukkan hubungan antar topik. Misalnya, lingkaran besar yang berisi “Matematika Kelas 7 Semester 2” terhubung dengan lingkaran-lingkaran lebih kecil yang mewakili “Aljabar”, “Geometri”, dan “Peluang”. Lingkaran-lingkaran kecil ini juga terhubung dengan garis ke lingkaran-lingkaran yang lebih kecil lagi yang mewakili konsep-konsep penting seperti “Persamaan Linear”, “Bangun Ruang”, dan “Peluang Kombinasi”.

Tabel Perbandingan Materi Semester 1 dan 2

Semester 1	Semester 2	Keterkaitan
Bilangan Bulat	Persamaan Linear	Operasi bilangan bulat menjadi dasar untuk menyelesaikan persamaan linear.
Pecahan	Perbandingan dan Skala	Pemahaman pecahan membantu dalam memahami perbandingan dan skala.
Bangun Datar	Bangun Ruang	Pemahaman bangun datar akan membantu dalam memahami bangun ruang.
Data dan Grafik	Peluang	Pengolahan data di semester 1 membantu dalam memahami konsep peluang.

Topik Pondasi untuk Pemahaman Semester 2

Beberapa topik di semester 1 akan menjadi pondasi kuat untuk memahami materi semester 2. Pemahaman yang baik tentang operasi bilangan, pengukuran, dan geometri dasar merupakan kunci sukses dalam mempelajari konsep-konsep yang lebih kompleks di semester 2. Misalnya, konsep perbandingan dan proporsi erat kaitannya dengan konsep pecahan yang dipelajari di semester 1.

Penerapan Konsep dalam Kehidupan Sehari-hari: Silabus Matematika Kelas 7 Semester 2 Kurikulum 2013

Matematika, seringkali dianggap sebagai subjek yang abstrak dan rumit, nyatanya memiliki peran mendasar dan tak terpisahkan dalam kehidupan sehari-hari. Dari perhitungan sederhana hingga permodelan kompleks, penerapan matematika memandu berbagai aspek kehidupan kita, mulai dari pengambilan keputusan finansial hingga pemahaman fenomena alam. Artikel ini akan mengupas beberapa contoh nyata bagaimana konsep matematika diimplementasikan dalam kegiatan sehari-hari.

Contoh Penerapan Matematika dalam Kehidupan Sehari-hari

Berikut beberapa contoh penerapan matematika dalam kehidupan sehari-hari, dengan penekanan pada penerapan konsep-konsep yang spesifik dan terukur.

Perhitungan Diskon dan Promosi: Misalnya, menghitung diskon 20% dari harga barang Rp 100.000. Penerapan matematika di sini adalah melalui konsep persentase. Rumus persentase digunakan untuk menentukan nilai diskon, dan perhitungan sederhana menghasilkan nilai diskon sebesar Rp 20.000. Ini adalah penerapan aljabar yang praktis dalam aktivitas belanja.
Pengukuran dan Perencanaan Ruangan: Dalam merencanakan renovasi rumah, misalnya, diperlukan perhitungan luas ruangan. Konsep geometri, khususnya rumus luas persegi panjang, sangat penting. Misalnya, menghitung luas sebuah kamar tidur berukuran 3 meter x 4 meter. Penerapan rumus luas persegi panjang (panjang x lebar) menghasilkan luas 12 meter persegi. Perhitungan ini sangat vital untuk menentukan jumlah material yang dibutuhkan.
Perencanaan Keuangan dan Investasi: Dalam merencanakan tabungan untuk masa depan, kita memerlukan perhitungan bunga. Konsep bunga majemuk merupakan penerapan aljabar dalam investasi. Misalnya, jika seseorang menabung Rp 1.000.000 dengan bunga 5% per tahun, maka perhitungan bunga majemuk akan menunjukkan jumlah tabungan yang akan diperoleh setelah beberapa tahun. Perhitungan ini juga berlaku untuk menghitung kredit atau pinjaman.

Ilustrasi Penerapan Konsep

Berikut beberapa ilustrasi sederhana untuk memperjelas penerapan konsep matematika yang telah disebutkan.

Perhitungan Diskon: Ilustrasi sederhana bisa berupa gambar sebuah produk dengan harga Rp 100.000, dan terdapat label diskon 20%. Gambar tersebut dapat disertai dengan perhitungan matematika yang menunjukkan bagaimana diskon tersebut dihitung.
Pengukuran Ruangan: Gambarkan sebuah ruangan dengan ukuran yang terukur. Tambahkan keterangan mengenai panjang dan lebar ruangan. Gambarkan rumus luas persegi panjang yang digunakan untuk menghitung luas ruangan.
Perencanaan Keuangan: Diagram batang dapat digunakan untuk memperlihatkan perkiraan tabungan di masa depan. Grafik ini memperlihatkan bagaimana tabungan meningkat seiring waktu dengan perhitungan bunga majemuk.

Permasalahan Kehidupan Nyata

Berikut contoh permasalahan kehidupan nyata yang dapat diselesaikan dengan penerapan konsep matematika.

Pembelian Bahan Makanan: Seorang ibu ingin membeli 3 kg apel dan 2 kg jeruk. Harga apel Rp 20.000/kg dan jeruk Rp 15.000/kg. Berapa total yang harus dibayarkan? Perhitungan ini melibatkan operasi penjumlahan dan perkalian.
Keuntungan Penjualan: Seorang pedagang ingin mengetahui berapa keuntungan yang diperoleh jika ia menjual 50 buah mangga dengan harga Rp 5.000 per buah dan biaya pembelian mangga Rp 200.000. Perhitungan ini melibatkan operasi pengurangan untuk menghitung keuntungan.

Silabus matematika kelas 7 semester 2 kurikulum 2013, menarik bukan? Namun, tahukah Anda bahwa beberapa konsep matematika, seperti probabilitas dan statistik, bisa dikaitkan dengan peluang seseorang mewarisi penyakit tertentu? Seperti yang dijelaskan di penyakit yang dapat diturunkan pada keturunannya adalah , pemahaman tentang genetika dan pewarisan sifat dapat dianalogikan dengan mempelajari pola-pola dalam matematika. Dengan memahami konsep-konsep ini, kita bisa lebih terampil dalam mengaplikasikannya dalam kehidupan sehari-hari, termasuk dalam silabus matematika kelas 7 semester 2 kurikulum 2013 itu sendiri.

Aplikasi Matematika dalam Berbagai Bidang

Penerapan matematika tak terbatas pada contoh-contoh sederhana di atas. Matematika berperan penting dalam berbagai bidang, seperti:

Bisnis: Matematika digunakan untuk menganalisis tren pasar, memprediksi permintaan, dan mengoptimalkan strategi pemasaran.
Teknik: Dalam perancangan jembatan, bangunan, dan mesin, matematika berperan penting dalam perhitungan kekuatan dan stabilitas.
Kesehatan: Matematika digunakan dalam pemodelan penyakit, perancangan obat, dan pengolahan data medis.

Pemetaan Kompetensi dalam Silabus Matematika Kelas 7 Semester 2

Pemetaan kompetensi merupakan langkah krusial dalam pengembangan silabus. Dengan pemetaan yang terstruktur, guru dapat memahami secara menyeluruh capaian pembelajaran yang diharapkan. Hal ini memungkinkan perencanaan pembelajaran yang lebih efektif dan evaluasi yang terarah.

Bagan Pemetaan Kompetensi

Diagram pemetaan kompetensi memvisualisasikan hubungan hierarkis antara Kompetensi Inti (KI), Kompetensi Dasar (KD), dan Indikator Pencapaian Kompetensi (IPK). Diagram yang jelas, seperti diagram Venn atau diagram pohon, akan membantu memahami keterkaitan antar level kompetensi. Penggunaan warna dan simbol yang berbeda akan mempermudah membedakan level kompetensi.

Diagram Venn akan menunjukkan irisan antara KI, KD, dan IPK, memperlihatkan aspek-aspek yang saling terkait.
Diagram pohon akan menampilkan struktur hierarki, mulai dari KI yang lebih umum hingga IPK yang spesifik.
Pemilihan diagram tergantung pada fokus dan tingkat detail yang diinginkan dalam pemetaan.

Identifikasi Kompetensi Inti dan Kompetensi Dasar

Identifikasi KI dan KD yang relevan dengan silabus matematika kelas 7 semester 2 harus dilakukan secara akurat. Penomoran KI dan KD mengikuti standar yang berlaku.

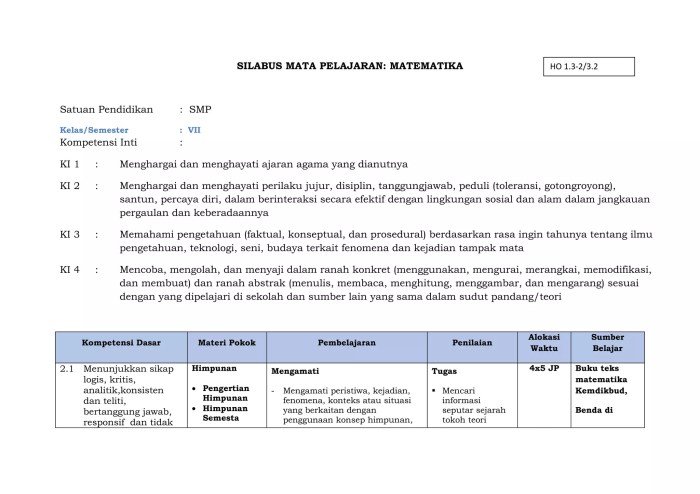
No KI/KD	Deskripsi KI/KD	Referensi dalam Silabus
KI 3.1	Memahami konsep bilangan bulat dan pecahan serta operasinya.	Bab 1, halaman 5-10
KD 4.1	Menerapkan operasi hitung bilangan bulat dan pecahan dalam pemecahan masalah kontekstual.	Bab 1, halaman 11-15

Deskripsi Kompetensi

Deskripsi rinci untuk setiap KI dan KD menjelaskan kompetensi tersebut secara lugas dan menghindari jargon. Deskripsi juga mencakup contoh penerapan dalam konteks nyata, keterkaitan dengan aspek pengetahuan, keterampilan, dan sikap, serta tingkat kesulitan.

No KI/KD	Deskripsi KI/KD	Contoh Penerapan	Aspek (Pengetahuan, Keterampilan, Sikap)	Tingkat Kesulitan
KI 3.1	Memahami konsep bilangan bulat dan pecahan serta operasinya.	Menghitung keuntungan/kerugian dalam jual beli.	Pengetahuan, Keterampilan	Sedang

Indikator Pencapaian Kompetensi

Indikator Pencapaian Kompetensi (IPK) untuk setiap KD memberikan gambaran spesifik tentang apa yang harus dikuasai siswa. IPK dirumuskan secara terukur dan dapat diamati, dilengkapi dengan contoh kegiatan/aktivitas untuk mengukurnya. Level kompetensi, seperti memahami, menerapkan, menganalisis, mengevaluasi, dan mencipta, juga dicantumkan.

No KD	No IPK	Deskripsi IPK	Contoh Kegiatan	Level Kompetensi
KD 4.1	IPK 1	Menyelesaikan soal cerita tentang operasi hitung bilangan bulat.	Latihan soal, diskusi kelompok	Menerapkan

Diagram Pohon Hierarki Kompetensi

Diagram pohon menggambarkan hierarki kompetensi, mulai dari KI hingga IPK. Diagram ini memperlihatkan hubungan sebab-akibat antar level kompetensi. Contoh: KI 3.4 bercabang ke KD 3.4.1 dan IPK terkait.

(Ilustrasi diagram pohon di sini akan sangat membantu, tetapi tidak ada tag image/gambar yang diizinkan)

Penulisan Teks Pendukung

Teks pendukung memberikan ringkasan dan interpretasi dari pemetaan kompetensi. Dijelaskan bagaimana pemetaan ini digunakan untuk perencanaan pembelajaran dan evaluasi. Sumber silabus juga harus dirujuk.

(Contoh teks pendukung: Pemetaan ini menunjukkan bagaimana kompetensi inti dalam silabus matematika kelas 7 semester 2 terjabar menjadi kompetensi dasar yang spesifik dan indikator pencapaian yang terukur. Hal ini akan membantu guru dalam menyusun RPP dan mengevaluasi pencapaian pembelajaran siswa. Silabus Matematika Kelas 7 Semester 2, Penerbit X, 2023.)

Pengembangan Keterampilan Berpikir Kritis

Silabus matematika kelas 7 semester 2 kurikulum 2013

Source: slidesharecdn.com

Keterampilan berpikir kritis merupakan kunci sukses dalam pembelajaran matematika. Artikel ini membahas cara mengembangkan keterampilan tersebut pada siswa kelas 7 melalui contoh soal, strategi, dan aktivitas pembelajaran yang terstruktur.

Contoh Soal yang Mendorong Berpikir Kritis

Contoh soal yang dirancang untuk mendorong berpikir kritis harus menantang siswa untuk menganalisis informasi, mengevaluasi argumen, dan mensintesis ide. Berikut beberapa contoh soal dengan tingkat kesulitan yang berbeda.

Contoh Soal (Mudah):
- Judul/Topik: Operasi Hitung Bilangan Bulat
- Pertanyaan: Jika suhu di pagi hari 15°C dan suhu menurun 8°C di siang hari, berapa suhu di siang hari?
- Sumber Informasi (jika ada): Tidak ada
- Kunci Jawaban: 7°C
Contoh Soal (Sedang):
- Judul/Topik: Perbandingan dan Skala
- Pertanyaan: Sebuah peta menggunakan skala 1:50.000. Jika jarak antara dua kota pada peta adalah 5 cm, berapa jarak sebenarnya antara kedua kota tersebut?
- Sumber Informasi (jika ada): Skala peta
- Kunci Jawaban: 250.000 cm atau 2.500 meter
Contoh Soal (Sulit):
- Judul/Topik: Pola dan Barisan Bilangan
- Pertanyaan: Jika suatu barisan bilangan memiliki pola 2n ²
  -3n, carilah bilangan ke-10 dalam barisan tersebut dan jelaskan langkah-langkah yang dilakukan untuk menentukan pola tersebut.
- Sumber Informasi (jika ada): Rumus umum pola bilangan
- Kunci Jawaban: 187
- Contoh Jawaban (Opsional): Langkah 1: Substitusikan n = 10 ke dalam rumus pola 2n ²
  -3n. Langkah 2: Hitung hasil perhitungan.

Soal yang Menantang Analisis Informasi, Silabus matematika kelas 7 semester 2 kurikulum 2013

Soal-soal ini mengharuskan siswa untuk menganalisis data dari sumber yang diberikan. Berikut contoh soal.

Contoh Soal: Analisislah data penjualan produk A selama 3 bulan terakhir dan identifikasi tren penjualan. Jelaskan langkah-langkah yang Anda lakukan dalam menganalisis data tersebut. (Sumber data penjualan bisa berupa tabel atau grafik). Langkah analisis meliputi: 1. Memeriksa kecenderungan kenaikan atau penurunan penjualan; 2.

Mengidentifikasi faktor-faktor yang mungkin memengaruhi tren tersebut (misalnya, promosi, perubahan harga, atau tren pasar); 3. Membuat kesimpulan berdasarkan data yang ada.

Strategi Pengembangan Kemampuan Berpikir Kritis

Berikut beberapa strategi untuk mengembangkan kemampuan berpikir kritis siswa.

Strategi	Contoh Penerapan	Manfaat
Diskusi Terbimbing	Siswa berdiskusi tentang topik tertentu dengan panduan guru.	Mendorong berpikir kritis, berargumentasi, dan mendengarkan perspektif berbeda.
Pertanyaan Pemicu	Guru mengajukan pertanyaan terbuka yang mendorong siswa untuk berpikir lebih dalam.	Membantu mengidentifikasi asumsi, menganalisis informasi, dan menarik kesimpulan.
Pemecahan Masalah Terstruktur	Siswa diajarkan langkah-langkah pemecahan masalah secara sistematis.	Membantu mengidentifikasi masalah, menganalisis penyebab, dan mencari solusi efektif.

Jenis Pertanyaan yang Merangsang Berpikir Kritis

Pertanyaan yang tepat dapat mendorong kemampuan berpikir kritis. Berikut beberapa jenis pertanyaan tersebut:

Pertanyaan yang menuntut analisis: Mengapa terjadi demikian?
Pertanyaan yang menuntut evaluasi: Apakah argumen ini valid?
Pertanyaan yang menuntut sintesis: Bagaimana kita dapat menggabungkan ide-ide ini?
Pertanyaan yang menuntut prediksi: Apa yang akan terjadi selanjutnya?
Pertanyaan yang menuntut pertimbangan nilai: Apa yang lebih penting?

Aktivitas Pembelajaran untuk Menyelesaikan Masalah

Berikut contoh aktivitas pembelajaran yang menantang siswa menyelesaikan masalah.

Aktivitas 1: Menganalisis data hasil panen padi di beberapa desa untuk mengidentifikasi faktor-faktor yang memengaruhi hasil panen. Tujuan: Siswa dapat menganalisis data, mengidentifikasi faktor penyebab, dan menyusun kesimpulan. Langkah-langkah:
1. Mengumpulkan data hasil panen dari beberapa desa;
2. Menganalisis data menggunakan grafik atau tabel;
3.

Mengidentifikasi faktor-faktor yang mungkin memengaruhi hasil panen (misalnya, curah hujan, jenis pupuk, dan teknik pertanian);
4. Menyusun kesimpulan berdasarkan analisis. Sumber daya: Data hasil panen, buku referensi pertanian. Evaluasi: Diskusi kelas, presentasi hasil analisis.
Aktivitas 2: Merancang eksperimen sederhana untuk menguji pengaruh variasi intensitas cahaya terhadap pertumbuhan tanaman. Tujuan: Siswa dapat merancang, melaksanakan, dan menganalisis eksperimen sederhana. Langkah-langkah:
1. Menentukan variabel yang akan diteliti;
2. Merancang eksperimen untuk menguji pengaruh intensitas cahaya;
3.

Melakukan pengukuran dan perekaman data;
4. Menganalisis data dan menarik kesimpulan. Sumber daya: Bibit tanaman, lampu, pot, dan alat pengukur. Evaluasi: Presentasi hasil eksperimen, diskusi tentang validitas eksperimen.

Tugas Menulis

Berikut pertanyaan untuk tugas menulis esai singkat (500-750 kata) yang menunjukkan pemahaman tentang berpikir kritis.

Silabus matematika kelas 7 semester 2 kurikulum 2013, selain materi-materi dasar, juga memperkenalkan konsep-konsep yang lebih kompleks. Memahami bagaimana fungsi hukum pada dasarnya adalah, sangat penting untuk memahami konteks penerapan matematika dalam kehidupan sehari-hari. Fungsi hukum pada dasarnya adalah rangkaian aturan yang mengatur dan membentuk masyarakat, dan ini terkadang terhubung dengan rumus-rumus matematika yang kompleks.

Tentu saja, silabus ini tetap berfokus pada pengembangan pemahaman dasar siswa tentang aljabar, geometri, dan statistik, agar mereka siap menghadapi materi yang lebih kompleks di masa depan.

Bagaimana fenomena sosial tertentu (misalnya, bullying) dapat diatasi dengan menerapkan pendekatan berpikir kritis?

Evaluasi dan Refleksi Proses Pembelajaran

Evaluasi dan refleksi merupakan komponen penting dalam proses pembelajaran yang berkelanjutan. Dengan memahami dan menerapkan strategi evaluasi dan refleksi yang tepat, guru dapat mengidentifikasi kekuatan dan kelemahan pembelajaran, sehingga dapat meningkatkan kualitas pembelajaran di masa mendatang. Proses ini berfokus pada pemahaman mendalam tentang proses belajar dan hasil yang dicapai.

Saran Evaluasi Pembelajaran

Evaluasi pembelajaran yang efektif haruslah spesifik dan terukur. Menggunakan kriteria, bobot, dan rubrik penilaian yang jelas sangat penting. Evaluasi tidak hanya dilakukan pada akhir pembelajaran, tetapi juga pada setiap tahapan pembelajaran untuk mendeteksi kendala lebih dini.

Evaluasi yang spesifik, seperti penggunaan portofolio, harus dijelaskan secara rinci. Kriteria penilaian, bobot masing-masing aspek, dan contoh rubrik akan memberikan gambaran yang jelas tentang cara evaluasi tersebut.
Evaluasi harus dirancang untuk mengukur pemahaman konsep secara menyeluruh, bukan hanya hafalan. Contohnya, untuk mengukur pemahaman konsep integral kalkulus, dapat dirancang evaluasi yang mengharuskan mahasiswa menjelaskan konsep tersebut dengan kata-kata sendiri, atau menerapkan konsep tersebut dalam soal-soal terapan.
Evaluasi pada setiap tahapan pembelajaran akan membantu guru untuk mengidentifikasi permasalahan dan melakukan intervensi tepat waktu. Hal ini akan membantu siswa untuk memahami materi dengan lebih baik.

Format Refleksi Pembelajaran

Refleksi pembelajaran yang terstruktur akan membantu guru untuk menganalisis proses pembelajaran dan mengidentifikasi faktor-faktor yang mempengaruhi hasil belajar. Format yang terstruktur akan membantu guru untuk memahami aspek-aspek penting dari proses pembelajaran.

Penggunaan tabel, diagram, atau format naratif dengan kolom-kolom yang jelas sangat direkomendasikan. Kolom-kolom tersebut harus mendorong pemahaman mendalam tentang proses belajar, seperti aktivitas yang dilakukan, hambatan yang dihadapi, strategi yang digunakan untuk mengatasi hambatan, hasil yang dicapai, dan pelajaran yang dipetik.
Contoh format refleksi untuk kegiatan presentasi di kelas dapat mencakup kolom ‘Aktivitas’, ‘Hambatan’, ‘Strategi Mengatasi’, ‘Hasil’, dan ‘Pelajaran yang Dipetik’. Dengan format ini, guru dapat menganalisis faktor-faktor yang mempengaruhi keberhasilan atau kegagalan dalam presentasi.

Metode Meningkatkan Kualitas Pembelajaran

Peningkatan kualitas pembelajaran membutuhkan metode yang terukur dan praktis. Metode yang dipilih harus jelas langkah-langkahnya dan memiliki indikator keberhasilan yang terdefinisi.

Pelatihan tambahan atau workshop harus dijelaskan secara rinci bagaimana pelatihan tersebut akan dilaksanakan dan apa indikator keberhasilannya. Misalnya, untuk meningkatkan pemahaman konsep fisika klasik, pelatihan dapat dirancang dengan modul belajar interaktif, diskusi kelompok, dan sesi tanya jawab dengan tutor.
Langkah-langkah pelatihan harus terukur dan terdokumentasi. Indikator keberhasilannya harus dapat diukur, misalnya melalui peningkatan skor tes atau kemampuan siswa dalam menyelesaikan soal-soal fisika klasik.

Cara Mengevaluasi Hasil Pembelajaran

Evaluasi hasil pembelajaran haruslah objektif dan selaras dengan tujuan pembelajaran. Hasil evaluasi akan digunakan sebagai dasar untuk perbaikan pembelajaran selanjutnya.

Evaluasi hasil pembelajaran pembuatan program aplikasi sederhana dengan Python harus mencakup pemahaman konsep, kemampuan coding, dan kemampuan pemecahan masalah. Contoh pertanyaan dapat berupa soal-soal yang mengharuskan siswa untuk menjelaskan logika program, menganalisis kesalahan program, dan mengidentifikasi solusi alternatif.
Kriteria penilaian yang terukur akan membantu dalam mengevaluasi hasil pembelajaran. Rubrik penilaian yang jelas akan membantu dalam mengukur kemampuan siswa dalam setiap aspek.

Faktor Pendukung dan Penghambat

Identifikasi faktor-faktor pendukung dan penghambat proses pembelajaran sangat penting untuk pengembangan strategi pembelajaran yang lebih efektif. Faktor-faktor ini harus diidentifikasi secara spesifik, bukan hanya secara umum.

Contohnya, kurangnya waktu bukanlah faktor yang spesifik. Sebaliknya, perlu dijelaskan bagaimana kekurangan waktu tersebut memengaruhi proses pembelajaran, misalnya dengan menjelaskan bahwa waktu yang terbatas membuat guru tidak dapat memberikan penjelasan yang cukup detail pada materi tertentu. Solusi untuk mengatasi faktor penghambat haruslah terukur dan dapat diimplementasikan.
Identifikasi faktor-faktor seperti ketersediaan sumber belajar, dukungan orang tua, dan motivasi siswa harus dilakukan untuk mengoptimalkan proses pembelajaran.

Terakhir

Dengan memahami silabus matematika kelas 7 semester 2 kurikulum 2013, guru dan siswa dapat merencanakan pembelajaran dengan lebih terarah. Materi-materi yang terstruktur dan contoh-contoh penerapannya dalam kehidupan nyata akan mempermudah pemahaman. Semoga silabus ini menjadi alat yang efektif untuk meningkatkan pemahaman dan keterampilan matematika siswa.

Pertanyaan Umum (FAQ)

Bagaimana cara mendapatkan silabus lengkap?

Silabus lengkap biasanya tersedia di sekolah atau dapat diunduh dari sumber resmi Kementerian Pendidikan dan Kebudayaan.

Apa saja materi prasyarat yang harus dikuasai sebelum mempelajari semester 2?

Materi prasyarat perlu diidentifikasi dan dibahas dalam silabus. Biasanya mencakup konsep-konsep dasar seperti operasi hitung bilangan bulat, pecahan, dan pengukuran.

Apakah terdapat contoh soal dan pembahasan dalam silabus?

Silabus matematika biasanya menyertakan contoh soal dan pembahasan untuk membantu siswa memahami konsep-konsep yang diajarkan.

Bagaimana cara mengaplikasikan materi matematika dalam kehidupan sehari-hari?

Silabus matematika kelas 7 semester 2 kurikulum 2013 akan menyediakan contoh penerapan materi dalam kehidupan sehari-hari untuk mempermudah pemahaman dan motivasi belajar.

Post Views: 1