Cara Mengubah Putaran Ke Radian Panduan Lengkap Dan Aplikasinya

Pernahkah terpikir bagaimana roda berputar diukur, atau bagaimana sudut dalam animasi komputer dihitung? Jawabannya seringkali melibatkan konversi yang krusial: cara mengubah putaran ke radian. Satuan ini, mungkin terdengar asing bagi sebagian orang, memegang peranan penting dalam berbagai bidang, mulai dari matematika dasar hingga rekayasa dan animasi. Mari kita selami dunia menarik di mana putaran bertemu radian, mengungkap rahasia di balik konversi ini.

Konversi putaran ke radian adalah jembatan penting dalam matematika dan fisika. Putaran, seringkali digunakan untuk mengukur revolusi penuh, sementara radian mengukur sudut berdasarkan panjang busur lingkaran. Memahami cara mengubah putaran ke radian membuka pintu ke pemahaman yang lebih dalam tentang konsep sudut, gerakan melingkar, dan aplikasi di dunia nyata.

Table of Contents

Pengertian Dasar Putaran dan Radian

Dalam dunia matematika dan fisika, pengukuran sudut adalah konsep fundamental yang mendasari banyak aspek kehidupan kita. Dua satuan yang paling sering digunakan untuk mengukur sudut adalah putaran (revolusi) dan radian. Keduanya memiliki definisi, kegunaan, dan kelebihan serta kekurangan masing-masing. Memahami perbedaan mendasar antara keduanya sangat penting untuk menguasai konsep-konsep terkait seperti rotasi, navigasi, dan analisis gelombang.

Berbicara tentang matematika, mengubah putaran ke radian itu krusial, kan? Tapi, kadang kita juga perlu keterampilan lain, seperti saat berhadapan dengan dokumen Word. Pernahkah Anda frustrasi dengan sheet kosong yang mengganggu? Untungnya, ada solusi mudah untuk menghapus sheet kosong di Word , sehingga pekerjaan lebih efisien. Kembali ke radian, pemahaman ini penting untuk banyak perhitungan, memastikan presisi dalam berbagai bidang.

Mari kita selami lebih dalam perbedaan antara putaran dan radian.

Definisi dan Perbedaan Mendasar

Perbedaan utama antara putaran dan radian terletak pada definisi matematis dan cara mereka mengukur sudut. Mari kita bedah perbedaan tersebut:

Putaran (Revolusi): Putaran adalah satuan pengukuran sudut yang mendefinisikan satu putaran penuh sebagai satu putaran. Secara matematis, satu putaran penuh setara dengan 360 derajat.
Radian: Radian adalah satuan pengukuran sudut yang didefinisikan berdasarkan rasio panjang busur lingkaran terhadap jari-jarinya. Satu radian adalah sudut yang dibentuk ketika panjang busur sama dengan panjang jari-jari lingkaran. Satu putaran penuh setara dengan 2π radian, di mana π (pi) adalah konstanta matematika yang nilainya kira-kira 3.14159.

Hubungan antara Putaran dan Radian (Konversi):

Karena satu putaran penuh setara dengan 2π radian, kita dapat menggunakan hubungan ini untuk mengkonversi antara keduanya. Rumus konversinya adalah:

Untuk mengkonversi putaran ke radian: radian = putaran - 2π
Untuk mengkonversi radian ke putaran: putaran = radian / 2π

Kelebihan dan Kekurangan:

Putaran: Kelebihannya adalah mudah dipahami karena terkait langsung dengan konsep “putaran” atau “revolusi” yang intuitif. Kekurangannya adalah dalam perhitungan matematika, derajat seringkali kurang praktis karena tidak terkait langsung dengan sifat geometris lingkaran.
Radian: Kelebihannya adalah sangat berguna dalam kalkulus dan fisika karena terkait langsung dengan sifat geometris lingkaran (rasio busur terhadap jari-jari). Hal ini menyederhanakan banyak rumus dan perhitungan, terutama yang melibatkan fungsi trigonometri. Kekurangannya adalah mungkin kurang intuitif bagi sebagian orang karena tidak secara langsung terkait dengan konsep “putaran” sehari-hari.

Contoh Penggunaan Putaran dan Radian

Baik putaran maupun radian memiliki aplikasi yang luas dalam berbagai bidang. Berikut adalah beberapa contoh konkret:

Putaran dalam Mekanika: Dalam mekanika, putaran sering digunakan untuk mengukur kecepatan rotasi suatu objek. Misalnya, kecepatan rotasi roda mobil diukur dalam putaran per menit (RPM) atau putaran per detik (RPS).
Radian dalam Navigasi: Dalam navigasi, radian digunakan untuk menghitung sudut dalam sistem seperti GPS. Sudut diukur dalam radian untuk menghitung jarak dan arah antara titik-titik.
Radian dalam Grafik: Dalam grafik, terutama dalam fungsi trigonometri, radian digunakan untuk merepresentasikan sudut. Hal ini karena fungsi trigonometri seperti sinus dan kosinus didefinisikan berdasarkan radian.

Perbandingan Putaran dan Radian

Berikut adalah tabel yang merangkum perbedaan utama antara putaran dan radian:

Kolom	Definisi	Simbol	Satuan Turunan	Rumus Konversi	Contoh Penggunaan
Definisi	Satu putaran penuh adalah satu putaran. Satu putaran penuh setara dengan 360 derajat.	put atau rev	RPM (putaran per menit), RPS (putaran per detik), Hz (Hertz, untuk frekuensi)	Radian = putaran 2π Contoh 0.5 putaran = 0.5 – 2π = π radian	Kecepatan rotasi roda, kecepatan mesin
Definisi	Satu radian adalah sudut yang dibentuk ketika panjang busur lingkaran sama dengan panjang jari-jari lingkaran. Satu putaran penuh setara dengan 2π radian.	rad	rad/s (radian per detik), rad/s² (radian per detik kuadrat)	Putaran = radian / 2π Contoh: π radian = π / 2π = 0.5 putaran	Perhitungan sudut dalam GPS, representasi sudut dalam fungsi trigonometri

Kolom

Definisi

Simbol

Satuan Turunan

Rumus Konversi

Contoh Penggunaan

Definisi

Satu putaran penuh adalah satu putaran. Satu putaran penuh setara dengan 360 derajat.

put atau rev

RPM (putaran per menit), RPS (putaran per detik), Hz (Hertz, untuk frekuensi)

Radian = putaran

2π
Contoh

0.5 putaran = 0.5 – 2π = π radian

Kecepatan rotasi roda, kecepatan mesin

Definisi

Satu radian adalah sudut yang dibentuk ketika panjang busur lingkaran sama dengan panjang jari-jari lingkaran. Satu putaran penuh setara dengan 2π radian.

rad

rad/s (radian per detik), rad/s² (radian per detik kuadrat)

Putaran = radian / 2π
Contoh: π radian = π / 2π = 0.5 putaran

Perhitungan sudut dalam GPS, representasi sudut dalam fungsi trigonometri

Ilustrasi Visual

Berikut adalah ilustrasi visual yang membandingkan putaran dan radian:

Diagram Lingkaran yang Menunjukkan Satu Putaran Penuh:

Oke, mari kita mulai dengan mengubah putaran ke radian. Konsepnya mirip dengan memilih mangga harum manis yang tepat: kita perlu tahu ukurannya, warnanya, dan aromanya. Begitu pula dalam matematika, kita perlu memahami hubungan antara putaran dan radian. Nah, setelah menguasai konversi ini, Anda bisa melanjutkan dengan memilih buah favorit, dan untuk itu, Anda bisa membaca panduan lengkapnya di cara memilih mangga harum manis.

Kembali ke radian, transformasi ini krusial dalam berbagai bidang, mulai dari fisika hingga grafis komputer.

Sebuah lingkaran dibagi menjadi 360 bagian yang sama. Setiap bagian mewakili 1 derajat. Satu putaran penuh mengelilingi lingkaran, kembali ke titik awal, dan setara dengan 360 derajat.

Diagram Lingkaran yang Menunjukkan Nilai Radian:

Sebuah lingkaran dengan jari-jari r. Jika kita mengukur panjang busur yang sama dengan r, maka sudut yang dibentuk adalah 1 radian. Satu putaran penuh (360 derajat) setara dengan 2π radian.

Label yang Jelas pada Diagram:

Diagram lingkaran yang sama, dengan label yang menunjukkan hubungan antara derajat, radian, dan putaran. Tanda panah dan teks menunjukkan konversi dan ekuivalensi antara satuan-satuan tersebut.

Kuis Singkat

Berikut adalah kuis singkat untuk menguji pemahaman Anda tentang putaran dan radian:

Satuan yang digunakan untuk mengukur sudut berdasarkan rasio panjang busur terhadap jari-jari adalah:
1. Derajat
2. Putaran
3. Radian
4. Hertz
Satu putaran penuh setara dengan berapa radian?
1. π
2. 2π
3. 90
4. 360
Jika suatu roda berputar 2 putaran, berapa radian sudut yang ditempuh?
1. π
2. 2π
3. 3π
4. 4π
Satuan yang umum digunakan untuk mengukur kecepatan rotasi adalah:
1. rad/s
2. Hz
3. RPM
4. Semua benar
Dalam konteks fungsi trigonometri, satuan sudut yang paling sering digunakan adalah:
1. Derajat
2. Putaran
3. Radian
4. RPM

Contoh Kode Python

Berikut adalah contoh kode Python untuk mengkonversi antara putaran dan radian:

import math

def putaran_ke_radian(putaran):
    return putaran
- 2
- math.pi

def radian_ke_putaran(radian):
    return radian / (2
- math.pi)

# Contoh penggunaan
putaran = 0.5
radian = putaran_ke_radian(putaran)
print(f"putaran putaran = radian radian")

radian = math.pi
putaran = radian_ke_putaran(radian)
print(f"radian radian = putaran putaran")

Pilihlah putaran ketika berurusan dengan konsep rotasi yang intuitif dan mudah dipahami, seperti kecepatan putaran roda. Gunakan radian ketika bekerja dengan perhitungan matematika yang lebih kompleks, fungsi trigonometri, dan aplikasi yang memanfaatkan sifat geometris lingkaran, seperti dalam navigasi atau analisis gelombang.

Konversi Dasar

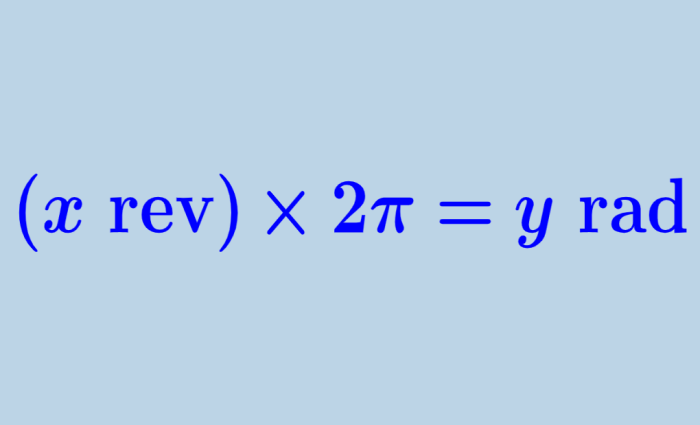
Source: identif.id

Selamat datang! Mari kita selami dunia konversi putaran ke radian. Konversi ini sangat krusial dalam berbagai bidang, mulai dari fisika hingga rekayasa, dan pemahaman yang kuat akan konsep ini membuka pintu ke pemahaman yang lebih dalam tentang gerakan melingkar. Artikel ini akan memandu Anda melalui langkah-langkah konversi, memberikan contoh konkret, dan menyajikan prosedur yang mudah diikuti.

Konversi Putaran ke Radian

Konversi putaran ke radian melibatkan penggunaan faktor konversi yang sederhana namun fundamental. Satu putaran penuh setara dengan 2π radian. Dengan memahami hubungan ini, kita dapat dengan mudah mengkonversi putaran ke radian menggunakan rumus berikut:

Radian = Putaran × 2π

Mari kita lihat contoh soal dan penyelesaiannya:

Contoh Soal: Konversikan 0.5 putaran ke radian.
Penyelesaian:

Identifikasi nilai putaran: 0.5
Gunakan rumus: Radian = 0.5 × 2π
Hitung: Radian = π ≈ 3.14159
Kesimpulan: 0.5 putaran setara dengan π radian (atau sekitar 3.14159 radian).

Prosedur Konversi Putaran ke Radian

Berikut adalah prosedur langkah-demi-langkah untuk mengonversi putaran ke radian:

Identifikasi Jumlah Putaran: Tentukan nilai putaran yang ingin Anda konversikan. Pastikan Anda memiliki nilai numerik yang jelas.
Gunakan Rumus Konversi: Kalikan jumlah putaran dengan 2π. Ini adalah langkah kunci dalam konversi.
Hitung Hasilnya: Lakukan perhitungan untuk mendapatkan nilai dalam radian. Jika perlu, gunakan kalkulator untuk presisi yang lebih tinggi.

Contoh Soal Cerita: Roda Berputar dan Jarum Jam

Mari kita terapkan konsep ini dalam beberapa contoh praktis:

Roda Berputar: Sebuah roda berputar sebanyak 3 putaran. Berapa radian sudut yang ditempuh roda tersebut?

Jumlah putaran: 3
Radian = 3 × 2π = 6π ≈ 18.84955 radian
Roda menempuh sudut sebesar 6π radian.

Jarum Jam: Jarum menit pada jam berputar satu kali dalam satu jam. Berapa radian sudut yang ditempuh jarum menit?

Satu putaran penuh jarum menit sama dengan 1 putaran.
Radian = 1 × 2π = 2π ≈ 6.28318 radian
Jarum menit menempuh sudut sebesar 2π radian.

Rumus dan Persamaan Penting

Dalam perjalanan kita mengonversi putaran ke radian, pemahaman mendalam tentang rumus dan persamaan yang mendasarinya sangat krusial. Ini bukan sekadar manipulasi angka, melainkan kunci untuk membuka pemahaman tentang hubungan geometris dan sudut dalam berbagai konteks. Mari kita selami lebih dalam untuk menguasai alat-alat penting ini.

Rumus Utama Konversi Putaran ke Radian

Rumus utama yang digunakan untuk mengonversi putaran ke radian adalah:

Radian = Putaran × 2π

Mari kita uraikan setiap variabel dalam rumus ini:

Radian: Ini adalah nilai sudut yang kita cari, dinyatakan dalam satuan radian.
Putaran: Ini adalah jumlah putaran yang ingin kita konversi. Satu putaran penuh setara dengan satu lingkaran penuh.
2π: Ini adalah konstanta matematika yang mewakili sudut dalam satu putaran penuh, setara dengan 360 derajat. Nilai π (pi) kira-kira sama dengan 3.14159.

Persamaan yang Menggambarkan Hubungan Putaran, Radian, dan Derajat

Hubungan antara putaran, radian, dan derajat dapat digambarkan melalui persamaan berikut:

Putaran ke Radian: Radian = Putaran × 2π
Radian ke Putaran: Putaran = Radian / 2π
Derajat ke Radian: Radian = Derajat × (π / 180)
Radian ke Derajat: Derajat = Radian × (180 / π)
Putaran ke Derajat: Derajat = Putaran × 360
Derajat ke Putaran: Putaran = Derajat / 360

Persamaan-persamaan ini memungkinkan kita untuk dengan mudah berpindah antara berbagai satuan sudut, memberikan fleksibilitas dalam menyelesaikan masalah yang melibatkan sudut.

Baiklah, mari kita bedah konversi putaran ke radian. Kita tahu, satu putaran penuh setara dengan 2π radian. Tapi, bagaimana kita mengaplikasikannya? Pemahaman ini sangat krusial, bahkan dalam konteks yang lebih luas seperti di bidang Pendidikan , di mana matematika menjadi fondasi berpikir logis. Mempelajari konversi ini melatih kita untuk berpikir analitis.

Kembali ke soal, mengubah putaran ke radian sesederhana mengalikan jumlah putaran dengan 2π. Mudah, bukan?

Contoh Penggunaan Rumus Konversi

Mari kita lihat beberapa contoh penggunaan rumus konversi dalam berbagai situasi:

Contoh 1: Mengonversi 0.5 putaran ke radian.

Menggunakan rumus: Radian = 0.5 × 2π ≈ 3.14 radian

Contoh 2: Mengonversi 1.25 putaran ke radian.

Menggunakan rumus: Radian = 1.25 × 2π ≈ 7.85 radian

Contoh 3: Mengonversi 90 derajat ke radian.

Menggunakan rumus: Radian = 90 × (π / 180) ≈ 1.57 radian

Contoh 4: Mengonversi 3π radian ke derajat.

Menggunakan rumus: Derajat = 3π × (180 / π) = 540 derajat

Contoh-contoh ini menunjukkan bagaimana rumus konversi dapat diterapkan dalam berbagai skenario, mulai dari perhitungan sederhana hingga masalah yang lebih kompleks.

Penggunaan Kalkulator Ilmiah untuk Konversi

Kalkulator ilmiah menyediakan cara mudah dan cepat untuk mengonversi putaran ke radian. Berikut adalah langkah-langkah umum:

Pastikan Mode Sudut yang Tepat: Periksa apakah kalkulator Anda diatur dalam mode radian. Jika tidak, ubah modenya.
Masukkan Nilai Putaran: Masukkan jumlah putaran yang ingin Anda konversi.
Kalikan dengan 2π: Gunakan tombol π (pi) pada kalkulator Anda dan kalikan nilai putaran dengan 2π.
Hasil: Hasil yang ditampilkan adalah nilai sudut dalam radian.

Sebagai contoh, jika Anda ingin mengonversi 0.75 putaran ke radian, Anda akan memasukkan 0.75 × 2π pada kalkulator, dan hasilnya akan mendekati 4.71 radian.

Aplikasi dalam Berbagai Bidang

Konversi putaran ke radian adalah keterampilan matematika fundamental yang melintasi berbagai disiplin ilmu dan rekayasa. Kemampuannya untuk menerjemahkan gerakan melingkar ke dalam satuan sudut yang konsisten dan mudah dikelola membuatnya sangat berharga dalam berbagai aplikasi. Mari kita telusuri bagaimana konversi ini diterapkan secara krusial dalam berbagai bidang, mulai dari perhitungan kecepatan sudut mesin hingga animasi komputer dan sistem navigasi canggih.

Pentingnya konversi putaran ke radian meluas jauh melampaui konsep matematika dasar. Dalam banyak bidang, konversi ini menjadi fondasi untuk analisis, desain, dan implementasi sistem yang kompleks. Tanpa kemampuan untuk secara akurat mengkonversi putaran ke radian, banyak teknologi modern yang kita andalkan saat ini tidak akan berfungsi sebagaimana mestinya.

Identifikasi Bidang Krusial

Konversi putaran ke radian memainkan peran penting dalam banyak bidang. Berikut adalah daftar lima bidang krusial yang sangat bergantung pada konversi ini, beserta penjelasan singkat tentang mengapa konversi ini sangat penting dan contoh spesifik dari sub-bidang atau aplikasi:

Teknik Mesin: Konversi ini penting untuk menganalisis dan mengontrol gerakan rotasi pada mesin. Contohnya adalah perhitungan kecepatan sudut poros engkol pada mesin pembakaran dalam.
Teknik Elektro: Konversi ini krusial dalam desain dan analisis motor listrik dan generator. Contohnya adalah perhitungan kecepatan rotasi rotor pada motor induksi.
Animasi Komputer: Konversi ini memungkinkan kontrol presisi terhadap rotasi objek dalam animasi. Contohnya adalah rotasi roda pada mobil animasi atau gerakan kepala karakter.
Navigasi: Konversi ini penting dalam sistem navigasi untuk menghitung posisi dan orientasi. Contohnya adalah penentuan posisi satelit GPS dan sistem navigasi pesawat terbang.
Robotika: Konversi ini digunakan untuk mengontrol gerakan sendi robot. Contohnya adalah perhitungan sudut rotasi pada lengan robot.

Aplikasi Teknik: Perhitungan Kecepatan Sudut

Dalam dunia teknik, pemahaman dan penerapan konversi putaran ke radian sangat penting untuk menghitung kecepatan sudut pada berbagai jenis mesin. Kecepatan sudut, yang diukur dalam radian per detik (rad/s), memberikan informasi tentang seberapa cepat suatu objek berputar. Mari kita lihat bagaimana konversi ini diterapkan secara rinci.

Untuk menghitung kecepatan sudut, kita seringkali memulai dengan informasi dalam putaran per menit (RPM). RPM mengukur berapa kali suatu objek berputar dalam satu menit. Untuk mengkonversi RPM ke rad/s, kita menggunakan langkah-langkah berikut:

Konversi RPM ke putaran per detik: Bagi RPM dengan 60 (detik dalam satu menit).
Konversi putaran ke radian: Kalikan jumlah putaran per detik dengan 2π (karena satu putaran penuh sama dengan 2π radian).

Contoh Perhitungan:

Misalkan sebuah poros mesin berputar pada 3000 RPM. Untuk menghitung kecepatan sudutnya dalam rad/s:

3000 RPM / 60 = 50 putaran per detik
50 putaran/detik

2π rad/putaran ≈ 314.16 rad/s

Jadi, kecepatan sudut poros mesin tersebut adalah sekitar 314.16 rad/s.

Ilustrasi Visual:

Bayangkan sebuah roda gigi yang terhubung ke poros mesin. Roda gigi ini berputar dengan kecepatan tertentu. Kecepatan sudut roda gigi ini penting untuk memahami kinerja mesin. Dengan mengetahui kecepatan sudut, kita dapat menghitung kecepatan linier dari titik-titik pada tepi roda gigi, yang penting untuk menggerakkan komponen lain dalam sistem.

Berbicara tentang perubahan, mengubah putaran ke radian memang membutuhkan sedikit perhitungan, mirip seperti saat kita perlu teliti membaca petunjuk. Sama halnya ketika Anda ingin tahu cara menggunakan test pack GP Care, Anda harus mengikuti langkah-langkahnya dengan cermat. Ketelitian adalah kunci, baik dalam menghitung sudut maupun dalam memahami hasil tes. Dengan begitu, kita bisa memastikan akurasi, entah itu dalam matematika atau dalam hal kesehatan.

Studi Kasus:

Kesalahan dalam konversi putaran ke radian dapat berdampak signifikan pada kinerja mesin. Misalkan, dalam sistem kontrol mesin, kesalahan konversi menyebabkan perhitungan kecepatan sudut yang salah. Hal ini dapat menyebabkan:

Kinerja yang tidak efisien: Mesin mungkin beroperasi pada kecepatan yang tidak optimal, yang mengurangi efisiensi bahan bakar atau konsumsi energi.
Kerusakan komponen: Kecepatan yang tidak tepat dapat menyebabkan keausan dini pada komponen mesin, bahkan kerusakan yang parah.
Kegagalan sistem: Dalam sistem yang lebih kompleks, kesalahan konversi dapat menyebabkan kegagalan sistem secara keseluruhan.

Animasi Komputer: Kontrol Gerakan Objek

Dalam animasi komputer, konversi putaran ke radian adalah kunci untuk mengontrol gerakan objek secara presisi dan realistis. Hal ini memungkinkan animator untuk menentukan rotasi, pergerakan berbasis fisika, dan gerakan karakter dengan akurasi yang tinggi.

Kontrol Rotasi Objek:

Konversi putaran ke radian memungkinkan animator untuk mengontrol rotasi objek. Misalnya, dalam animasi roda yang berputar, konversi ini digunakan untuk menentukan berapa banyak radian roda harus berputar setiap frame untuk mencapai kecepatan yang diinginkan. Dalam animasi kepala karakter yang menoleh, konversi ini digunakan untuk menentukan sudut rotasi kepala dalam radian.

Pergerakan Berbasis Fisika:

Dalam simulasi fisika, seperti simulasi bola yang memantul, konversi putaran ke radian digunakan untuk menghitung sudut pantulan bola berdasarkan kecepatan dan sudut datang. Hal ini memungkinkan animasi yang realistis.

Animasi Karakter:

Dalam animasi karakter, konversi putaran ke radian digunakan untuk mengontrol gerakan sendi karakter. Misalnya, untuk menggerakkan lengan karakter, animator menggunakan konversi ini untuk menentukan sudut rotasi pada sendi bahu, siku, dan pergelangan tangan.

Contoh Kode (Python):

Berikut adalah contoh kode Python sederhana yang menunjukkan bagaimana konversi putaran ke radian dapat digunakan untuk mengontrol rotasi objek:

import math

def putaran_ke_radian(putaran):
    return putaran
- 2
- math.pi

# Contoh penggunaan
putaran = 1
radian = putaran_ke_radian(putaran)
print(f"putaran putaran = radian radian") # Output: 1 putaran = 6.283185307179586 radian

# Mengontrol rotasi objek dalam animasi (contoh sederhana)
kecepatan_rotasi_rpm = 60  # Contoh: 60 RPM
kecepatan_rotasi_rps = kecepatan_rotasi_rpm / 60  # Putaran per detik
kecepatan_rotasi_radian = kecepatan_rotasi_rps
- 2
- math.pi

print(f"Kecepatan rotasi dalam radian per detik: kecepatan_rotasi_radian")

Tantangan Umum:

Beberapa tantangan umum dalam menggunakan konversi putaran ke radian dalam animasi meliputi:

Sinkronisasi: Memastikan bahwa rotasi objek disinkronkan dengan elemen animasi lainnya.
Interpolasi: Menghaluskan gerakan objek dengan menginterpolasi nilai radian dari satu frame ke frame berikutnya.
Perhitungan Fisika: Mengintegrasikan konversi putaran ke radian dengan perhitungan fisika untuk menghasilkan gerakan yang realistis.

Navigasi: Pentingnya Konversi

Konversi putaran ke radian sangat penting dalam sistem navigasi, di mana akurasi posisi dan orientasi adalah kunci. Konversi ini digunakan dalam berbagai aplikasi navigasi, mulai dari penentuan posisi satelit hingga navigasi pesawat terbang dan kapal.

Penentuan Posisi Satelit (GPS):

Sistem GPS menggunakan satelit yang mengorbit Bumi untuk menentukan posisi pengguna. Konversi putaran ke radian digunakan dalam perhitungan untuk menentukan sudut elevasi dan azimut satelit, yang diperlukan untuk menghitung jarak ke satelit dan akhirnya posisi pengguna.

Sistem Navigasi Inersia (INS):

Sistem INS menggunakan sensor seperti giroskop dan akselerometer untuk melacak posisi dan orientasi. Konversi putaran ke radian digunakan untuk mengintegrasikan data dari sensor giroskop untuk menghitung perubahan sudut dan orientasi. Informasi ini kemudian digunakan untuk menentukan posisi dan arah.

Navigasi Pesawat Terbang dan Kapal:

Dalam navigasi pesawat terbang dan kapal, konversi putaran ke radian digunakan untuk menghitung sudut belok, heading, dan jarak tempuh. Ini memungkinkan sistem navigasi untuk mengarahkan pesawat atau kapal ke tujuan dengan presisi.

Contoh Kasus:

Misalkan sebuah pesawat terbang mengubah arah sebesar 10 derajat. Untuk menghitung perubahan posisi pesawat, kita perlu mengkonversi sudut ini ke radian:

10 derajat – (π / 180) ≈ 0.1745 radian

Dengan mengetahui perubahan sudut dalam radian, sistem navigasi dapat menghitung perubahan posisi pesawat berdasarkan jarak tempuh dan arah. Semakin akurat konversi, semakin tepat perhitungan posisi pesawat.

Dampak Kesalahan Konversi:

Kesalahan dalam konversi putaran ke radian dapat memiliki konsekuensi serius dalam navigasi:

Kesalahan Posisi: Kesalahan kecil dalam konversi dapat menyebabkan kesalahan signifikan dalam perhitungan posisi, yang dapat menyebabkan pesawat atau kapal keluar dari jalur yang benar.
Kesalahan Arah: Kesalahan konversi dapat menyebabkan kesalahan dalam penentuan arah, yang dapat membahayakan navigasi.
Keselamatan: Dalam kasus ekstrem, kesalahan navigasi dapat menyebabkan kecelakaan atau insiden keselamatan lainnya.

Tambahan: Bidang Aplikasi Alternatif

Selain bidang yang telah disebutkan, konversi putaran ke radian juga diterapkan dalam beberapa bidang aplikasi alternatif. Meskipun mungkin tidak seumum bidang-bidang sebelumnya, peran konversi ini tetap penting.

Robotika: Dalam robotika, konversi putaran ke radian digunakan untuk mengontrol gerakan sendi robot.
Pemrosesan Sinyal: Dalam pemrosesan sinyal, konversi putaran ke radian digunakan dalam analisis frekuensi dan representasi sinyal.
Analisis Data: Dalam analisis data, konversi putaran ke radian digunakan untuk mengolah data yang melibatkan gerakan melingkar.

Contoh Soal dan Latihan

Untuk memperdalam pemahaman tentang konversi putaran ke radian, mari kita bedah beberapa contoh soal dan latihan. Soal-soal ini dirancang dengan tingkat kesulitan yang bervariasi, mulai dari yang sederhana hingga yang lebih kompleks, untuk menguji kemampuan Anda dalam mengaplikasikan konsep yang telah dipelajari. Selain itu, kami akan menyediakan kunci jawaban untuk setiap soal, serta kuis singkat untuk menguji pemahaman Anda secara cepat.

Soal Latihan Konversi Putaran ke Radian

Berikut adalah beberapa soal latihan yang dapat Anda gunakan untuk menguji pemahaman Anda tentang konversi putaran ke radian. Soal-soal ini mencakup berbagai tingkat kesulitan, mulai dari konversi dasar hingga soal yang melibatkan konsep matematika lainnya.

Soal 1: Konversikan 2 putaran ke radian.
Soal 2: Konversikan 0.5 putaran ke radian.
Soal 3: Sebuah roda berputar sebanyak 3.75 putaran. Berapa radiankah sudut yang ditempuh roda tersebut?
Soal 4: Sebuah lingkaran memiliki jari-jari 10 cm. Jika sebuah busur lingkaran memiliki panjang 15 cm, berapa putaran sudut pusat yang bersesuaian dengan busur tersebut?
Soal 5: Sebuah roda berputar dengan kecepatan 120 putaran per menit. Berapa radian per detik kecepatan sudut roda tersebut?

Kunci Jawaban

Berikut adalah kunci jawaban untuk soal-soal latihan di atas:

Jawaban 1: 2 putaran = 2

2π radian = 4π radian ≈ 12.57 radian
Jawaban 2: 0.5 putaran = 0.5

2π radian = π radian ≈ 3.14 radian
Jawaban 3: 3.75 putaran = 3.75

2π radian = 7.5π radian ≈ 23.56 radian
Jawaban 4: Panjang busur (s) = r

θ, dimana θ dalam radian.

15 cm = 10 cm – θ
θ = 1.5 radian. Untuk mencari putaran, θ (dalam radian) dibagi dengan 2π.
1. 5 radian / 2π ≈ 0.24 putaran.
Jawaban 5: 120 putaran per menit = (120
2π) radian per menit = 240π radian per menit. Untuk mengubah ke radian per detik, bagi dengan 60

(240π / 60) radian per detik = 4π radian per detik ≈ 12.57 radian per detik.

Soal Latihan yang Lebih Kompleks

Berikut adalah soal-soal yang menggabungkan konversi putaran ke radian dengan konsep matematika lainnya, seperti trigonometri:

Soal 1: Sebuah benda bergerak melingkar dengan jari-jari 5 cm. Jika benda tersebut telah menempuh sudut sebesar 3π/4 radian, berapakah panjang lintasan yang ditempuh benda tersebut?
Soal 2: Sebuah roda dengan diameter 1 meter berputar sebanyak 10 putaran. Berapakah jarak yang ditempuh oleh suatu titik pada tepi roda tersebut?
Soal 3: Sebuah segitiga siku-siku memiliki sudut pusat sebesar π/3 radian pada lingkaran dengan jari-jari 8 cm. Hitunglah luas juring lingkaran yang dibentuk oleh sudut tersebut.

Kunci Jawaban Soal Kompleks

Berikut adalah kunci jawaban untuk soal-soal kompleks:

Jawaban 1: Panjang lintasan (s) = r – θ.
s = 5 cm – (3π/4) ≈ 11.78 cm
Jawaban 2: Jarak yang ditempuh = jumlah putaran

keliling roda.

Keliling roda = π
- diameter = π
- 1 m = π m.
Jarak = 10

π m ≈ 31.42 m
Jawaban 3: Luas juring = (1/2)
- r ²
- θ.
Luas juring = (1/2)
- (8 cm) ²
- (π/3) ≈ 33.51 cm ²

Kuis Singkat: Pilihan Ganda

Berikut adalah kuis singkat untuk menguji pemahaman Anda tentang konversi putaran ke radian. Pilihlah jawaban yang paling tepat:

Soal 1: Berapa radiankah 1/4 putaran?
1. π/4
2. π/2
3. π
4. 2π
Soal 2: Jika sebuah roda berputar 180 derajat, berapa radiankah sudut yang ditempuh?
1. π/4
2. π/2
3. π
4. 2π
Soal 3: Konversikan 3 putaran ke radian.
1. π
2. 2π
3. 3π
4. 6π
Soal 4: Berapa putaran yang setara dengan 3π radian?
1. 0.5
2. 1
3. 1.5
4. 3
Soal 5: Sebuah benda berputar sebanyak 720 derajat. Berapa radiankah sudut yang ditempuh?
1. π
2. 2π
3. 3π
4. 4π

Kunci Jawaban Kuis

Berikut adalah kunci jawaban untuk kuis pilihan ganda:

Jawaban: b. π/2
Jawaban: c. π
Jawaban: d. 6π
Jawaban: c. 1.5
Jawaban: d. 4π

Visualisasi Konversi: Cara Mengubah Putaran Ke Radian

Memahami konversi putaran ke radian menjadi lebih mudah dengan bantuan visualisasi. Ilustrasi interaktif, diagram, dan animasi menawarkan cara yang intuitif untuk memahami hubungan antara putaran dan radian. Melalui visualisasi ini, konsep yang mungkin terasa abstrak dapat diakses dan dipahami dengan lebih baik.

Oke, mari kita mulai dengan konversi putaran ke radian. Ini krusial dalam banyak perhitungan, termasuk dalam bidang teknik sipil. Tapi, tahukah Anda bahwa pemahaman tentang sudut juga penting ketika kita berbicara tentang biaya? Misalnya, dalam proyek pengukuran tanah, akurasi sudut sangat memengaruhi perhitungan luas dan akhirnya, cara menghitung biaya pengukuran tanah. Kembali ke radian, konversi yang tepat memastikan kita mendapatkan hasil yang presisi, yang pada gilirannya, berdampak pada efisiensi biaya dan keberhasilan proyek secara keseluruhan.

Ilustrasi Interaktif Konversi

Ilustrasi interaktif memungkinkan pengguna untuk memasukkan nilai putaran dan langsung melihat konversinya ke radian. Fitur ini sangat bermanfaat karena:

Pengguna dapat bereksperimen dengan berbagai nilai putaran.
Visualisasi memberikan umpan balik instan, memungkinkan pemahaman yang cepat.
Ilustrasi interaktif dapat mencakup tampilan grafik lingkaran yang dinamis, menunjukkan bagaimana nilai putaran berkorespondensi dengan sudut dalam radian.

Diagram Lingkaran untuk Konversi

Diagram lingkaran adalah alat visual yang sangat efektif untuk menunjukkan konversi putaran ke radian. Diagram ini biasanya menampilkan:

Lingkaran penuh yang mewakili satu putaran (360 derajat atau 2π radian).
Garis-garis radial yang membagi lingkaran menjadi segmen-segmen, yang masing-masing mewakili sudut tertentu dalam radian. Misalnya, π/2 radian (90 derajat), π radian (180 derajat), dan 3π/2 radian (270 derajat).
Penjelasan visual tentang bagaimana sudut dalam putaran berkorespondensi dengan panjang busur pada lingkaran.

Relasi Putaran dan Radian pada Grafik Fungsi Trigonometri

Grafik fungsi trigonometri, seperti sinus dan kosinus, memberikan cara yang sangat baik untuk memvisualisasikan hubungan antara putaran dan radian. Dengan memplot fungsi terhadap sumbu yang berlabel dalam radian, pengguna dapat melihat:

Bagaimana nilai fungsi berubah seiring dengan perubahan sudut dalam radian.
Pola periodik dari fungsi trigonometri, yang berulang setiap 2π radian (satu putaran).
Titik-titik penting pada grafik, seperti titik nol, titik maksimum, dan titik minimum, yang sesuai dengan sudut-sudut tertentu dalam radian.

Animasi Roda Berputar

Animasi sederhana yang menunjukkan roda berputar adalah cara yang efektif untuk mengilustrasikan konversi putaran ke radian dalam konteks dunia nyata. Animasi ini dapat menampilkan:

Sebuah roda yang berputar, dengan penanda pada tepi roda untuk menunjukkan posisi awal.
Penghitung yang melacak jumlah putaran roda.
Tampilan sudut dalam radian yang sesuai dengan putaran roda.
Garis yang menunjukkan panjang busur yang telah ditempuh oleh titik pada tepi roda, yang berkorespondensi dengan sudut dalam radian.

Perbedaan dengan Satuan Sudut Lainnya

Memahami perbedaan antara radian, derajat, dan gradian sangat penting untuk menguasai konsep sudut dan penerapannya dalam berbagai bidang. Setiap satuan memiliki karakteristik unik dalam hal definisi, penggunaan, dan konversi. Perbandingan ini akan membantu kita memahami keunggulan dan kekurangan masing-masing satuan, serta bagaimana mereka digunakan dalam konteks matematika, sains, dan rekayasa.

Mari kita telusuri perbedaan mendasar dan bagaimana satuan-satuan ini berinteraksi.

Perbandingan Konversi:

Proses konversi dari putaran penuh (satu revolusi) ke satuan radian, derajat, dan gradian melibatkan prinsip matematika yang berbeda. Perbedaan ini terletak pada cara sudut diukur dan dinyatakan.

Radian: Radian mengukur sudut berdasarkan panjang busur lingkaran yang dibentuk oleh sudut tersebut. Satu putaran penuh setara dengan 2π radian. Konversi ke radian didasarkan pada hubungan langsung antara sudut pusat dan panjang busur.
Derajat: Derajat membagi lingkaran menjadi 360 bagian yang sama. Satu putaran penuh setara dengan 360 derajat. Konversi ke derajat didasarkan pada pembagian lingkaran menjadi bagian-bagian yang sama.
Gradian: Gradian membagi lingkaran menjadi 400 bagian yang sama. Satu putaran penuh setara dengan 400 gradian. Konversi ke gradian juga didasarkan pada pembagian lingkaran, tetapi dengan jumlah bagian yang berbeda.

Perbedaan presisi dalam perhitungan sudut bergantung pada kebutuhan aplikasi. Radian seringkali memberikan presisi tertinggi dalam kalkulus dan trigonometri karena hubungannya yang alami dengan fungsi trigonometri. Derajat dan gradian lebih umum digunakan dalam aplikasi praktis di mana presisi tinggi mungkin tidak selalu diperlukan.

Tabel Perbandingan:

Berikut adalah tabel yang membandingkan ketiga satuan sudut, memberikan definisi, simbol, faktor konversi, contoh penggunaan, kelebihan, dan kekurangan masing-masing.

Satuan	Definisi	Simbol	Faktor Konversi ke Putaran Penuh	Contoh Penggunaan	Kelebihan	Kekurangan
Radian	Sudut yang dibentuk oleh busur lingkaran yang panjangnya sama dengan jari-jari lingkaran.	rad	2π rad = 1 putaran	Matematika: Kalkulus, trigonometri. Fisika: Rotasi, osilasi. Grafik Komputer: Representasi sudut dalam transformasi.	Alami dalam kalkulus dan analisis matematika. Memudahkan perhitungan dengan fungsi trigonometri. Satuan SI untuk sudut.	Kurang intuitif bagi sebagian orang. Tidak umum digunakan dalam aplikasi sehari-hari.
Derajat	Sudut yang membagi lingkaran menjadi 360 bagian yang sama.	°	360° = 1 putaran	Navigasi: Penentuan arah kompas. Teknik: Pengukuran sudut dalam konstruksi. Geometri: Pengukuran sudut dalam bangun datar.	Intuitif dan mudah dipahami. Banyak digunakan dalam aplikasi sehari-hari.	Kurang alami dalam kalkulus. Membutuhkan konversi untuk beberapa perhitungan matematika.
Gradian	Sudut yang membagi lingkaran menjadi 400 bagian yang sama.	grad atau g	400 grad = 1 putaran	Surveying (terutama di Eropa). Beberapa aplikasi teknik.	Memudahkan perhitungan dalam sistem desimal. Relatif mudah dikonversi ke derajat.	Tidak umum digunakan di luar bidang tertentu. Kurang intuitif dibandingkan derajat.

Sebagai contoh visualisasi, bayangkan lingkaran dibagi menjadi beberapa bagian. Untuk radian, kita melihat hubungan antara sudut pusat dan panjang busur. Untuk derajat, lingkaran dibagi menjadi 360 bagian yang sama. Untuk gradian, lingkaran dibagi menjadi 400 bagian yang sama.

Analisis Kelebihan dan Kekurangan:

Setiap satuan sudut memiliki kelebihan dan kekurangan yang membuatnya lebih cocok untuk aplikasi tertentu.

Matematika Teoretis: Radian adalah pilihan utama dalam kalkulus dan trigonometri karena menyederhanakan perhitungan dan memberikan hubungan alami dengan fungsi trigonometri. Derajat dan gradian kurang ideal dalam konteks ini karena memerlukan faktor konversi tambahan.
Aplikasi Praktis: Derajat adalah satuan yang paling umum digunakan dalam pengukuran sudut di lapangan, desain teknik, dan animasi karena kemudahan penggunaannya dan intuitif. Gradian digunakan dalam beberapa aplikasi survei dan teknik, terutama di Eropa.
Kemudahan Penggunaan: Derajat lebih mudah digunakan dalam kalkulasi manual dan penggunaan kalkulator atau perangkat lunak. Radian memerlukan pemahaman tentang nilai π, sementara gradian kurang dikenal secara umum.
Standarisasi Internasional: Radian adalah satuan sudut yang diakui dalam Sistem Internasional (SI), menjadikannya standar untuk pengukuran sudut dalam sains dan teknik di seluruh dunia.

Konversi Antar Satuan:

Konversi antara derajat, gradian, dan radian melibatkan penggunaan rumus matematika sederhana. Berikut adalah langkah-langkah dan contoh untuk setiap pasangan konversi.

Derajat ke Radian:
Gunakan rumus: radian = derajat × (π / 180)

Contoh: Konversikan 45 derajat ke radian. radian = 45 × (π / 180) = π / 4 ≈ 0.785 rad
Radian ke Derajat:
Gunakan rumus: derajat = radian × (180 / π)

Contoh: Konversikan π/2 radian ke derajat. derajat = (π/2) × (180 / π) = 90°
Gradian ke Derajat:
Gunakan rumus: derajat = gradian × (90 / 100)

Contoh: Konversikan 200 gradian ke derajat. derajat = 200 × (90 / 100) = 180°
Derajat ke Gradian:
Gunakan rumus: gradian = derajat × (100 / 90)

Contoh: Konversikan 90 derajat ke gradian. gradian = 90 × (100 / 90) = 100 grad
Radian ke Gradian:
Gunakan rumus: gradian = radian × (200 / π)

Contoh: Konversikan π/2 radian ke gradian. gradian = (π/2) × (200 / π) = 100 grad
Gradian ke Radian:
Gunakan rumus: radian = gradian × (π / 200)

Contoh: Konversikan 100 gradian ke radian. radian = 100 × (π / 200) = π / 2 ≈ 1.57 rad

Contoh kode dalam Python untuk konversi:

import math

def derajat_ke_radian(derajat):
    return derajat
- (math.pi / 180)

def radian_ke_derajat(radian):
    return radian
- (180 / math.pi)

def gradian_ke_derajat(gradian):
    return gradian
- (90 / 100)

def derajat_ke_gradian(derajat):
    return derajat
- (100 / 90)

# Contoh penggunaan
derajat = 45
radian = derajat_ke_radian(derajat)
print(f"derajat derajat = radian radian")

radian = math.pi/2
derajat = radian_ke_derajat(radian)
print(f"radian radian = derajat derajat")

Dalam konteks proyeksi peta, konversi antara berbagai sistem koordinat geografis (misalnya, dari lintang/bujur dalam derajat ke koordinat proyeksi dalam meter) sering melibatkan konversi dari derajat ke radian untuk perhitungan trigonometri yang akurat.

Tambahan (Opsional):

Sebagai tambahan, berikut adalah beberapa aspek terkait yang bisa memperkaya pemahaman tentang satuan sudut.

Sejarah Singkat: Derajat telah digunakan sejak zaman Babilonia kuno, dengan pembagian lingkaran menjadi 360 bagian. Radian muncul kemudian, seiring dengan perkembangan kalkulus dan trigonometri. Gradian relatif lebih modern dan dikembangkan untuk mempermudah perhitungan desimal.
Aplikasi Lanjutan: Dalam astronomi, sudut digunakan untuk mengukur posisi bintang dan planet. Dalam fisika, sudut sangat penting dalam analisis gerakan rotasi dan osilasi. Robotika menggunakan sudut untuk mengontrol gerakan sendi robot.
Standar Internasional: Radian adalah satuan sudut yang diakui dalam Sistem Internasional (SI), yang menekankan pentingnya dalam sains dan rekayasa modern.

Kesalahan Umum dan Cara Mengatasinya (Konversi Putaran ke Radian)

Konversi putaran ke radian adalah keterampilan penting dalam matematika dan fisika. Namun, proses ini seringkali menjadi sumber kesalahan bagi banyak orang. Memahami kesalahan umum dan cara mengatasinya akan sangat membantu dalam meningkatkan akurasi perhitungan dan pemahaman konsep.

Mari kita selami kesalahan-kesalahan yang sering terjadi dan bagaimana cara menghindarinya.

Identifikasi Kesalahan Umum

Konversi putaran ke radian melibatkan beberapa langkah yang rentan terhadap kesalahan. Kesalahan-kesalahan ini dapat dikategorikan menjadi beberapa jenis utama, yang meliputi kesalahan konseptual, kesalahan perhitungan, dan kesalahan penggunaan unit. Mari kita lihat lebih detail:

Kesalahan Konseptual: Kesalahan ini muncul akibat kurangnya pemahaman tentang konsep dasar lingkaran dan sudut.

Contoh: Menganggap 1 putaran sama dengan 1 radian, atau kebingungan antara derajat dan radian.
Penyebab: Kurangnya pemahaman tentang definisi radian sebagai rasio panjang busur terhadap jari-jari lingkaran.

Kesalahan Perhitungan: Kesalahan ini terjadi saat melakukan perhitungan matematika yang diperlukan untuk konversi.

Contoh: Salah mengalikan atau membagi dengan faktor konversi (2π atau π).
Penyebab: Kurang teliti dalam melakukan perhitungan atau kesalahan dalam menggunakan kalkulator.

Kesalahan Penggunaan Unit: Kesalahan ini muncul akibat ketidakjelasan tentang unit yang digunakan dalam perhitungan.

Contoh: Menggunakan derajat dalam perhitungan yang seharusnya menggunakan radian, atau sebaliknya.
Penyebab: Kurangnya perhatian terhadap unit yang digunakan dalam soal atau perhitungan.

Tips untuk Menghindari Kesalahan

Untuk menghindari kesalahan dalam konversi putaran ke radian, beberapa tips praktis dapat diterapkan. Tips ini mencakup pemahaman konsep, penggunaan alat bantu yang tepat, dan pengecekan hasil.

Pahami Konsep Dasar: Pastikan Anda memahami definisi radian dan hubungan antara putaran, derajat, dan radian. Visualisasikan lingkaran dan sudut-sudutnya.

Tips: Gunakan diagram lingkaran untuk memvisualisasikan konversi. Misalnya, gambarlah lingkaran dan bagi menjadi beberapa bagian untuk merepresentasikan sudut dalam radian. Ingat bahwa satu putaran penuh adalah 2π radian.

Gunakan Faktor Konversi yang Tepat: Selalu gunakan faktor konversi yang benar (2π radian per putaran).

Tips: Hafalkan faktor konversi atau tuliskan di catatan Anda.

Perhatikan Unit: Selalu perhatikan unit yang digunakan dalam perhitungan. Pastikan semua unit konsisten sebelum melakukan perhitungan.

Tips: Tuliskan unit di setiap langkah perhitungan untuk menghindari kesalahan.

Gunakan Alat Bantu dengan Hati-hati: Gunakan kalkulator atau konverter online, tetapi selalu periksa hasilnya.

Tips: Verifikasi hasil menggunakan perhitungan manual atau perbandingan dengan nilai-nilai yang diketahui.

Uji Pemahaman Konsep Dasar: Sebelum melakukan perhitungan konversi, ujilah pemahaman Anda tentang konsep dasar.

Tips: Kerjakan soal-soal latihan sederhana untuk menguji pemahaman Anda.

Memeriksa Keakuratan Hasil Konversi

Memeriksa keakuratan hasil konversi adalah langkah penting untuk memastikan tidak ada kesalahan. Ada beberapa metode yang dapat digunakan untuk melakukan pengecekan ini.

Perhitungan Manual: Lakukan perhitungan konversi secara manual untuk memverifikasi hasil.

Tips: Gunakan rumus konversi: radian = putaran × 2π.

Penggunaan Rumus: Gunakan rumus konversi yang benar untuk memverifikasi hasil.

Tips: Pastikan Anda menggunakan rumus yang tepat untuk konversi yang Anda lakukan.

Perbandingan dengan Nilai yang Diketahui: Bandingkan hasil konversi dengan nilai-nilai yang diketahui.

Contoh: Ketahui bahwa 1 putaran = 2π radian.

Penggunaan Kalkulator Ilmiah: Gunakan kalkulator ilmiah untuk memverifikasi hasil.

Tips: Pastikan kalkulator Anda diatur ke mode radian jika Anda melakukan perhitungan dengan radian.

Mengidentifikasi dan Memperbaiki Kesalahan: Jika hasil konversi tidak akurat, identifikasi kesalahan dan perbaiki.

Tips: Periksa kembali setiap langkah perhitungan dan pastikan tidak ada kesalahan.

Contoh Kasus dan Solusi

Mari kita lihat beberapa contoh kasus nyata yang menunjukkan kesalahan umum dalam konversi putaran ke radian, beserta solusinya:

Contoh Kasus 1: Seorang siswa ingin mengkonversi 0.5 putaran ke radian. Siswa tersebut salah mengalikan 0.5 dengan π alih-alih 2π.

Kesalahan yang Terjadi: Menggunakan faktor konversi yang salah (π) alih-alih (2π).

Langkah yang Salah: 0. 5 putaran × π = 1.57 radian

Solusi:

Langkah 1: Gunakan rumus yang benar: radian = putaran × 2π
Langkah 2: Masukkan nilai: radian = 0.5 × 2π
Langkah 3: Hitung: radian = π ≈ 3.14 radian

Hasil Akhir: 3.14 radian

Contoh Kasus 2: Seorang insinyur ingin menghitung sudut rotasi roda yang berputar 1.75 putaran. Ia salah dalam melakukan perhitungan, yaitu mengalikan 1.75 dengan 2, bukannya 2π.

Kesalahan yang Terjadi: Kesalahan dalam mengalikan dengan faktor konversi yang salah.

Langkah yang Salah: 1.75 putaran × 2 = 3.5 radian

Solusi:

Langkah 1: Gunakan rumus: radian = putaran × 2π
Langkah 2: Masukkan nilai: radian = 1.75 × 2π
Langkah 3: Hitung: radian = 3.5π ≈ 10.99 radian

Hasil Akhir: 10.99 radian

Contoh Kasus 3: Seorang siswa kebingungan antara derajat dan radian, dan mencoba mengkonversi putaran ke derajat, lalu ke radian.

Kesalahan yang Terjadi: Kebingungan antara unit dan melakukan konversi yang tidak perlu.

Memahami konversi putaran ke radian memang krusial, misalnya satu putaran penuh setara dengan 2π radian. Tapi, pernahkah Anda berpikir bagaimana konsep ini diterapkan dalam dunia nyata? Mari kita sejenak beralih, bayangkan bagaimana Identif , sebagai contoh, mungkin memanfaatkan prinsip-prinsip ini dalam analisis data mereka. Kembali ke matematika, mengubah putaran ke radian pada dasarnya adalah mengalikan jumlah putaran dengan 2π.

Mudah, bukan?

Langkah yang Salah: 1 putaran = 360 derajat; 360 derajat × π/180 = 6.28 radian (padahal seharusnya langsung 1 putaran = 2π)

Solusi:

Langkah 1: Pahami bahwa 1 putaran = 2π radian.
Langkah 2: Jika perlu, gunakan rumus: radian = putaran × 2π
Langkah 3: Untuk 1 putaran, radian = 1 × 2π = 2π ≈ 6.28 radian

Hasil Akhir: 6.28 radian

Alat Bantu Konversi

Source: kompas.com

Dalam matematika dan sains, konversi antara putaran dan radian adalah keterampilan fundamental. Kemampuan untuk dengan cepat dan akurat mengubah satuan sudut ini sangat penting dalam berbagai aplikasi, mulai dari rekayasa dan fisika hingga grafis komputer dan animasi. Untungnya, ada banyak alat dan sumber daya yang tersedia untuk membantu mempermudah proses konversi ini.

Mari kita telaah berbagai alat bantu konversi yang tersedia, mulai dari kalkulator online hingga aplikasi kalkulator, serta merancang kalkulator sederhana sendiri. Dengan memahami pilihan yang ada, pengguna dapat memilih alat yang paling sesuai dengan kebutuhan mereka dan memastikan akurasi dalam perhitungan mereka.

Identifikasi Alat Bantu Konversi Online

Berikut adalah lima alat bantu konversi online yang sangat baik untuk mengonversi putaran (revolutions) ke radian:

Calculator.net: Menyediakan konverter sudut yang komprehensif. Calculator.net Angle Converter
RapidTables: Menawarkan konverter satuan yang mudah digunakan. RapidTables Revolution to Radian Converter
Unit Converter: Alat konversi serbaguna untuk berbagai satuan. Unit Converter Revolutions to Radians
Convert.net: Konverter satuan online yang sederhana dan efisien. Convert.net Revolutions to Radians
Math is Fun: Menyediakan konverter sudut interaktif. Math is Fun Radians/Degrees Converter (Meskipun tidak secara khusus menyebut “revolutions,” konversi ke derajat, yang kemudian dapat diubah ke radian, dapat dilakukan).

Panduan Penggunaan Alat Bantu Konversi Online

Berikut adalah panduan langkah demi langkah untuk menggunakan beberapa alat bantu konversi online yang disebutkan di atas:

Calculator.net

Kunjungi situs web Calculator.net dan navigasikan ke halaman konversi sudut.
Pilih “Revolutions” sebagai satuan input.
Masukkan nilai putaran yang ingin Anda konversi ke dalam kotak input yang sesuai.
Pilih “Radians” sebagai satuan output.
Klik tombol “Convert” atau tombol serupa untuk mendapatkan hasilnya.
Hasil konversi akan ditampilkan di kotak output.

RapidTables

Kunjungi halaman RapidTables untuk konversi putaran ke radian.
Masukkan nilai putaran dalam kotak input yang berlabel “Revolutions”.
Hasil konversi ke radian akan langsung ditampilkan di kotak output yang berlabel “Radians”.

Unit Converter

Buka halaman Unit Converter untuk konversi putaran ke radian.
Masukkan nilai putaran di kotak input.
Pilih “Revolutions” sebagai satuan input dan “Radians” sebagai satuan output jika diperlukan (biasanya sudah terpilih secara default).
Hasil konversi akan secara otomatis ditampilkan.

Convert.net

Akses halaman Convert.net untuk konversi putaran ke radian.
Masukkan nilai putaran dalam kotak input.
Pilih “Revolutions” sebagai satuan input dan “Radians” sebagai satuan output.
Hasil konversi akan segera ditampilkan.

Math is Fun (Menggunakan Konversi ke Derajat)

Kunjungi halaman Math is Fun untuk konversi derajat ke radian.
Gunakan konverter untuk mengkonversi putaran ke derajat (1 putaran = 360 derajat).
Masukkan nilai derajat yang diperoleh ke dalam konverter radian.
Hasilnya akan menampilkan nilai dalam radian.

Catatan: Tangkapan layar untuk setiap alat bantu konversi akan menunjukkan antarmuka pengguna yang spesifik dan langkah-langkah yang dijelaskan di atas. Karena keterbatasan format, ilustrasi visual tidak dapat disertakan, tetapi panduan di atas memberikan deskripsi yang jelas tentang cara menggunakan setiap alat.

Aplikasi Kalkulator dengan Fungsi Konversi

Berikut adalah daftar tiga aplikasi kalkulator yang mendukung konversi putaran ke radian:

Kalkulator di iOS (iPhone/iPad):
- Platform: iOS
- Akses: Aplikasi Kalkulator bawaan pada perangkat iOS.
- Cara Menggunakan:
  1. Buka aplikasi Kalkulator.
  2. Putar perangkat Anda ke mode lanskap untuk mengakses fungsi kalkulator ilmiah.
  3. Masukkan nilai putaran (setelah mengkonversinya ke derajat, yaitu putaran
    – 360).
  4. Tekan tombol “deg” (derajat) untuk mengubah input menjadi derajat.
  5. Tekan tombol “rad” (radian) untuk mengkonversi derajat ke radian.
  6. Hasil konversi akan ditampilkan.
Kalkulator di Android:
- Platform: Android
- Akses: Aplikasi Kalkulator bawaan pada perangkat Android atau aplikasi pihak ketiga.
- Cara Menggunakan:
  1. Buka aplikasi Kalkulator.
  2. Buka kalkulator ilmiah (biasanya dengan memutar perangkat ke mode lanskap atau menekan tombol menu).
  3. Masukkan nilai putaran (setelah mengkonversinya ke derajat, yaitu putaran
    – 360).
  4. Gunakan fungsi konversi derajat ke radian, yang biasanya ditandai dengan “deg” dan “rad”.
  5. Hasil konversi akan ditampilkan.
Desmos Scientific Calculator (Web):
- Platform: Web (dapat diakses melalui browser web apa pun)
- Akses: Kunjungi situs web Desmos.
- Cara Menggunakan:
  1. Buka Desmos Scientific Calculator.
  2. Gunakan fungsi kalkulator ilmiah untuk konversi putaran ke derajat, lalu ke radian.
  3. Masukkan nilai putaran (setelah mengkonversinya ke derajat, yaitu putaran
    – 360).
  4. Gunakan fungsi trigonometri dan konversi sudut untuk mendapatkan hasil dalam radian.

Rancangan Kalkulator Sederhana (HTML, CSS, JavaScript)

Berikut adalah rancangan sederhana untuk kalkulator konversi putaran ke radian:

Desain Antarmuka (HTML)

“`html Konversi Putaran ke Radian

body font-family: Arial, sans-serif; text-align: center; .container width: 300px; margin: 0 auto; padding: 20px; border: 1px solid #ccc; border-radius: 5px; input[type=”number”] width: 100%; padding: 10px; margin-bottom: 10px; box-sizing: border-box; button background-color: #4CAF50; color: white; padding: 10px 20px; border: none; border-radius: 5px; cursor: pointer; #result font-weight: bold;

Konversi Putaran ke Radian

Masukkan Putaran:

function convert() var revolutions = document.getElementById(“revolutions”).value; var radians = revolutions

2
Math.PI;

document.getElementById(“result”).innerHTML = “Hasil: ” + radians.toFixed(4) + ” radian”; “`

Logika Konversi (JavaScript)

Kode JavaScript di atas melakukan konversi putaran ke radian dengan rumus berikut:

radian = putaran

2

π

Fungsi `convert()` mengambil nilai input putaran, mengalikannya dengan 2
– π, dan menampilkan hasilnya dengan format 4 desimal.

Contoh Penggunaan

Contoh 1: Masukkan 1 putaran. Hasilnya akan menjadi sekitar 6.2832 radian.
Contoh 2: Masukkan 0.5 putaran. Hasilnya akan menjadi sekitar 3.1416 radian.
Contoh 3: Masukkan 2 putaran. Hasilnya akan menjadi sekitar 12.5664 radian.

Tabel Perbandingan

Fitur	Alat Bantu Konversi Online	Kalkulator iOS	Kalkulator Android	Desmos Scientific Calculator	Kalkulator Sederhana (HTML/JS)
Platform	Web	iOS	Android	Web	Web (dapat diakses di browser)
Kemudahan Penggunaan	Sangat mudah, antarmuka sederhana	Mudah, jika memahami langkah-langkah konversi	Mudah, jika memahami langkah-langkah konversi	Mudah, antarmuka intuitif	Mudah, antarmuka sederhana
Akurasi	Tinggi	Tinggi	Tinggi	Tinggi	Tinggi
Fitur Tambahan	Konversi berbagai satuan	Fungsi kalkulator ilmiah lainnya	Fungsi kalkulator ilmiah lainnya	Grafik dan visualisasi fungsi	Hanya konversi putaran ke radian
Kelebihan	Aksesibilitas luas, tidak perlu instalasi	Terintegrasi dengan perangkat, mudah digunakan	Terintegrasi dengan perangkat, mudah digunakan	Visualisasi, fleksibilitas	Sederhana, mudah dipahami
Kekurangan	Membutuhkan koneksi internet	Terbatas pada perangkat iOS	Terbatas pada perangkat Android	Membutuhkan koneksi internet	Fitur terbatas

Konversi Putaran ke Radian dalam Trigonometri

Trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga, sangat bergantung pada pengukuran sudut. Radian, sebagai satuan sudut, memainkan peran krusial dalam berbagai konsep trigonometri. Memahami konversi putaran ke radian adalah fondasi penting untuk menguasai topik ini. Artikel ini akan membahas secara mendalam tentang konversi putaran ke radian dalam konteks trigonometri, menguraikan konsep dasar, aplikasi dalam fungsi trigonometri, visualisasi grafik, dan contoh kasus nyata.

Pemahaman Konsep Dasar

Konsep dasar konversi putaran ke radian sangat penting untuk dipahami. Berikut adalah penjelasan detailnya:

Definisi Putaran dan Radian: Putaran adalah satuan sudut yang merepresentasikan satu putaran penuh, atau 360 derajat. Radian, di sisi lain, adalah satuan sudut yang didefinisikan berdasarkan panjang busur lingkaran. Satu radian adalah besar sudut pusat lingkaran yang panjang busurnya sama dengan jari-jari lingkaran tersebut.
Hubungan Matematis: Hubungan antara putaran dan radian sangatlah presisi. Satu putaran penuh setara dengan 2π radian. Ini berarti jika kita memiliki lingkaran dengan jari-jari r, maka keliling lingkaran adalah 2πr. Sudut pusat yang mencakup seluruh keliling lingkaran adalah 2π radian.
Konversi Sudut: Konversi sudut dari derajat ke radian dan sebaliknya melibatkan penggunaan faktor konversi. Untuk mengubah derajat ke radian, kita kalikan nilai derajat dengan π/180. Sebaliknya, untuk mengubah radian ke derajat, kita kalikan nilai radian dengan 180/π.

Berikut adalah contoh konversi sudut:

Contoh 1: Konversikan 45° ke radian.

45°
– (π/180°) = π/4 radian
Contoh 2: Konversikan π/3 radian ke derajat.

(π/3)
– (180°/π) = 60°
Contoh 3: Konversikan sudut tumpul 120° ke radian.

120°
– (π/180°) = (2π/3) radian
Contoh 4: Konversikan sudut refleks 300° ke radian.

300°
– (π/180°) = (5π/3) radian
Contoh 5: Konversikan sudut lebih dari 360°, misalnya 450°, ke radian.

450°
– (π/180°) = (5π/2) radian

Berikut adalah tabel yang merangkum konversi sudut-sudut istimewa:

Derajat (°)	Radian
0°	0
30°	π/6
45°	π/4
60°	π/3
90°	π/2
120°	2π/3
135°	3π/4
150°	5π/6
180°	π
270°	3π/2
360°	2π

Aplikasi dalam Fungsi Trigonometri

Radian sangat penting dalam aplikasi fungsi trigonometri. Berikut adalah penjelasannya:

Radian sebagai Argumen: Dalam fungsi trigonometri seperti sinus (sin), kosinus (cos), tangen (tan), kotangen (cot), sekan (sec), dan kosekan (csc), radian digunakan sebagai argumen (input). Ini berarti nilai sudut yang dimasukkan ke dalam fungsi-fungsi ini harus dalam satuan radian.
Perhitungan Nilai Fungsi Trigonometri: Untuk menghitung nilai fungsi trigonometri, sudut harus dalam radian.
- Contoh 1: Hitung sin(π/2).
  
  sin(π/2) = 1
- Contoh 2: Hitung cos(π).
  
  cos(π) = -1
- Contoh 3: Hitung tan(π/4).
  
  tan(π/4) = 1
Penggunaan Identitas Trigonometri: Identitas trigonometri dasar, seperti sin²θ + cos²θ = 1, tetap berlaku ketika sudut θ dinyatakan dalam radian.
- Contoh: Buktikan identitas sin²(π/6) + cos²(π/6) = 1.
  
  sin(π/6) = 1/2, cos(π/6) = √3/2
  (1/2)² + (√3/2)² = 1/4 + 3/4 = 1
Sifat Periodik Fungsi Trigonometri: Fungsi trigonometri bersifat periodik, yang berarti nilainya berulang setelah interval tertentu. Radian memainkan peran penting dalam menentukan periode fungsi-fungsi ini. Misalnya, fungsi sinus dan kosinus memiliki periode 2π, yang berarti nilai fungsi berulang setiap 2π radian. Fungsi tangen memiliki periode π.

Visualisasi Grafik

Visualisasi grafik fungsi trigonometri dengan radian pada sumbu x membantu dalam memahami perilaku fungsi.

Grafik Sinus (sin x): Grafik fungsi sinus (sin x) memiliki bentuk gelombang yang berosilasi antara -1 dan 1. Pada sumbu x, titik potong dengan sumbu x terjadi pada kelipatan π (…, -π, 0, π, 2π, …). Titik puncak terjadi pada π/2, 5π/2, dst, dan titik lembah terjadi pada 3π/2, 7π/2, dst.
Grafik Kosinus (cos x): Grafik fungsi kosinus (cos x) juga memiliki bentuk gelombang yang berosilasi antara -1 dan 1. Namun, grafik ini bergeser relatif terhadap grafik sinus. Titik potong dengan sumbu x terjadi pada π/2, 3π/2, 5π/2, dst. Titik puncak terjadi pada 0, 2π, 4π, dst, dan titik lembah terjadi pada π, 3π, dst.
Grafik Tangen (tan x): Grafik fungsi tangen (tan x) memiliki bentuk yang berbeda. Fungsi ini memiliki asimtot vertikal pada kelipatan ganjil π/2 (…, -3π/2, -π/2, π/2, 3π/2, …). Grafik memotong sumbu x pada kelipatan π (…, -π, 0, π, 2π, …).
Ilustrasi Grafik:
- Sumbu x diberi label dengan radian (0, π/2, π, 3π/2, 2π, dst).
- Grafik sinus (sin x) digambarkan dengan warna biru. Titik potong sumbu x ditandai dengan jelas.
- Grafik kosinus (cos x) digambarkan dengan warna merah. Titik puncak dan lembah ditandai.
- Grafik tangen (tan x) digambarkan dengan warna hijau. Asimtot vertikal dan titik potong sumbu x ditandai.
- Keterangan (legend) jelas menunjukkan warna yang sesuai dengan fungsi (sin x, cos x, tan x).

Contoh Kasus & Pemecahan Masalah

Berikut adalah contoh kasus nyata yang memerlukan konversi putaran ke radian:

Contoh Kasus: Gerakan Melingkar
- Deskripsi: Sebuah roda berputar dengan kecepatan konstan. Kita ingin menghitung jarak yang ditempuh oleh suatu titik pada tepi roda setelah beberapa putaran.
- Informasi yang Diketahui:
  - Jari-jari roda (r) = 0.5 meter
  - Jumlah putaran = 2.5 putaran
- Langkah Penyelesaian:
  1. Konversi putaran ke radian: 2.5 putaran
    
    2π radian/putaran = 5π radian
  2. Hitung jarak yang ditempuh: Jarak = r
    - θ = 0.5 meter
    - 5π = 2.5π meter ≈ 7.85 meter
  3. Kesimpulan: Titik pada tepi roda menempuh jarak sekitar 7.85 meter.
Variasi Contoh Kasus:
- Mudah: Hitung sudut dalam radian yang ditempuh oleh jarum jam dalam 30 menit. (Jawab: π radian)
- Sedang: Sebuah roda gigi berputar dengan kecepatan 120 putaran per menit. Hitung kecepatan sudut dalam radian per detik. (Jawab: 4π rad/s)
- Sulit: Sebuah benda bergerak melingkar dengan percepatan sudut konstan. Diketahui kecepatan sudut awal, percepatan sudut, dan waktu. Hitung sudut yang ditempuh dalam radian.
Kesalahan dalam Konversi Satuan: Kesalahan dalam konversi satuan dapat memengaruhi hasil akhir secara signifikan. Misalnya, jika kita salah menganggap putaran sebagai derajat, hasil perhitungan akan sangat berbeda dan tidak akurat. Penting untuk selalu memastikan konversi satuan dilakukan dengan benar.

Penggunaan dalam Perangkat Lunak dan Pemrograman

Konversi putaran ke radian merupakan operasi matematika fundamental yang memiliki aplikasi luas dalam dunia perangkat lunak dan pemrograman. Kemampuannya untuk mengubah satuan sudut dari format yang mudah dipahami manusia (putaran) ke format yang lebih cocok untuk perhitungan matematis (radian) menjadikannya krusial dalam berbagai bidang. Mari kita selami lebih dalam bagaimana konversi ini diimplementasikan dan dimanfaatkan dalam berbagai konteks pemrograman.

Implementasi dalam Bahasa Pemrograman

Berbagai bahasa pemrograman menyediakan fungsi bawaan atau pustaka untuk memudahkan konversi putaran ke radian. Hal ini menyederhanakan proses dan mengurangi potensi kesalahan dalam perhitungan. Proses konversi biasanya melibatkan penggunaan konstanta matematika π (pi) dan rumus dasar yang telah kita pahami sebelumnya. Mari kita lihat bagaimana ini diimplementasikan dalam beberapa bahasa pemrograman populer.

Python: Python, dengan kesederhanaan dan popularitasnya, menawarkan kemudahan dalam konversi. Modul math menyediakan konstanta pi yang diperlukan. Konversi putaran ke radian dilakukan dengan mengalikan jumlah putaran dengan 2π.
C++: Bahasa C++ juga menyediakan fasilitas serupa melalui pustaka cmath. Pengembang dapat menggunakan konstanta M_PI (atau std::numbers::pi dalam C++17 dan yang lebih baru) untuk perhitungan yang akurat.
JavaScript: Dalam JavaScript, konstanta Math.PI digunakan untuk perhitungan yang sama. Bahasa ini sering digunakan dalam pengembangan web dan game, sehingga konversi sudut menjadi sangat penting.

Contoh Kode Program Python

Berikut adalah contoh kode program sederhana dalam Python yang mengilustrasikan konversi putaran ke radian:

import math

def putaran_ke_radian(putaran):
  """Mengonversi putaran ke radian."""
  radian = putaran
- 2
- math.pi
  return radian

# Contoh penggunaan
jumlah_putaran = 0.5
radian_hasil = putaran_ke_radian(jumlah_putaran)
print(f"jumlah_putaran putaran sama dengan radian_hasil radian")

Kode ini mendefinisikan fungsi putaran_ke_radian yang mengambil jumlah putaran sebagai input dan mengembalikan nilai radian yang setara. Contoh penggunaan menunjukkan bagaimana fungsi ini dapat diterapkan untuk mengonversi 0.5 putaran.

Penggunaan dalam Pengembangan Game dan Simulasi, Cara mengubah putaran ke radian

Konversi putaran ke radian sangat penting dalam pengembangan game dan simulasi, terutama dalam menangani rotasi objek. Sistem game sering menggunakan sudut dalam radian untuk perhitungan matematika yang efisien. Misalnya, dalam animasi karakter, rotasi sendi karakter (seperti lengan atau kaki) seringkali didefinisikan dalam radian. Penggunaan radian memungkinkan perhitungan yang lebih akurat dan konsisten dalam berbagai sistem koordinat. Selain itu, dalam simulasi fisika, seperti simulasi gerakan benda, sudut dalam radian digunakan untuk menghitung kecepatan sudut, percepatan sudut, dan momen inersia.

Mengubah putaran ke radian adalah kunci dalam banyak perhitungan trigonometri, sama pentingnya dengan memahami bagaimana cara mengelola keuangan digital. Nah, berbicara soal keuangan, pernahkah Anda bertanya-tanya bagaimana cara mencairkan dana dari PayPal ke rekening bank lokal? Prosesnya sebenarnya cukup mudah, dan Anda bisa mempelajari langkah-langkahnya secara detail di cara kirim paypal ke dana. Setelah urusan keuangan beres, kembali lagi ke matematika: Ingat, konversi putaran ke radian akan membuka pintu bagi pemahaman yang lebih dalam tentang konsep sudut dan gerakan.

Animasi Objek: Dalam game, rotasi objek (misalnya, mobil berputar atau karakter berbalik) sering dihitung menggunakan radian.
Simulasi Fisika: Dalam simulasi fisika, radian digunakan untuk menghitung gerakan rotasi, seperti roda yang berputar atau planet yang mengorbit.
Kamera: Sudut pandang kamera seringkali dikontrol menggunakan radian untuk menghasilkan tampilan yang realistis.

Kasus Penggunaan dalam Perangkat Lunak Desain

Perangkat lunak desain, seperti CAD (Computer-Aided Design) dan perangkat lunak pemodelan 3D, secara ekstensif menggunakan konversi putaran ke radian. Dalam desain, objek seringkali perlu diputar atau diorientasikan dalam ruang 3D. Radian digunakan untuk menentukan sudut rotasi dengan presisi tinggi. Ini memastikan bahwa objek ditempatkan dan diorientasikan dengan benar. Konversi ini juga penting dalam manipulasi model, seperti memutar bagian-bagian model untuk melihat dari berbagai sudut atau membuat animasi.

Rotasi Objek: Desainer menggunakan radian untuk memutar objek 3D dengan presisi.
Orientasi Model: Radian digunakan untuk menentukan orientasi model dalam ruang 3D.
Animasi: Dalam animasi, radian digunakan untuk mengontrol gerakan dan rotasi objek sepanjang waktu.

Konversi Putaran ke Radian dalam Kehidupan Nyata

Konversi putaran ke radian bukanlah konsep abstrak yang hanya relevan dalam buku teks matematika. Sebaliknya, ia memiliki aplikasi praktis yang luas dan mendalam dalam berbagai aspek kehidupan kita, dari industri manufaktur hingga aktivitas sehari-hari. Memahami konversi ini memungkinkan kita untuk lebih memahami dunia di sekitar kita, mengoptimalkan kinerja dalam berbagai bidang, dan memecahkan masalah dengan lebih efisien.

Contoh Nyata Penggunaan Konversi Putaran ke Radian

Konversi putaran ke radian memainkan peran penting dalam berbagai bidang. Beberapa contoh nyata meliputi:

Teknik Mesin: Dalam desain dan analisis sistem mekanik, seperti mesin dan roda gigi, konversi ini digunakan untuk menghitung kecepatan sudut, percepatan sudut, dan posisi sudut. Hal ini sangat penting untuk memastikan kinerja yang optimal dan mencegah kerusakan.
Robotika: Robot menggunakan sensor dan aktuator yang seringkali bekerja berdasarkan putaran. Konversi ke radian diperlukan untuk mengontrol gerakan robot secara presisi, mulai dari pergerakan lengan hingga rotasi roda.
Navigasi: Sistem navigasi, seperti GPS dan sistem inertial, menggunakan konversi putaran ke radian untuk menghitung orientasi dan posisi. Ini penting untuk mengarahkan pesawat terbang, kapal, dan kendaraan lainnya.
Animasi dan Game: Dalam pembuatan animasi dan game, konversi ini digunakan untuk mengontrol rotasi objek, pergerakan kamera, dan efek visual lainnya.

Penggunaan dalam Industri Otomotif

Industri otomotif sangat bergantung pada konversi putaran ke radian dalam berbagai aspek, termasuk:

Pengendalian Mesin: Sistem manajemen mesin (ECU) menggunakan sensor untuk memantau kecepatan putaran poros engkol (crankshaft) dan poros bubungan (camshaft). Data ini kemudian dikonversi ke radian untuk menghitung waktu pengapian, injeksi bahan bakar, dan variabel penting lainnya untuk mengoptimalkan kinerja mesin.
Sistem Rem Anti-lock (ABS): Sensor pada roda mengukur kecepatan putaran roda. Informasi ini, yang seringkali dalam putaran per menit (RPM), dikonversi ke radian per detik untuk menentukan apakah roda terkunci selama pengereman. Jika roda terkunci, sistem ABS akan melepaskan rem untuk mencegah selip dan mempertahankan kontrol.
Sistem Kemudi Elektronik: Sensor sudut kemudi mengukur sudut putaran roda kemudi. Data ini kemudian dikonversi ke radian untuk mengontrol sistem kemudi elektronik, yang membantu pengemudi mengendalikan kendaraan dengan lebih mudah dan aman.
Transmisi Otomatis: Sensor pada transmisi mengukur kecepatan putaran berbagai komponen. Konversi ke radian digunakan untuk menentukan rasio gigi yang optimal untuk efisiensi bahan bakar dan kinerja.

Penggunaan dalam Olahraga

Konversi putaran ke radian juga memiliki aplikasi dalam olahraga, terutama dalam analisis gerakan dan kinerja atletik. Contohnya:

Putaran Roda Sepeda: Kecepatan putaran roda sepeda diukur dalam putaran per menit (RPM). Konversi ke radian per detik memungkinkan perhitungan kecepatan linier sepeda, yang penting untuk mengukur kinerja dan merencanakan strategi balapan. Misalnya, jika roda sepeda berputar pada 100 RPM dan jari-jari roda adalah 0.3 meter, maka kecepatan linier sepeda dapat dihitung.
Analisis Gerakan Atletik: Dalam olahraga seperti senam, atletik, dan seluncur indah, konversi putaran ke radian digunakan untuk menganalisis gerakan rotasi tubuh atlet. Ini membantu pelatih dan atlet untuk mengoptimalkan teknik dan meningkatkan kinerja. Misalnya, dalam senam, gerakan seperti putaran palang tunggal dianalisis menggunakan konversi ini untuk mengukur kecepatan rotasi dan sudut putaran.
Golf: Dalam analisis pukulan golf, konversi putaran ke radian dapat digunakan untuk menganalisis kecepatan putaran kepala stik golf saat mengenai bola, yang berdampak pada jarak dan lintasan bola.

Cerita Pendek: Petualangan Arloji Tua

Di sebuah kota kecil yang tenang, hiduplah sebuah arloji tua bernama Chronos. Chronos adalah arloji saku kuno dengan jarum jam, menit, dan detik yang berputar dengan anggun. Setiap pagi, seorang mekanik bernama Bapak Wijaya akan memutar tuas untuk memutar pegas utama Chronos. Bapak Wijaya selalu menggunakan konversi putaran ke radian untuk memastikan Chronos berdetak dengan tepat.

Suatu hari, Chronos berhenti berdetak. Bapak Wijaya, dengan bantuan putaran dan radian, menemukan bahwa pegas utama telah putus. Dia menghitung jumlah putaran yang diperlukan untuk mengganti pegas baru, menggunakan konversi untuk memastikan pegas dipasang dengan benar. Setelah diperbaiki, Chronos kembali berdetak, berputar dengan presisi yang tak tertandingi. Setiap putaran jarum detik, setiap sudut yang dibentuk oleh jarum jam, semuanya diatur oleh prinsip-prinsip konversi putaran ke radian.

Chronos, arloji tua yang bijaksana, terus berdetak, menjadi pengingat akan pentingnya matematika dalam kehidupan sehari-hari.

Tantangan dan Pengembangan Lanjutan

Setelah memahami dasar-dasar konversi putaran ke radian, siswa seringkali menghadapi tantangan yang lebih kompleks dalam mengaplikasikan konsep ini. Bagian ini akan membahas tantangan utama, strategi peningkatan pemahaman, topik lanjutan, dan sumber daya tambahan untuk memperdalam pengetahuan.

Oke, mari kita mulai. Mengubah putaran ke radian itu soal konversi sudut, kan? Tapi, pernahkah kamu merasa bingung saat mau ganti jasa pengiriman di Shopee? Sama seperti perhitungan sudut, memilih jasa yang tepat juga krusial. Nah, untungnya, cara mengganti jasa pengiriman di Shopee itu cukup mudah, mirip dengan cara kita mengkonversi putaran ke radian: butuh langkah yang tepat.

Jadi, setelah urusan pengiriman beres, kita bisa kembali fokus ke matematika sudut.

Identifikasi Tantangan Utama

Memahami konversi putaran ke radian bukanlah proses yang selalu mulus. Beberapa tantangan utama seringkali muncul bagi siswa yang baru mempelajari konsep ini.

Kesulitan dalam Memahami Konsep Dasar: Kesulitan seringkali muncul karena kurangnya pemahaman intuitif tentang radian itu sendiri. Siswa mungkin kesulitan membayangkan radian sebagai ukuran sudut berdasarkan panjang busur lingkaran.
Contoh Kesalahan: Seorang siswa mungkin salah mengira bahwa 1 putaran sama dengan 1 radian, atau mengabaikan faktor 2π dalam konversi.
Contoh Soal Pemicu Kesalahan:
1. Sebuah roda berputar sebanyak 3 putaran. Berapa radian sudut yang ditempuh roda tersebut?
2. Cara Mengidentifikasi Kesalahan: Perhatikan apakah siswa menggunakan rumus konversi yang benar (putaran x 2π = radian). Jika siswa hanya mengalikan dengan 1, atau menggunakan nilai yang salah, itu adalah indikasi kesalahan.
Kesulitan dalam Mengaplikasikan Konsep dalam Soal yang Lebih Kompleks: Siswa mungkin mengalami kesulitan saat menggabungkan konversi putaran ke radian dengan konsep-konsep lain seperti kecepatan sudut, percepatan sudut, atau momentum sudut.
Contoh Kesalahan: Siswa mungkin kesulitan mengidentifikasi variabel yang relevan dalam soal cerita yang kompleks.
Contoh Soal Pemicu Kesalahan:
1. Sebuah roda berputar dengan kecepatan 10 putaran per detik. Hitung kecepatan sudut roda dalam radian per detik.
2. Cara Mengidentifikasi Kesalahan: Perhatikan apakah siswa dapat mengidentifikasi kecepatan awal dalam putaran per detik, kemudian mengubahnya menjadi radian per detik.
Keterbatasan dalam Memvisualisasikan Konsep: Banyak siswa mengalami kesulitan memvisualisasikan hubungan antara putaran dan radian, terutama dalam konteks tiga dimensi.
Contoh Kesalahan: Siswa mungkin kesulitan membayangkan bagaimana sudut dalam radian berubah seiring dengan rotasi objek dalam ruang.
Contoh Soal Pemicu Kesalahan:
1. Sebuah benda berputar mengelilingi sumbu z. Jika benda tersebut berputar sebesar π/2 radian, bagaimana posisi akhirnya dibandingkan dengan posisi awalnya?
2. Cara Mengidentifikasi Kesalahan: Perhatikan apakah siswa dapat menghubungkan perubahan sudut dalam radian dengan perubahan posisi objek dalam ruang.

Strategi Peningkatan Pemahaman

Untuk mengatasi tantangan-tantangan ini, beberapa strategi pembelajaran dapat diterapkan untuk meningkatkan pemahaman siswa tentang konversi putaran ke radian.

Visualisasi: Menggunakan visualisasi untuk membantu siswa memahami konsep.
- Prinsip Pembelajaran: Visualisasi membantu siswa membangun representasi mental dari konsep abstrak.
- Contoh Penerapan: Menggunakan animasi atau simulasi interaktif yang menunjukkan bagaimana sudut dalam putaran dikonversi menjadi radian, dan bagaimana radian berhubungan dengan panjang busur lingkaran.
Latihan Berulang: Melakukan latihan berulang untuk memperkuat pemahaman.
- Prinsip Pembelajaran: Latihan berulang membantu siswa mengingat dan menerapkan rumus konversi dengan lebih cepat dan akurat.
- Contoh Penerapan: Memberikan siswa serangkaian soal latihan dengan tingkat kesulitan yang meningkat, mulai dari konversi sederhana hingga soal aplikasi yang lebih kompleks.
Penggunaan Analogi: Menggunakan analogi untuk mempermudah pemahaman.
- Prinsip Pembelajaran: Analogi membantu siswa menghubungkan konsep baru dengan pengetahuan yang sudah mereka miliki.
- Contoh Penerapan: Menjelaskan hubungan antara putaran dan radian dengan analogi jam, di mana satu putaran penuh sama dengan 2π radian (atau 360 derajat).

Topik Lanjutan & Aplikasinya

Konversi putaran ke radian menjadi dasar untuk memahami konsep-konsep fisika dan rekayasa yang lebih lanjut.

Kecepatan Sudut:
- Definisi: Kecepatan sudut (ω) adalah laju perubahan sudut suatu objek terhadap waktu. Satuan kecepatan sudut adalah radian per detik (rad/s).
- Contoh Soal: Sebuah roda berputar sebanyak 10 putaran dalam 2 detik. Berapakah kecepatan sudut roda tersebut?
- Penyelesaian:
  - Ubah putaran menjadi radian: 10 putaran
    – 2π rad/putaran = 20π rad.
  - Hitung kecepatan sudut: ω = perubahan sudut / waktu = 20π rad / 2 s = 10π rad/s.
- Aplikasi: Digunakan dalam perhitungan kecepatan rotasi mesin, roda gigi, dan sistem rotasi lainnya.
Percepatan Sudut:
- Definisi: Percepatan sudut (α) adalah laju perubahan kecepatan sudut suatu objek terhadap waktu. Satuan percepatan sudut adalah radian per detik kuadrat (rad/s²).
- Contoh Soal: Sebuah roda awalnya diam, kemudian dipercepat hingga mencapai kecepatan sudut 10π rad/s dalam waktu 5 detik. Berapakah percepatan sudut roda tersebut?
- Penyelesaian: α = (perubahan kecepatan sudut) / waktu = (10π rad/s – 0 rad/s) / 5 s = 2π rad/s².
- Aplikasi: Digunakan dalam analisis gerakan rotasi pada mesin, kendaraan, dan sistem mekanik lainnya.
Momentum Sudut:
- Definisi: Momentum sudut (L) adalah ukuran kelembaman rotasi suatu objek. Didefinisikan sebagai hasil kali momen inersia (I) dan kecepatan sudut (ω). Satuan momentum sudut adalah kg⋅m²/s.
- Contoh Soal: Sebuah roda memiliki momen inersia 2 kg⋅m² dan berputar dengan kecepatan sudut 5π rad/s. Berapakah momentum sudut roda tersebut?
- Penyelesaian: L = Iω = (2 kg⋅m²)
  – (5π rad/s) = 10π kg⋅m²/s.
- Aplikasi: Digunakan dalam analisis stabilitas rotasi, seperti pada gasing, roda sepeda, dan gerakan planet.

Sumber Daya Tambahan

Berikut adalah beberapa sumber daya tambahan yang dapat membantu siswa dalam mempelajari konversi putaran ke radian:

Video Tutorial:
- YouTube: “Radians, Degrees, and Angles” dari Khan Academy.
- Deskripsi: Video ini memberikan penjelasan visual yang jelas tentang perbedaan antara radian dan derajat, serta bagaimana melakukan konversi.
Artikel/Buku Teks:
- Buku Teks: “Fisika untuk Sains dan Teknik” oleh Halliday, Resnick, dan Walker.
- Deskripsi: Buku ini menyediakan penjelasan mendalam tentang konsep-konsep fisika, termasuk rotasi dan sudut.
Kuis/Latihan Interaktif:
- Situs Web: Math is Fun (mathsisfun.com).
- Deskripsi: Menyediakan kuis interaktif yang memungkinkan siswa untuk melatih keterampilan konversi mereka.
Forum Diskusi:
- Forum: Physics Forums (physicsforums.com).
- Deskripsi: Forum ini menyediakan platform untuk siswa untuk bertanya dan berdiskusi tentang konsep-konsep fisika, termasuk konversi sudut.
Contoh Soal dan Kunci Jawaban:
- Sumber: Bank soal fisika SMA dari berbagai sumber.
- Deskripsi: Menyediakan contoh soal yang bervariasi dengan kunci jawaban yang detail, memungkinkan siswa untuk menguji pemahaman mereka.

Terakhir

Dari mekanika hingga animasi, konversi putaran ke radian adalah keterampilan fundamental. Dengan memahami konsep dasar, rumus, dan aplikasi praktisnya, Anda telah membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita. Ingatlah, bahwa setiap putaran adalah perjalanan, dan setiap radian adalah langkah kecil menuju pemahaman yang lebih besar. Teruslah menjelajah, teruslah belajar, dan teruslah menerapkan pengetahuan ini dalam petualangan Anda.