Cara menulis rumus mtk di word – Tertarik untuk menguasai seni menulis rumus matematika yang rapi dan akurat di Microsoft Word? Bayangkan, Anda seorang pelajar yang ingin menyajikan pekerjaan rumah dengan sempurna, atau seorang guru yang ingin membuat soal ujian yang mudah dipahami. Mungkin Anda seorang profesional yang memerlukan dokumentasi teknis yang presisi. Kemampuan menulis rumus matematika di Word adalah kunci untuk membuka pintu menuju efisiensi dan profesionalisme.
Artikel ini akan membahas secara mendalam bagaimana cara menulis rumus matematika di Word, mulai dari dasar-dasar hingga teknik tingkat lanjut. Dari mengakses fitur Equation hingga menyisipkan simbol-simbol rumit, kita akan menjelajahi setiap aspek yang diperlukan untuk menguasai keterampilan ini. Bersiaplah untuk mengubah cara Anda berinteraksi dengan matematika di Word!
Menguasai Rumus Matematika di Word: Kunci Sukses di Era Digital
Pernahkah Anda merasa kesulitan saat menyusun laporan, makalah, atau presentasi yang membutuhkan simbol dan rumus matematika? Di era digital ini, kemampuan untuk menulis rumus matematika dengan mudah dan efisien di Microsoft Word bukan lagi sekadar keterampilan tambahan, melainkan sebuah kebutuhan. Artikel ini akan membahas betapa krusialnya kemampuan ini bagi berbagai kalangan, dari pelajar hingga profesional, serta memberikan panduan praktis untuk menguasainya.
Kemampuan menulis rumus matematika di Word membuka pintu menuju penyusunan dokumen yang lebih profesional, mudah dipahami, dan akurat. Mari kita selami lebih dalam mengapa kemampuan ini begitu penting.
Pentingnya Kemampuan Menulis Rumus Matematika di Word
Kemampuan menulis rumus matematika di Word sangat penting karena beberapa alasan krusial. Ini tidak hanya mempermudah penulisan dokumen ilmiah, tetapi juga meningkatkan kualitas komunikasi dan pemahaman konsep matematika.
- Bagi Pelajar: Mempermudah penyusunan tugas, laporan, dan ujian yang melibatkan rumus matematika. Ini meningkatkan efisiensi dan akurasi, serta memungkinkan pelajar fokus pada pemahaman konsep daripada kesulitan teknis penulisan.
- Bagi Guru: Memungkinkan pembuatan soal ujian, materi ajar, dan lembar kerja yang lebih profesional dan mudah dibaca. Guru dapat dengan mudah menyajikan rumus-rumus kompleks tanpa kesulitan.
- Bagi Profesional: Penting bagi berbagai profesi seperti ilmuwan, insinyur, analis keuangan, dan data scientist. Kemampuan ini memfasilitasi penulisan laporan penelitian, analisis data, dan presentasi yang membutuhkan notasi matematika.
Profesi dan Situasi yang Membutuhkan Kemampuan Ini
Kemampuan menulis rumus matematika di Word sangat dibutuhkan dalam berbagai profesi dan situasi. Berikut adalah beberapa contoh spesifik:
- Ilmuwan dan Peneliti: Menulis publikasi ilmiah, laporan penelitian, dan presentasi yang melibatkan persamaan dan model matematika yang kompleks.
- Insinyur: Membuat laporan desain, analisis struktural, dan perhitungan teknis yang memerlukan notasi matematika yang akurat.
- Analis Keuangan: Menyusun laporan keuangan, model investasi, dan analisis risiko yang melibatkan rumus-rumus finansial.
- Data Scientist: Menulis laporan analisis data, model statistik, dan presentasi yang membutuhkan representasi matematis dari data.
- Guru Matematika: Membuat soal ujian, materi ajar, dan lembar kerja yang melibatkan rumus matematika.
- Mahasiswa: Menyusun tugas, makalah, dan skripsi yang melibatkan rumus matematika.
Manfaat Menguasai Cara Menulis Rumus Matematika di Word
Menguasai cara menulis rumus matematika di Word memberikan sejumlah manfaat signifikan:
- Meningkatkan Efisiensi: Mempermudah dan mempercepat proses penulisan dokumen yang melibatkan rumus matematika.
- Meningkatkan Akurasi: Mengurangi risiko kesalahan dalam penulisan rumus, sehingga memastikan keakuratan informasi.
- Meningkatkan Profesionalisme: Menghasilkan dokumen yang terlihat lebih rapi, profesional, dan mudah dibaca.
- Mempermudah Komunikasi: Memungkinkan komunikasi yang lebih efektif dalam bidang yang melibatkan matematika.
- Meningkatkan Pemahaman: Membantu dalam memahami dan mengaplikasikan konsep matematika dengan lebih baik.
Sebagai contoh, seorang insinyur yang sedang membuat laporan desain jembatan dapat dengan mudah menyertakan persamaan struktural yang kompleks dalam laporannya. Seorang analis keuangan dapat dengan cepat membuat model investasi dengan rumus-rumus yang akurat. Seorang guru matematika dapat membuat soal ujian yang lebih menarik dan mudah dipahami oleh siswa.
Memahami Antarmuka Word untuk Rumus Matematika

Source: microsoftword.id
Menulis rumus matematika di Word memang bisa jadi tantangan, tapi dengan sedikit trik, semuanya jadi lebih mudah. Bayangkan, sama seperti saat kita belajar memahami struktur dasar HTML, CSS, dan JavaScript untuk membangun sebuah website. Memang, awalnya rumit, namun dengan ketekunan, kita bisa menguasainya, sama seperti kita bisa membuat website impian kita dengan membaca artikel tentang cara membuat website dengan coding.
Nah, kembali ke Word, penggunaan Equation Editor atau bahkan shortcut keyboard, akan membuat penulisan rumus matematika menjadi jauh lebih efisien.
Menulis rumus matematika di Microsoft Word bisa jadi tantangan, tetapi dengan pemahaman yang tepat tentang antarmuka dan fitur yang tersedia, proses ini dapat disederhanakan. Bagian ini akan membahas secara mendalam tentang bagaimana mengakses dan memanfaatkan berbagai elemen dalam Word untuk membuat rumus matematika yang akurat dan profesional.
Akses Fitur “Equation” atau “Rumus” di Berbagai Versi Word
Fitur “Equation” atau “Rumus” adalah kunci untuk menuliskan persamaan matematika di Word. Aksesnya sedikit berbeda tergantung pada versi Word yang Anda gunakan.
- Word 2007 dan versi sebelumnya: Fitur rumus biasanya ditemukan di menu “Insert” (Sisipkan), lalu pilih “Object” (Objek). Di jendela yang muncul, pilih “Microsoft Equation 3.0”.
- Word 2010, 2013, 2016, dan 2019: Fitur rumus terletak di tab “Insert” (Sisipkan) pada grup “Symbols” (Simbol). Klik tombol “Equation” (Rumus) untuk memulai, atau klik panah bawah pada tombol untuk melihat opsi rumus bawaan.
- Word untuk Microsoft 365: Prosesnya serupa dengan versi 2010 ke atas, dengan peningkatan pada antarmuka dan penambahan fitur yang lebih modern. Perhatikan bahwa Microsoft 365 seringkali mendapatkan pembaruan fitur lebih dulu.
Perbedaan utama terletak pada penempatan tombol dan fitur tambahan. Versi yang lebih baru menawarkan antarmuka yang lebih intuitif dan template rumus yang lebih banyak. Perbedaan ini tidak terlalu signifikan dalam hal fungsionalitas dasar, tetapi dapat mempengaruhi efisiensi dan kemudahan penggunaan.
Bagian Penting dalam Antarmuka “Equation”
Antarmuka “Equation” menyediakan berbagai elemen untuk menyusun rumus matematika. Memahami bagian-bagian ini sangat penting untuk penulisan rumus yang efektif.
- Simbol: Bagian ini berisi berbagai simbol matematika, termasuk operator (+, -, ×, ÷), simbol relasi (=, ≠, ), simbol Yunani (α, β, γ), dan banyak lagi. Simbol-simbol ini dikelompokkan berdasarkan kategori untuk memudahkan pencarian.
- Template: Template menyediakan struktur dasar untuk rumus, seperti pecahan, akar kuadrat, integral, matriks, dan lain-lain. Template ini membantu pengguna menyusun rumus dengan cepat tanpa harus membangun struktur dari awal.
- Struktur: Bagian ini mencakup berbagai elemen struktur seperti kurung, indeks, limit, dan integral. Elemen-elemen ini digunakan untuk mengatur tampilan dan urutan operasi dalam rumus.
Memahami fungsi dari masing-masing bagian ini akan sangat membantu dalam menyusun rumus yang kompleks dan akurat.
Ikon-Ikon yang Sering Digunakan dalam Penulisan Rumus Matematika di Word
Beberapa ikon sering digunakan dalam penulisan rumus matematika di Word. Berikut adalah daftar beberapa ikon penting beserta fungsinya:
- Pecahan: Digunakan untuk membuat pecahan, dengan berbagai pilihan seperti pecahan biasa, pecahan bertumpuk, dan pecahan horizontal.
- Indeks dan Pangkat: Digunakan untuk menulis indeks (subskrip) dan pangkat (superscript), misalnya, x 2 atau x 2.
- Akar: Digunakan untuk membuat akar kuadrat, akar pangkat tiga, dan akar pangkat lainnya.
- Integral: Digunakan untuk membuat simbol integral, dengan berbagai pilihan seperti integral tak tentu dan integral tentu.
- Jumlah dan Produk: Digunakan untuk membuat simbol sigma (∑) untuk penjumlahan dan pi (∏) untuk perkalian.
- Kurung: Digunakan untuk menambahkan kurung ((), [], ) pada rumus.
- Matriks: Digunakan untuk membuat matriks dengan berbagai ukuran dan format.
- Limit: Digunakan untuk membuat simbol limit dalam kalkulus.
- Operator: Termasuk simbol-simbol matematika dasar seperti +, -, ×, ÷, =, ≠, .
Penguasaan ikon-ikon ini sangat penting untuk menulis berbagai jenis rumus matematika.
Menyesuaikan Ukuran dan Tampilan Rumus di Word
Word memungkinkan penyesuaian ukuran dan tampilan rumus agar sesuai dengan kebutuhan.
- Ukuran: Ukuran rumus dapat diubah dengan mengubah ukuran font. Pilih seluruh rumus atau bagian tertentu, lalu ubah ukuran font melalui tab “Home” (Beranda).
- Gaya: Gaya rumus dapat disesuaikan melalui opsi di tab “Design” (Desain) pada menu “Equation Tools”. Opsi ini memungkinkan perubahan pada jenis huruf, ukuran simbol, dan spasi.
- Penomoran Rumus: Word memungkinkan penomoran rumus secara otomatis. Klik kanan pada rumus dan pilih “Insert Caption” (Sisipkan Keterangan). Pilih label yang sesuai (misalnya, “Equation”) dan Word akan secara otomatis memberikan nomor pada rumus.
Dengan penyesuaian ini, pengguna dapat memastikan bahwa rumus terlihat jelas dan sesuai dengan standar penulisan ilmiah atau format dokumen yang diinginkan.
Menulis Pecahan, Akar, dan Pangkat
Menulis rumus matematika di Microsoft Word melibatkan lebih dari sekadar mengetik simbol. Pecahan, akar, dan pangkat adalah elemen fundamental dalam matematika yang memerlukan penanganan khusus agar tampilannya benar dan mudah dipahami. Panduan ini akan membahas secara mendalam cara menulis elemen-elemen tersebut dengan tepat di Word, memanfaatkan fitur yang tersedia dan memaksimalkan efisiensi penulisan.
Mari kita telusuri bagaimana cara menyajikan elemen-elemen matematika ini secara efektif.
Menulis Pecahan
Pecahan adalah representasi penting dalam matematika. Berikut adalah cara menulis pecahan dengan benar di Microsoft Word:
- Menulis Pecahan Biasa: Fitur “Equation” di Word menyediakan cara paling akurat untuk menulis pecahan. Berikut langkah-langkahnya:
- Buka tab “Insert” di ribbon Word.
- Klik tombol “Equation” di grup “Symbols”.
- Pilih template pecahan dari galeri yang muncul, atau ketikkan pecahan langsung dengan mengetikkan tanda garis miring (/) setelah angka pembilang. Word secara otomatis akan mengubahnya menjadi format pecahan.
- Isi pembilang dan penyebut sesuai dengan pecahan yang ingin ditulis.
- Menulis Pecahan Campuran: Pecahan campuran, seperti 2 1/4, membutuhkan penanganan spasi yang tepat. Gunakan spasi antara bilangan bulat dan pecahan. Fitur “Equation” juga sangat membantu di sini, terutama jika pecahan yang digunakan lebih kompleks.
- Shortcut Keyboard untuk Pecahan: Word menawarkan shortcut keyboard untuk mempercepat penulisan pecahan. Setelah membuka fitur “Equation”, Anda dapat menggunakan kombinasi keyboard tertentu untuk memasukkan simbol pecahan dengan cepat.
- Tabel Perbandingan Metode Penulisan Pecahan:
- Mengkonversi Pecahan ke Desimal dan Persentase: Untuk mengkonversi pecahan menjadi desimal, bagi pembilang dengan penyebut. Untuk persentase, kalikan hasil desimal dengan 100%. Tuliskan hasilnya di Word dengan format yang sesuai.
- Contoh Pecahan Kompleks: Untuk pecahan bersusun, gunakan fitur “Equation” dan template pecahan yang tersedia. Pastikan untuk menggunakan tanda kurung untuk mengelompokkan pecahan dengan benar dan memastikan urutan operasi yang tepat. Contoh:
Pecahan bersusun adalah contoh kompleksitas yang dapat diatasi dengan fitur equation.
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Garis Miring (/) | Cepat dan mudah untuk pecahan sederhana. | Tidak selalu menampilkan pecahan dengan benar, terutama untuk pecahan kompleks. |
| Fitur “Equation” | Menampilkan pecahan dengan presisi tinggi, mendukung pecahan kompleks, dan mudah diedit. | Membutuhkan beberapa langkah tambahan untuk memulai. |
| Simbol Fraksi (jika tersedia) | Cepat untuk simbol pecahan tertentu (misalnya, ½). | Terbatas pada simbol pecahan yang sudah ada. |
Menulis Akar Kuadrat
Akar kuadrat adalah operasi matematika penting. Berikut adalah cara menulisnya di Word:
- Menulis Simbol Akar Kuadrat:
- Menggunakan Simbol Khusus: Buka tab “Insert” -> “Symbol” -> “More Symbols”. Cari simbol akar kuadrat (√) dan sisipkan.
- Menggunakan Fitur “Equation”: Pilih template yang sesuai dari galeri “Equation”.
- Menulis Ekspresi Akar Kuadrat: Setelah menyisipkan simbol akar kuadrat, ketikkan angka atau ekspresi di bawah tanda akar. Pastikan radikan (angka di dalam akar) terletak dengan benar di bawah simbol akar. Gunakan fitur “Equation” untuk penempatan yang tepat.
- Akar Pangkat Tiga dan Lebih Tinggi: Fitur “Equation” memungkinkan penulisan akar pangkat tiga, empat, dan seterusnya. Gunakan template akar yang sesuai dan sesuaikan indeks (pangkat akar) sesuai kebutuhan.
- Ekspresi dengan Akar Kuadrat di dalam Pecahan atau Pangkat: Gunakan fitur “Equation” untuk menggabungkan akar kuadrat dengan pecahan dan pangkat. Pastikan untuk menggunakan tanda kurung untuk mengelompokkan ekspresi dengan benar.
- Contoh Kode atau Sintaks: Tidak ada kode khusus yang diperlukan. Cukup gunakan fitur “Equation” dan simbol yang tersedia.
- Mengatasi Masalah Tampilan Akar Kuadrat: Jika simbol akar terpotong atau tidak proporsional, sesuaikan ukuran font dan gunakan fitur “Equation” untuk memastikan tampilan yang benar.
Menulis Pangkat
Pangkat adalah operasi matematika yang krusial. Berikut adalah cara menuliskannya di Word:
- Menulis Pangkat dengan “Superscript” dan “Equation”:
- Superscript: Pilih angka atau ekspresi yang akan menjadi pangkat, lalu klik tombol “Superscript” (x²) di grup “Font” pada tab “Home”. Metode ini cocok untuk pangkat sederhana.
- “Equation”: Cara paling akurat. Gunakan template pangkat yang tersedia.
Perbandingan:
- “Superscript” cepat, tetapi terbatas pada pangkat sederhana.
- “Equation” lebih fleksibel dan akurat, terutama untuk pangkat kompleks.
- Menulis Pangkat Negatif dan Pecahan: Gunakan fitur “Equation” untuk menulis pangkat negatif (misalnya, x⁻²) dan pangkat pecahan (misalnya, x^(1/2)).
- Ekspresi yang Melibatkan Pangkat: Gunakan fitur “Equation” untuk menggabungkan pangkat dengan pecahan, akar, dan kombinasi lainnya.
- Tips dan Trik untuk Penulisan Pangkat:
- Gunakan shortcut keyboard untuk “Superscript” (Ctrl + Shift + +).
- Sesuaikan pengaturan default font untuk pangkat jika perlu.
- Menulis Notasi Ilmiah: Gunakan fitur “Equation” untuk menulis notasi ilmiah (misalnya, 1.23 x 10^4).
- Contoh Soal Matematika: Contoh soal dengan pangkat, akar, dan pecahan, beserta cara penulisannya yang benar di Word:
Soal matematika yang kompleks dapat ditulis dengan mudah menggunakan fitur equation.
Tips dan Trik Umum
- Memastikan Tampilan Rapi: Gunakan spasi yang tepat, sesuaikan ukuran font, dan atur posisi simbol untuk tampilan yang rapi.
- Menggunakan “Equation” untuk Persamaan Kompleks: Fitur “Equation” sangat berguna untuk membuat persamaan matematika yang kompleks dengan tampilan yang konsisten.
- Mengatasi Masalah Umum:
- Pastikan simbol ditempatkan dengan benar.
- Periksa tampilan setelah selesai mengetik.
- Gunakan fitur “Equation” untuk penyesuaian.
- Ilustrasi Perbedaan Tampilan:
Ilustrasi menunjukkan perbedaan tampilan sebelum dan sesudah menggunakan fitur “Equation”. Tampilan yang benar menggunakan fitur equation akan terlihat lebih rapi dan mudah dibaca, sementara tampilan yang salah (misalnya, menggunakan garis miring untuk pecahan atau superscript yang tidak tepat) akan terlihat kurang profesional.
- Contoh Soal Matematika:
- Hitung: (1/2 + 1/4)².
Solusi: (3/4)² = 9/16 - Sederhanakan: √25 + √16.
Solusi: 5 + 4 = 9 - Hitung: 2³ x (1/2)².
Solusi: 8 x 1/4 = 2 - Selesaikan: √(9 + 16).
Solusi: √25 = 5 - Hitung: (3/2)³ / 3².
Solusi: (27/8) / 9 = 3/8
Contoh soal ini menunjukkan penggunaan pecahan, akar, dan pangkat, serta solusi yang ditulis dengan benar di Word menggunakan fitur “Equation”.
- Hitung: (1/2 + 1/4)².
- Perbandingan dengan Software Lain:
Dibandingkan dengan LaTeX, Word mungkin kurang fleksibel untuk persamaan yang sangat kompleks, tetapi lebih mudah digunakan untuk pengguna awam. LaTeX menawarkan kontrol penuh, tetapi membutuhkan lebih banyak waktu untuk dipelajari. Software lain seperti MathType menawarkan fitur yang lebih spesifik untuk penulisan matematika, namun biasanya berbayar.
Menulis Rumus dengan Indeks dan Subskrip: Cara Menulis Rumus Mtk Di Word
Indeks dan subskrip adalah elemen penting dalam notasi matematika, memungkinkan kita untuk merepresentasikan berbagai konsep dengan presisi. Dalam Word, kemampuan untuk menulis indeks (pangkat) dan subskrip (indeks bawah) sangat penting untuk menyajikan rumus matematika secara akurat dan mudah dipahami. Kemampuan ini tidak hanya meningkatkan kejelasan visual tetapi juga memungkinkan representasi yang tepat dari konsep-konsep seperti eksponen, notasi kimia, dan elemen dalam matriks.
Menulis Indeks (Pangkat) dan Subskrip (Indeks Bawah)
Word menyediakan cara mudah untuk memasukkan indeks dan subskrip. Berikut adalah langkah-langkahnya:
- Menggunakan Tombol Pintas: Cara tercepat adalah dengan menggunakan tombol pintas. Untuk indeks, pilih teks yang ingin Anda jadikan pangkat, lalu tekan Ctrl + Shift + = (Windows) atau Command + Shift + = (Mac). Untuk subskrip, pilih teks yang ingin Anda jadikan indeks bawah, lalu tekan Ctrl + = (Windows) atau Command + = (Mac).
- Melalui Menu: Anda juga dapat menggunakan menu. Pilih teks yang ingin Anda ubah, lalu klik kanan dan pilih “Font”. Di jendela “Font”, centang kotak “Superskrip” (untuk indeks) atau “Subskrip” (untuk indeks bawah) di bagian “Efek”.
- Menggunakan Equation Editor: Cara lain adalah dengan menggunakan Equation Editor di Word. Buka Equation Editor (Insert > Equation), kemudian gunakan template yang tersedia untuk memasukkan indeks dan subskrip.
Contoh Penggunaan Indeks dan Subskrip
Indeks dan subskrip digunakan secara luas dalam berbagai bidang matematika dan sains. Berikut adalah beberapa contoh:
- Notasi Kimia: Dalam kimia, subskrip digunakan untuk menunjukkan jumlah atom dari suatu elemen dalam sebuah molekul. Misalnya, rumus molekul air adalah H 2O.
- Vektor: Dalam aljabar linear, indeks digunakan untuk menunjukkan komponen-komponen vektor. Misalnya, vektor a dapat ditulis sebagai a 1, a 2, a 3.
- Matriks: Dalam aljabar linear, indeks digunakan untuk mengidentifikasi elemen dalam matriks. Misalnya, elemen pada baris ke-i dan kolom ke-j dari matriks A ditulis sebagai A ij.
- Eksponen: Indeks digunakan untuk menunjukkan pangkat dalam ekspresi matematika. Misalnya, x 2 (x kuadrat).
- Turunan: Notasi turunan sering menggunakan indeks untuk membedakan turunan orde yang berbeda. Misalnya, f”(x) untuk turunan kedua dari f(x).
Latihan Soal
Untuk menguji pemahaman Anda, cobalah soal-soal berikut:
- Tuliskan rumus untuk luas lingkaran dengan jari-jari r: A = πr2.
- Tuliskan rumus molekul glukosa: C 6H 12O 6.
- Tuliskan elemen pada baris ke-2 dan kolom ke-3 dari matriks A: A 23.
- Tuliskan turunan pertama dari fungsi f(x): f'(x).
Demonstrasi Langkah demi Langkah Mengatur Posisi Indeks dan Subskrip
Mengatur posisi indeks dan subskrip dalam Word memerlukan beberapa langkah sederhana:
- Pilih Teks: Pilih teks yang ingin Anda jadikan indeks atau subskrip.
- Gunakan Tombol Pintas atau Menu: Gunakan tombol pintas (Ctrl + Shift + = untuk indeks, Ctrl + = untuk subskrip) atau buka jendela “Font” (klik kanan, pilih “Font”) dan centang “Superskrip” atau “Subskrip”.
- Penyesuaian (Opsional): Jika posisi indeks atau subskrip terlihat kurang pas, Anda dapat menyesuaikan posisi dan ukuran font secara manual di jendela “Font”. Anda dapat mengubah offset dan ukuran relatif untuk mendapatkan tampilan yang diinginkan.
- Menggunakan Equation Editor (Alternatif): Dalam Equation Editor, indeks dan subskrip biasanya sudah diatur posisinya secara otomatis. Anda dapat memilih template yang sesuai dan memasukkan nilai yang diinginkan. Jika perlu, Anda dapat menyesuaikan posisi secara manual melalui opsi yang tersedia di Equation Editor.
Menggunakan Kurung dan Tanda Kurung
Kurung dan tanda kurung adalah elemen krusial dalam penulisan rumus matematika. Mereka berfungsi untuk mengelompokkan ekspresi, menentukan urutan operasi, dan memastikan interpretasi yang tepat dari suatu rumus. Penggunaan yang tepat dari kurung dan tanda kurung sangat penting untuk menghindari ambiguitas dan memastikan kejelasan dalam komunikasi matematika.
Memasukkan dan Mengatur Kurung
Word menyediakan beberapa cara untuk memasukkan kurung dan tanda kurung dalam rumus matematika. Anda dapat menggunakan simbol kurung langsung dari keyboard, atau menggunakan fitur “Equation” di Word untuk memasukkan simbol kurung yang lebih kompleks. Pengaturan kurung melibatkan penyesuaian ukuran dan posisi agar sesuai dengan ekspresi yang dikurung.
- Menggunakan Keyboard: Kurung biasa seperti ( ), [ ], dan dapat langsung diketikkan.
- Menggunakan Equation Editor: Buka “Insert” > “Equation”. Di tab “Design”, Anda akan menemukan opsi kurung yang lebih beragam, termasuk kurung yang dapat diubah ukurannya secara otomatis sesuai dengan konten di dalamnya (misalnya, kurung besar untuk ekspresi pecahan atau akar).
- Menyesuaikan Ukuran: Setelah memasukkan kurung, Anda mungkin perlu menyesuaikan ukurannya agar sesuai dengan ekspresi di dalamnya. Ini dapat dilakukan dengan memilih kurung dan menggunakan opsi “Size” di tab “Design” Equation Editor.
- Posisi: Posisi kurung biasanya otomatis disesuaikan oleh Word, namun Anda dapat melakukan penyesuaian manual jika diperlukan, terutama untuk kurung yang kompleks atau bertingkat.
Tips Memastikan Tampilan Kurung yang Sesuai
Untuk memastikan kurung dan tanda kurung terlihat sesuai dengan kebutuhan matematika, perhatikan beberapa tips berikut:
- Pilih Jenis Kurung yang Tepat: Gunakan kurung biasa ( ) untuk pengelompokan standar, kurung siku [ ] untuk pengelompokan yang lebih jelas, dan kurung kurawal untuk himpunan atau notasi tertentu.
- Gunakan Kurung yang Dapat Disesuaikan Ukurannya: Untuk ekspresi yang panjang atau kompleks, gunakan kurung yang dapat menyesuaikan ukurannya secara otomatis. Ini memastikan kurung tidak terlalu kecil atau terlalu besar.
- Perhatikan Spasi: Pastikan ada cukup spasi antara kurung dan ekspresi di dalamnya agar rumus mudah dibaca.
- Periksa Konsistensi: Pastikan penggunaan kurung konsisten di seluruh rumus. Jangan mencampuradukkan jenis kurung tanpa alasan yang jelas.
Contoh Soal yang Melibatkan Kurung dan Tanda Kurung
Berikut adalah beberapa contoh soal yang melibatkan penggunaan kurung dan tanda kurung dalam berbagai jenis rumus:
- Aljabar: Sederhanakan ekspresi berikut: 2(x + 3)
(4x – 1).
- Pecahan: Hitung nilai dari: ((1/2) + (1/3)) / (1/4).
- Persamaan Kuadrat: Selesaikan persamaan kuadrat berikut: x 25x + 6 = 0. Gunakan rumus abc.
- Logaritma: Sederhanakan: log 2(8) + log 2(4).
Penyelesaian: 2x + 6 – 4x + 1 = -2x + 7
Penyelesaian: (5/6) / (1/4) = (5/6)
– 4 = 10/3
Penyelesaian: x = (-b ± √(b2
-4ac)) / 2a = (5 ± √(25 – 24)) / 2 = (5 ± 1) / 2, sehingga x = 3 atau x = 2Oke, mari kita mulai. Menulis rumus matematika di Word memang kadang bikin pusing, ya? Tapi tenang, ada caranya! Nah, ngomong-ngomong soal angka dan perhitungan, pernahkah kamu penasaran berapa lama kartu SIM-mu aktif? Sama seperti kita perlu rumus untuk matematika, kita juga bisa mencari tahu umur kartu Indosat kita, lho. Caranya?
Simak saja artikel ini: cara mengetahui umur kartu indosat. Kembali ke Word, dengan sedikit trik, kamu bisa membuat rumus matematika terlihat rapi dan mudah dipahami, tak kalah pentingnya dengan mengetahui masa aktif kartu.
Penyelesaian: log2(8) + log 2(4) = 3 + 2 = 5
Ilustrasi Pengaruh Kurung dan Tanda Kurung
Berikut adalah ilustrasi bagaimana kurung dan tanda kurung memengaruhi tampilan rumus:
- Tanpa Kurung: Misalkan kita memiliki ekspresi 2 + 3 x 4. Tanpa kurung, berdasarkan aturan urutan operasi (prioritas perkalian sebelum penjumlahan), hasilnya adalah 2 + 12 = 14.
- Dengan Kurung: Jika kita menulis (2 + 3) x 4, kurung mengubah urutan operasi. Pertama, kita menghitung 2 + 3 = 5, kemudian mengalikan hasilnya dengan 4, sehingga 5 x 4 = 20.
- Kurung Bersarang: Ekspresi seperti [2 + (3 x 4)] menunjukkan penggunaan kurung bersarang. Pertama, kita menghitung 3 x 4 = 12, kemudian menambahkan 2, sehingga hasilnya adalah 2 + 12 = 14. Kurung siku membantu memperjelas pengelompokan.
- Kurung dengan Pecahan: Dalam ekspresi ((1/2) + (1/3)) / (1/4), kurung memastikan bahwa penjumlahan pecahan (1/2) + (1/3) dilakukan terlebih dahulu sebelum dibagi dengan (1/4). Ini menghasilkan hasil yang berbeda jika tanpa kurung.
Menulis Rumus Kompleks (Integral, Limit, Matriks)
Dalam era digital, kemampuan menulis rumus matematika kompleks di Microsoft Word menjadi sangat krusial bagi siswa, mahasiswa, guru, dan profesional di berbagai bidang. Artikel ini akan membahas secara mendalam langkah-langkah, tips, dan contoh praktis untuk menguasai penulisan rumus integral, limit, dan matriks dengan efektif. Tujuannya adalah memberikan panduan komprehensif yang mudah diikuti, sehingga pengguna dapat dengan percaya diri menyajikan soal dan solusi matematika yang jelas dan akurat.
Oke, mari kita bedah. Menulis rumus matematika di Word memang kadang bikin pusing, ya? Tapi tenang, ada caranya! Nah, kalau sudah mahir, kemampuan ini sangat berguna, apalagi kalau kamu sedang mengerjakan tugas kuliah seperti membuat paper. Prosesnya akan jauh lebih mudah. Jangan lupa, untuk mempersiapkan paper yang baik, kamu bisa simak panduan lengkapnya di cara buat paper kuliah.
Setelah urusan paper selesai, kembali lagi ke Word. Dengan menguasai teknik menulis rumus, kamu bisa menyajikan hasil perhitungan dengan rapi dan profesional.
Mari kita selami lebih dalam cara menulis rumus-rumus kompleks tersebut di Word.
Langkah-langkah Menulis Rumus Kompleks di Word
Penulisan rumus matematika kompleks di Word sangat terbantu dengan penggunaan Equation Editor. Berikut adalah langkah-langkah detail untuk menggunakannya:
- Akses Equation Editor: Buka dokumen Word, lalu klik tab “Insert” pada ribbon. Di grup “Symbols”, klik tombol “Equation”. Equation Editor akan terbuka, biasanya dengan tampilan area untuk mengetik rumus dan tab “Design” yang berisi berbagai simbol dan struktur matematika.
- Memilih Struktur Rumus: Di tab “Design”, terdapat grup “Structures” yang berisi berbagai pilihan struktur rumus seperti pecahan, akar, integral, limit, matriks, dan kurung. Pilih struktur yang sesuai dengan rumus yang ingin ditulis.
- Memasukkan Simbol dan Karakter: Gunakan simbol-simbol matematika yang tersedia di grup “Symbols” atau ketik langsung karakter dan angka pada area pengetikan rumus.
- Mengatur Ukuran, Gaya, dan Spasi: Atur ukuran huruf, gaya huruf (misalnya, italic untuk variabel), dan spasi sesuai kebutuhan. Anda dapat melakukannya melalui tab “Design” atau dengan menggunakan shortcut keyboard.
- Menggunakan Shortcut Keyboard: Pelajari dan gunakan shortcut keyboard untuk mempercepat penulisan rumus. Beberapa shortcut umum meliputi:
- Ctrl+=: Memasukkan indeks ( subscript).
- Ctrl+Shift+=: Memasukkan pangkat ( superscript).
- / (slash) diikuti spasi: Membuat pecahan.
- \sqrt diikuti spasi: Membuat akar kuadrat.
- \int diikuti spasi: Membuat simbol integral.
- \lim diikuti spasi: Membuat limit.
- Mengatasi Kesalahan Umum:
- Kurung yang Tidak Sesuai: Pastikan kurung buka dan tutup sesuai. Gunakan struktur kurung yang tersedia di Equation Editor.
- Kesalahan Penulisan Simbol: Periksa kembali penulisan simbol matematika (misalnya, ∫, ∑, ∞) untuk memastikan keakuratannya.
- Kesalahan Spasi: Perhatikan spasi antar simbol dan angka untuk menghindari kebingungan.
Panduan Visual: (Karena keterbatasan format, panduan visual berupa deskripsi langkah-langkah. Ilustrasi visual sebenarnya akan sangat membantu.)
- Integral:
- Klik “Equation” untuk membuka Equation Editor.
- Pilih struktur “Integral” dari grup “Structures”.
- Masukkan batas atas dan bawah integral (jika ada).
- Masukkan fungsi yang akan diintegralkan.
- Tambahkan “dx” untuk menunjukkan variabel integrasi.
- Limit:
- Klik “Equation” untuk membuka Equation Editor.
- Pilih struktur “Limit” dari grup “Structures”.
- Masukkan variabel dan nilai yang didekati.
- Masukkan fungsi yang akan dicari limitnya.
- Matriks:
- Klik “Equation” untuk membuka Equation Editor.
- Pilih struktur “Matriks” dari grup “Structures”.
- Pilih jenis matriks (misalnya, matriks 2×2, 3×3, dll.).
- Masukkan elemen-elemen matriks.
Contoh Penggunaan Rumus Kompleks dalam Soal Matematika
Berikut adalah contoh soal matematika yang menggunakan rumus integral, limit, dan matriks, beserta solusi lengkapnya yang ditulis menggunakan Equation Editor:
- Integral
- Soal Mudah: Hitung ∫(2x + 3) dx dari 0 sampai 1.
Solusi:
∫(2x + 3) dx = [x 2 + 3x] dari 0 sampai 1 = (1 2 + 3*1) – (0 2 + 3*0) = 4
Penjelasan: Soal ini melibatkan integral sederhana dari fungsi linear. - Soal Sedang: Hitung ∫x 2 sin(x) dx.
Solusi: (Penyelesaian menggunakan integrasi parsial, langkah-langkahnya akan terlalu panjang untuk dijelaskan secara detail di sini, namun hasil akhirnya adalah):
∫x 2 sin(x) dx = -x 2 cos(x) + 2x sin(x) + 2 cos(x) + C
Penjelasan: Soal ini memerlukan integrasi parsial. - Soal Sulit: Hitung ∫ 0∞ e -x x n dx (n adalah bilangan bulat positif).
Solusi: (Penyelesaian menggunakan integrasi parsial dan konsep fungsi Gamma, hasil akhirnya adalah):
∫ 0∞ e -x x n dx = n!
Penjelasan: Soal ini melibatkan integral tak wajar dan konsep fungsi Gamma.
- Soal Mudah: Hitung ∫(2x + 3) dx dari 0 sampai 1.
- Limit
- Soal Mudah: Hitung lim x→2 (x 2
4) / (x – 2).
Solusi:
lim x→2 (x 24) / (x – 2) = limx→2 (x – 2)(x + 2) / (x – 2) = lim x→2 (x + 2) = 4
Penjelasan: Soal ini melibatkan limit yang dapat diselesaikan dengan faktorisasi.
- Soal Sedang: Hitung lim x→0 sin(x) / x.
Solusi:
lim x→0 sin(x) / x = 1
Penjelasan: Soal ini adalah limit standar yang sering digunakan dalam kalkulus. - Soal Sulit: Hitung lim x→∞ (1 + 1/x) x.
Solusi:
lim x→∞ (1 + 1/x) x = e
Penjelasan: Soal ini melibatkan limit yang menghasilkan bilangan Euler (e).
- Soal Mudah: Hitung lim x→2 (x 2
- Matriks
- Soal Mudah: Diberikan matriks A = [[1, 2], [3, 4]] dan B = [[5, 6], [7, 8]]. Hitung A + B.
Solusi:
A + B = [[1+5, 2+6], [3+7, 4+8]] = [[6, 8], [10, 12]]
Penjelasan: Soal ini melibatkan penjumlahan matriks sederhana. - Soal Sedang: Diberikan matriks A = [[1, 2], [3, 4]]. Hitung determinan dari A (det(A)).
Solusi:
det(A) = (1*4)
(2*3) = 4 – 6 = -2
Penjelasan: Soal ini melibatkan perhitungan determinan matriks 2×2.
- Soal Sulit: Diberikan matriks A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]. Hitung invers dari A (A -1).
Solusi: (Penyelesaian melibatkan perhitungan determinan, kofaktor, dan adjoin matriks. Hasil akhirnya adalah matriks yang kompleks.)
(Soal ini akan memberikan jawaban yang tidak memiliki invers karena determinan A adalah 0.)
Penjelasan: Soal ini melibatkan perhitungan invers matriks 3×3.
- Soal Mudah: Diberikan matriks A = [[1, 2], [3, 4]] dan B = [[5, 6], [7, 8]]. Hitung A + B.
Latihan Soal Penulisan Rumus Kompleks
Berikut adalah latihan soal untuk menguji kemampuan Anda dalam menulis rumus integral, limit, dan matriks. Solusi dapat diunduh atau ditampilkan di akhir latihan.
- Integral
- Hitung ∫(3x2
2x + 1) dx dari 1 sampai 2.
- Hitung ∫ x cos(x) dx.
- Hitung ∫ 0π/2 sin 2(x) dx.
- Hitung ∫ e x sin(x) dx.
- Hitung ∫ (x 2 + 1) / (x – 1) dx.
Petunjuk: Gunakan Equation Editor untuk menulis rumus dan solusi. Perhatikan penggunaan simbol integral, batas integral, dan dx.
- Hitung ∫(3x2
- Limit
- Hitung limx→1 (x 2
1) / (x – 1).
- Hitung lim x→0 (1 – cos(x)) / x 2.
- Hitung lim x→∞ (2x + 1) / (x – 3).
- Hitung lim x→0 (e x – 1) / x.
- Hitung lim x→π/2 tan(x).
Petunjuk: Gunakan Equation Editor untuk menulis rumus dan solusi. Perhatikan penggunaan simbol limit, variabel yang mendekati, dan fungsi.
- Hitung limx→1 (x 2
- Matriks
- Diberikan matriks A = [[2, 1], [0, 3]] dan B = [[-1, 2], [1, -2]]. Hitung 2A – B.
- Diberikan matriks A = [[1, 2], [3, 4]]. Hitung A
A (A kuadrat).
- Diberikan matriks A = [[1, 0, 2], [-1, 3, 1], [0, 1, 0]]. Hitung determinan A.
- Diberikan matriks A = [[1, 2], [3, 4]]. Hitung invers A.
- Diberikan matriks A = [[1, 2], [3, 4]] dan B = [[5, 6], [7, 8]]. Hitung A – B.
Petunjuk: Gunakan Equation Editor untuk menulis rumus dan solusi. Perhatikan penggunaan struktur matriks, elemen matriks, dan operasi matriks.
Solusi Latihan Soal: (Solusi akan ditampilkan di sini setelah selesai mengerjakan latihan.)
(Catatan: Karena keterbatasan format, solusi soal latihan tidak dapat ditampilkan secara langsung di sini. Solusi akan berupa file terpisah yang dapat diunduh atau ditampilkan.)
Contoh Penulisan Integral dan Limit
Contoh Penulisan Integral:
Rumus: ∫(x 2 + 2x + 1) dx
Penjelasan:
- Simbol integral (∫) dapat ditemukan di Equation Editor.
- Gunakan superscript (^) untuk pangkat.
- Gunakan simbol ‘dx’ untuk menunjukkan variabel integrasi.
Contoh Penulisan Limit:
Rumus: lim (x→2) (x 2
-4) / (x – 2)Penjelasan:
- Gunakan ‘lim’ untuk limit, yang dapat ditemukan di Equation Editor.
- Gunakan panah (→) untuk menunjukkan pendekatan.
- Gunakan fraksi untuk menulis pecahan.
Panduan Penggunaan Matriks
Membuat dan mengolah matriks di Word sangat mudah dengan Equation Editor. Berikut adalah langkah-langkah dan tipsnya:
- Membuat Matriks:
- Buka Equation Editor.
- Klik “Matrix” di grup “Structures”.
- Pilih jenis matriks yang diinginkan (2×2, 3×3, dll.).
- Word akan menampilkan struktur matriks dengan kotak-kotak kosong untuk diisi.
- Untuk matriks dengan ukuran yang tidak tersedia, Anda dapat memilih matriks dengan ukuran terdekat, lalu menambahkan atau menghapus baris dan kolom menggunakan tombol “Insert” atau “Delete” pada grup “Structures”.
- Memasukkan Elemen Matriks:
- Klik pada kotak di dalam struktur matriks.
- Ketikkan angka atau variabel yang sesuai.
- Gunakan tombol panah atau klik untuk berpindah antar elemen.
- Operasi Matematika pada Matriks:
- Penjumlahan dan Pengurangan: Gunakan simbol “+” dan “-” di antara matriks.
- Perkalian Skalar: Kalikan matriks dengan angka (skalar).
- Perkalian Matriks: Gunakan simbol “·” (dot product) atau ketik langsung. Pastikan ukuran matriks sesuai untuk perkalian.
Contoh Soal Operasi Matriks dan Solusi:
Diberikan matriks A = [[1, 2], [3, 4]] dan B = [[5, 6], [7, 8]]. Hitung A
– B.
Solusi:
A
– B = [[(1*5 + 2*7), (1*6 + 2*8)], [(3*5 + 4*7), (3*6 + 4*8)]] = [[19, 22], [43, 50]]
Oke, mari kita mulai dengan rumus matematika di Word. Tapi, pernahkah Anda berpikir bagaimana cara memindahkan file penting dari ponsel ke komputer untuk mengerjakan soal-soal? Nah, sebelum kita lanjut, pastikan Anda sudah tahu cara memindah file dari hp ke komputer dengan kabel data , karena itu bisa sangat membantu saat Anda perlu menyalin contoh soal. Setelah file soal matematika ada di komputer, barulah kita bisa mulai menulis rumus-rumus rumit dengan mudah di Word.
Penjelasan: Soal ini melibatkan perkalian matriks. Setiap elemen pada matriks hasil diperoleh dengan mengalikan elemen baris matriks pertama dengan elemen kolom matriks kedua, lalu menjumlahkannya.
Latihan Soal Operasi Matriks: (Sudah ada di bagian Latihan Soal sebelumnya)
Tips untuk Penulisan Rumus yang Lebih Efisien
Untuk meningkatkan efisiensi penulisan rumus di Word, berikut beberapa tips yang dapat Anda terapkan:
- Gunakan Simbol Matematika yang Umum:
- Pelajari dan gunakan simbol-simbol matematika yang umum (misalnya, π, ∞, ∑, ∫). Simbol-simbol ini dapat ditemukan di grup “Symbols” pada tab “Design” di Equation Editor.
- Gunakan karakter Unicode untuk simbol-simbol yang tidak tersedia secara langsung di Equation Editor.
- Atur Rumus agar Mudah Dibaca:
- Gunakan spasi yang cukup antar simbol dan angka.
- Gunakan kurung untuk mengelompokkan ekspresi.
- Gunakan pecahan, akar, dan pangkat secara tepat.
- Manfaatkan Shortcut Keyboard: (Sudah dijelaskan sebelumnya)
- Simpan Rumus sebagai Objek yang Dapat Digunakan Kembali:
- Setelah menulis rumus, pilih rumus tersebut.
- Klik tab “Insert”.
- Klik “Quick Parts” di grup “Text”.
- Pilih “Save Selection to Quick Part Gallery…”.
- Berikan nama untuk rumus dan simpan.
- Untuk menggunakan kembali rumus, ketik nama rumus, lalu tekan F3.
Menggunakan Fitur AutoCorrect untuk Rumus
Fitur AutoCorrect di Microsoft Word adalah alat yang sangat berguna, seringkali diremehkan, untuk mempercepat dan mempermudah penulisan rumus matematika. Fitur ini memungkinkan pengguna untuk membuat singkatan khusus yang secara otomatis akan digantikan dengan simbol, rumus, atau ekspresi matematika yang lebih panjang. Ini tidak hanya menghemat waktu tetapi juga mengurangi risiko kesalahan pengetikan, terutama ketika berhadapan dengan simbol-simbol kompleks dan rumus yang sering digunakan.
AutoCorrect mengatasi kelemahan penulisan rumus manual dengan menyediakan cara cepat dan konsisten untuk memasukkan elemen matematika. Daripada mengetik simbol atau rumus panjang berulang kali, pengguna dapat membuat singkatan yang mudah diingat. Saat singkatan ini diketik, Word secara otomatis menggantinya dengan entri AutoCorrect yang telah ditentukan sebelumnya. Ini sangat bermanfaat dalam situasi di mana waktu adalah faktor penting, seperti saat mengerjakan tugas atau ujian, atau ketika menulis dokumen yang memerlukan banyak rumus matematika.
Peran AutoCorrect
Fitur AutoCorrect dalam Microsoft Word memainkan peran penting dalam menyederhanakan penulisan rumus matematika. Dengan memanfaatkan fitur ini, pengguna dapat mempercepat penulisan berbagai jenis rumus, mulai dari aljabar dasar hingga kalkulus yang kompleks, trigonometri, dan statistik. AutoCorrect tidak hanya mempercepat proses penulisan, tetapi juga mengurangi kemungkinan kesalahan pengetikan yang sering terjadi saat memasukkan simbol dan rumus matematika secara manual.
AutoCorrect mengatasi kelemahan penulisan rumus manual dengan menyediakan mekanisme otomatis untuk menggantikan singkatan yang telah ditentukan sebelumnya dengan simbol atau rumus yang lebih panjang. Misalnya, pengguna dapat menetapkan singkatan “a” untuk simbol alfa (α) atau “int” untuk simbol integral (∫). Ketika singkatan-singkatan ini diketik dalam dokumen, Word secara otomatis menggantinya dengan simbol atau rumus yang sesuai. Hal ini sangat berguna dalam mengatasi kesulitan dalam mengingat kode Unicode atau mencari simbol matematika di menu simbol setiap saat.
Contoh Pengaturan AutoCorrect
Berikut adalah tabel contoh pengaturan AutoCorrect yang sangat berguna untuk penulisan rumus matematika:
| Simbol/Rumus | Singkatan | Deskripsi |
|---|---|---|
| α | a | Simbol alfa (huruf Yunani) |
| ∫ | int | Simbol integral |
| ∑ | sum | Simbol penjumlahan (sigma) |
| √(x) | sqrtx | Akar kuadrat dari x |
| β | b | Simbol beta (huruf Yunani) |
| θ | th | Simbol theta (huruf Yunani) |
| ∞ | inf | Simbol tak hingga |
| ± | pm | Simbol plus-minus |
| ≠ | ne | Simbol tidak sama dengan |
| ≈ | ap | Simbol hampir sama dengan |
Pengaturan AutoCorrect harus mempertimbangkan variasi dalam penulisan rumus. Contohnya, pengguna dapat mengatur AutoCorrect untuk mengenali huruf besar dan kecil. Singkatan “a” dapat menggantikan simbol alfa (α), sementara “A” dapat menggantikan simbol yang berbeda atau versi huruf besar dari simbol alfa (Α). Penggunaan spasi juga penting; AutoCorrect dapat diatur untuk memasukkan spasi secara otomatis di sekitar operator matematika (misalnya, “x+y” menjadi “x + y”).
Daftar Singkatan yang Direkomendasikan
Berikut adalah daftar singkatan yang direkomendasikan untuk mempercepat penulisan simbol matematika, operator, dan rumus:
- Simbol Yunani:
- a: α (alfa)
- b: β (beta)
- g: γ (gamma)
- d: δ (delta)
- th: θ (theta)
- l: λ (lambda)
- o: ω (omega)
- Operator Matematika:
- pm: ± (plus-minus)
- mp: ∓ (minus-plus)
- ne: ≠ (tidak sama dengan)
- le: ≤ (kurang dari atau sama dengan)
- ge: ≥ (lebih dari atau sama dengan)
- inf: ∞ (tak hingga)
- div: ÷ (pembagian)
- cdot: ⋅ (titik tengah)
- Fungsi Trigonometri:
- sin: sin(x)
- cos: cos(x)
- tan: tan(x)
- csc: csc(x)
- sec: sec(x)
- cot: cot(x)
- Limit, Turunan, dan Integral:
- lim: lim (limit)
- der: d/dx (turunan)
- int: ∫ (integral)
- iint: ∬ (integral ganda)
- iiint: ∭ (integral rangkap tiga)
- Rumus yang Umum Digunakan:
- kuadrat: x²
- pyth: a² + b² = c² (teorema Pythagoras)
- rata: x̄ (rata-rata)
- sd: σ (standar deviasi)
Langkah-Langkah Membuat dan Mengelola Entri AutoCorrect
Berikut adalah panduan langkah-demi-langkah untuk membuat, mengedit, menghapus, dan mengelola entri AutoCorrect dalam Microsoft Word:
- Buka Opsi AutoCorrect: Buka dokumen Word baru atau yang sudah ada. Klik pada “File” di sudut kiri atas, kemudian pilih “Opsi”. Di jendela “Opsi Word”, pilih “Pembuktian” dari menu di sebelah kiri. Di bagian “Opsi Koreksi Otomatis”, klik tombol “Opsi Koreksi Otomatis…”.
- Membuat Entri Baru: Di jendela “Koreksi Otomatis”, pada tab “Koreksi Otomatis”, ketik singkatan yang ingin Anda gunakan di kotak “Ganti”. Di kotak “Dengan”, ketik simbol atau rumus yang ingin Anda masukkan. Misalnya, ketik “a” di kotak “Ganti” dan “α” di kotak “Dengan”. Klik “Tambahkan”, lalu klik “OK” untuk menyimpan entri.
- Mengedit Entri: Untuk mengedit entri yang sudah ada, pilih entri tersebut dari daftar. Ubah singkatan atau simbol/rumus di kotak “Ganti” atau “Dengan”. Klik “Ganti”, lalu klik “OK” untuk menyimpan perubahan.
- Menghapus Entri: Pilih entri yang ingin Anda hapus dari daftar. Klik “Hapus”, lalu klik “OK” untuk menghapus entri.
- Mengelola Pengecualian: Pada tab “Kecualikan”, Anda dapat menentukan pengecualian untuk AutoCorrect. Misalnya, Anda dapat mencegah AutoCorrect mengganti singkatan tertentu dalam situasi tertentu.
- Pengaturan Tambahan: Periksa opsi yang tersedia di jendela “Koreksi Otomatis”. Pastikan opsi seperti “Ganti teks saat Anda mengetik” dicentang agar AutoCorrect berfungsi.
Berikut adalah screenshot dari antarmuka AutoCorrect di Word:
Ilustrasi: Screenshot dari jendela “Koreksi Otomatis” di Microsoft Word. Jendela tersebut menampilkan tab “Koreksi Otomatis” dengan kotak “Ganti” dan “Dengan”, serta daftar entri AutoCorrect yang ada. Terdapat tombol “Tambahkan”, “Ganti”, dan “Hapus”.
Tips dan Trik:
- Gunakan Karakter Khusus: Gunakan kode Unicode atau sisipkan simbol matematika langsung untuk memastikan representasi yang benar.
- Perhatikan Spasi: Pastikan ada spasi yang tepat di sekitar operator dan simbol untuk keterbacaan.
- Hindari Konflik: Pilih singkatan yang unik dan tidak mungkin berbenturan dengan kata-kata umum.
- Uji Coba: Selalu uji entri AutoCorrect setelah dibuat untuk memastikan berfungsi seperti yang diharapkan.
Penanganan Kasus Khusus
AutoCorrect menangani kasus khusus seperti penulisan indeks dan pangkat dalam rumus dengan cara yang berbeda. Misalnya, pengguna dapat membuat singkatan seperti “x2” untuk menghasilkan “x²”. Word secara otomatis akan mengenali karakter angka setelah huruf dan memformatnya sebagai pangkat. Demikian pula, untuk indeks, pengguna dapat membuat singkatan seperti “x_1” untuk menghasilkan “x₁”.
AutoCorrect dapat digunakan untuk menyisipkan simbol matematika yang kompleks. Misalnya, pengguna dapat membuat entri untuk matriks. Pengguna dapat membuat singkatan seperti “mat2x2” yang akan menggantikan singkatan dengan template matriks 2×2, dengan placeholder yang memungkinkan pengguna memasukkan nilai-nilai yang sesuai.
Contoh:
- Pangkat: Jika pengguna mengetik “x2”, AutoCorrect dapat mengubahnya menjadi “x²”.
- Indeks: Jika pengguna mengetik “a_i”, AutoCorrect dapat mengubahnya menjadi “aᵢ”.
- Matriks: Jika pengguna mengetik “mat2x2”, AutoCorrect dapat menyisipkan template matriks 2×2.
Uji Coba
Setelah membuat entri AutoCorrect, penting untuk mengujinya untuk memastikan berfungsi dengan benar. Berikut adalah contoh uji coba:
- Uji Coba untuk Simbol Yunani: Ketik singkatan “a” (tanpa tanda kutip) dan pastikan digantikan dengan simbol alfa (α).
- Uji Coba untuk Integral: Ketik singkatan “int” (tanpa tanda kutip) dan pastikan digantikan dengan simbol integral (∫).
- Uji Coba untuk Rumus Kuadrat: Ketik singkatan “kuadrat” (tanpa tanda kutip) dan pastikan digantikan dengan x².
- Uji Coba untuk Teorema Pythagoras: Ketik singkatan “pyth” (tanpa tanda kutip) dan pastikan digantikan dengan a² + b² = c².
Jika uji coba ini berhasil, berarti entri AutoCorrect telah dibuat dengan benar dan siap digunakan dalam penulisan rumus matematika.
Penulisan
Menggunakan AutoCorrect dalam penulisan rumus matematika menawarkan sejumlah manfaat signifikan. Fitur ini meningkatkan produktivitas dengan memungkinkan pengguna untuk dengan cepat memasukkan simbol dan rumus kompleks tanpa harus mencari atau mengetiknya berulang kali. Penggunaan AutoCorrect juga mengurangi kesalahan pengetikan, memastikan konsistensi dalam dokumen, dan menghemat waktu berharga. Dengan memanfaatkan fitur ini, pengguna dapat meningkatkan efisiensi penulisan rumus matematika, menghasilkan dokumen yang lebih akurat dan profesional.
Menyisipkan Rumus dari Aplikasi Lain
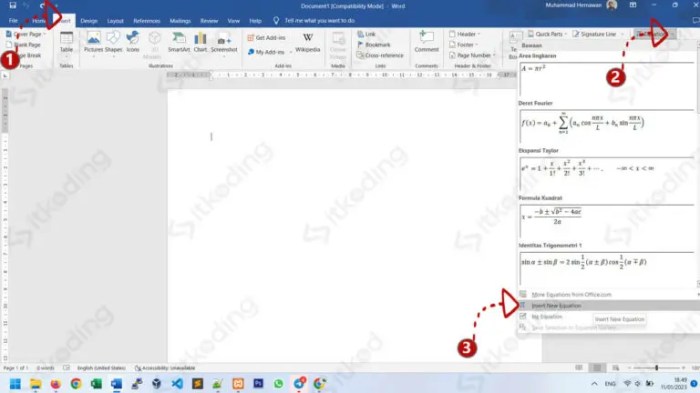
Source: itkoding.com
Kemampuan untuk menyisipkan rumus matematika dari aplikasi lain ke dalam Microsoft Word sangat penting bagi para penulis, peneliti, dan mahasiswa. Hal ini memungkinkan penggunaan alat khusus seperti LaTeX atau MathType, yang menawarkan fleksibilitas dan kekuatan lebih dalam penulisan rumus kompleks. Artikel ini akan membahas secara mendalam berbagai metode, tips, contoh kasus, dan demonstrasi langkah demi langkah untuk mencapai hal ini.
Penyisipan rumus yang efektif dari aplikasi lain ke Word memerlukan pemahaman tentang berbagai teknik dan pertimbangan untuk memastikan kualitas dan kompatibilitas yang optimal.
Perincian Teknis Penyisipan
Terdapat beberapa metode utama untuk menyisipkan rumus dari aplikasi lain ke dalam Microsoft Word. Setiap metode memiliki kelebihan dan kekurangan, tergantung pada kebutuhan pengguna.
- Menyisipkan sebagai Objek: Metode ini melibatkan penyisipan rumus sebagai objek yang tertanam. Word akan menyimpan rumus tersebut dalam format yang dikenali oleh aplikasi asalnya (misalnya, MathType atau LaTeX). Keuntungannya adalah rumus dapat diedit kembali di aplikasi asalnya. Kekurangannya adalah ukuran file bisa bertambah besar, dan tampilan mungkin berubah jika aplikasi asalnya tidak tersedia di komputer lain.
- Menyisipkan sebagai Gambar: Rumus dapat diekspor dari aplikasi lain sebagai gambar (misalnya, PNG, JPG, atau EPS) dan kemudian disisipkan ke dalam Word. Metode ini sederhana dan memastikan tampilan yang konsisten di berbagai komputer. Namun, rumus tidak dapat diedit langsung di Word, dan kualitas gambar dapat menurun jika ukurannya diubah.
- Menggunakan OLE (Object Linking and Embedding): OLE memungkinkan rumus ditautkan ke aplikasi asalnya. Perubahan pada rumus di aplikasi asalnya akan secara otomatis diperbarui di Word. Ini berguna untuk dokumen yang sering diperbarui. Namun, pengguna harus memiliki aplikasi asalnya terinstal di komputer mereka untuk melihat dan mengedit rumus.
Word mendukung berbagai format file untuk penyisipan rumus, termasuk:
- EPS (Encapsulated PostScript): Format ini sering digunakan untuk menyimpan grafik vektor dan umumnya didukung oleh aplikasi seperti LaTeX.
- PDF (Portable Document Format): PDF dapat menyimpan rumus sebagai gambar atau vektor. Word dapat mengimpor file PDF, tetapi kualitasnya bervariasi.
- DOCX (Microsoft Word Document): Dalam beberapa kasus, rumus yang dibuat di aplikasi lain dapat disisipkan langsung ke dalam dokumen DOCX. Ini tergantung pada kompatibilitas antara aplikasi dan versi Word.
Tips untuk Mempertahankan Kualitas Rumus
Memastikan kualitas rumus yang disisipkan adalah kunci untuk dokumen yang profesional dan mudah dibaca. Berikut adalah beberapa tips untuk mencapai hal tersebut.
- Resolusi: Saat menyisipkan sebagai gambar, pastikan resolusi gambar cukup tinggi untuk menghindari tampilan buram. Gunakan resolusi yang sesuai dengan ukuran rumus dalam dokumen.
- Ukuran dan Skala: Atur ukuran dan skala rumus yang disisipkan agar sesuai dengan dokumen Word. Hindari mengubah ukuran gambar secara berlebihan, karena dapat mengurangi kualitasnya.
- Keterbacaan: Pilih font dan ukuran yang mudah dibaca. Pastikan rumus memiliki kontras yang cukup dengan latar belakang.
- Tampilan di Berbagai Komputer: Jika menggunakan objek tertanam atau OLE, pastikan aplikasi asalnya tersedia di komputer lain. Jika tidak, gunakan format gambar atau PDF untuk tampilan yang konsisten.
Berikut adalah beberapa solusi untuk masalah umum:
- Rumus Buram: Periksa resolusi gambar atau gunakan format vektor seperti EPS.
- Perubahan Tampilan: Gunakan format yang didukung oleh semua versi Word atau pastikan aplikasi asalnya terinstal.
- Ukuran File Besar: Optimalkan gambar atau gunakan format yang lebih efisien.
Tabel berikut membandingkan kelebihan dan kekurangan berbagai metode penyisipan:
| Metode | Kualitas | Ukuran File | Kemudahan Pengeditan | Kompatibilitas |
|---|---|---|---|---|
| Objek (MathType, dll.) | Tinggi (dapat diedit) | Cukup besar | Tinggi (dengan aplikasi asal) | Tergantung aplikasi asal |
| Gambar (PNG, JPG, EPS) | Tergantung resolusi | Kecil hingga sedang | Rendah (tidak dapat diedit langsung) | Tinggi |
| OLE | Tinggi (dapat diedit) | Cukup besar | Tinggi (dengan aplikasi asal) | Membutuhkan aplikasi asal terinstal |
Contoh Kasus Penggunaan
Penyisipan rumus dari aplikasi lain sangat bermanfaat dalam berbagai konteks. Berikut adalah tiga contoh kasus penggunaan nyata.
- Penulisan Makalah Ilmiah: Peneliti sering menggunakan LaTeX untuk menulis makalah ilmiah karena kemampuannya yang kuat dalam menangani rumus kompleks.
- Aplikasi: LaTeX
- Jenis Rumus: Persamaan matematika, integral, limit, matriks.
- Manfaat: Kemudahan dalam menulis rumus kompleks, tampilan yang konsisten, dan kemampuan untuk mengelola struktur dokumen.
- Contoh Tampilan Akhir: Persamaan matematika yang rumit dengan simbol dan notasi standar ilmiah.
- Pembuatan Laporan Teknis: Insinyur dan ilmuwan sering menggunakan MathType untuk membuat laporan teknis yang berisi rumus dan diagram.
- Aplikasi: MathType
- Jenis Rumus: Rumus fisika, kimia, dan teknik.
- Manfaat: Antarmuka yang mudah digunakan, berbagai simbol matematika, dan integrasi dengan Word.
- Contoh Tampilan Akhir: Diagram rangkaian listrik dengan persamaan dan notasi yang jelas.
- Pembuatan Soal Ujian Matematika: Guru matematika sering menggunakan aplikasi seperti LaTeX atau MathType untuk membuat soal ujian yang berisi rumus dan grafik.
- Aplikasi: LaTeX atau MathType
- Jenis Rumus: Persamaan aljabar, kalkulus, dan geometri.
- Manfaat: Kemampuan untuk membuat soal yang kompleks dan memastikan tampilan yang konsisten.
- Contoh Tampilan Akhir: Soal ujian matematika dengan rumus dan grafik yang jelas dan mudah dibaca.
Demonstrasi Langkah demi Langkah (LaTeX ke Word), Cara menulis rumus mtk di word
Berikut adalah demonstrasi langkah demi langkah tentang cara menyisipkan rumus dari LaTeX ke Word menggunakan metode yang direkomendasikan.
- Menulis Rumus di LaTeX: Gunakan paket `amsmath` dan `graphicx` dalam LaTeX. Contoh kode LaTeX:
- Mengonversi ke Format yang Kompatibel: Konversi kode LaTeX menjadi gambar (PNG, JPG, atau EPS) menggunakan editor LaTeX (misalnya, TeXstudio) atau konverter online.
- Menyisipkan Gambar ke Word: Di Word, pilih “Insert” > “Pictures” dan pilih file gambar yang dihasilkan.
- Mengatur Ukuran dan Posisi: Atur ukuran dan posisi gambar agar sesuai dengan dokumen.
- Mengedit (Opsional): Jika perlu, edit rumus di LaTeX dan ulangi langkah konversi dan penyisipan.
\documentclassarticle
\usepackageamsmath
\usepackagegraphicx
\begindocument
\beginequation
E = mc^2
\endequation
\enddocument
Visualisasi langkah-langkah:
- Langkah 1: Tampilan kode LaTeX di editor (TeXstudio).
- Langkah 2: Tampilan hasil konversi LaTeX menjadi gambar (misalnya, PNG)
- Langkah 3: Tampilan rumus yang sudah disisipkan di Word.
Peringatan: Pastikan kompatibilitas antara versi LaTeX, konverter, dan Word. Beberapa konverter mungkin memerlukan pengaturan khusus. Perhatikan bahwa konversi langsung dari LaTeX ke Word (misalnya, menggunakan add-in) mungkin tidak selalu menghasilkan hasil yang optimal. Gunakan format gambar sebagai alternatif jika terjadi masalah.
Format dan Tata Letak Rumus
Membuat rumus matematika di Microsoft Word lebih dari sekadar mengetik simbol; ini tentang menyajikan informasi secara jelas dan profesional. Format dan tata letak yang baik sangat penting untuk memastikan rumus mudah dipahami, terutama dalam dokumen ilmiah, laporan, atau presentasi. Dengan memperhatikan detail-detail ini, Anda dapat meningkatkan kualitas dokumen secara keseluruhan dan memastikan pesan matematika tersampaikan dengan efektif.
Mari kita telusuri bagaimana mengatur format dan tata letak rumus matematika di Word agar terlihat optimal.
Mengatur Format dan Tata Letak Rumus yang Profesional
Menyajikan rumus matematika dengan format yang tepat meningkatkan keterbacaan dan profesionalisme dokumen. Berikut adalah beberapa aspek penting yang perlu diperhatikan:
- Konsistensi: Pastikan semua rumus menggunakan format yang sama, termasuk ukuran font, jenis font, dan spasi. Gunakan gaya (styles) yang tersedia di Word untuk menerapkan format yang seragam.
- Ukuran Font: Gunakan ukuran font yang cukup besar agar mudah dibaca. Pertimbangkan ukuran font yang sedikit lebih besar dari teks biasa dalam dokumen.
- Spasi: Berikan spasi yang cukup di sekitar operator matematika (+, -, =, dll.) dan di antara elemen-elemen dalam rumus. Hindari kerumunan elemen yang membuat rumus sulit dibaca.
- Penjajaran: Sejajarkan persamaan atau rumus yang berurutan secara vertikal untuk memudahkan perbandingan. Gunakan fitur tab atau tabel untuk mengatur penjajaran.
- Gunakan Kurung: Gunakan kurung, tanda kurung siku, dan kurung kurawal dengan tepat untuk mengelompokkan elemen-elemen dalam rumus. Pastikan kurung cukup besar untuk menampung semua elemen di dalamnya.
Tips Memastikan Konsistensi Format Rumus dalam Dokumen
Konsistensi adalah kunci untuk dokumen yang profesional. Berikut adalah beberapa tips untuk memastikan format rumus tetap konsisten:
- Gunakan Gaya (Styles): Word menyediakan gaya (styles) untuk rumus. Gunakan gaya ini untuk menerapkan format yang seragam ke semua rumus. Anda dapat memodifikasi gaya untuk menyesuaikan tampilan.
- Buat Templat: Buat templat dokumen yang sudah berisi gaya format rumus yang diinginkan. Ini akan memastikan bahwa semua dokumen baru menggunakan format yang sama.
- Periksa Secara Berkala: Periksa kembali dokumen secara berkala untuk memastikan semua rumus diformat dengan benar. Gunakan fitur “Find and Replace” untuk menemukan dan memperbaiki inkonsistensi.
- Gunakan Editor Persamaan: Manfaatkan fitur Editor Persamaan di Word. Editor ini menyediakan alat untuk membuat rumus dengan format yang konsisten.
Contoh Format Rumus yang Baik dan Buruk
Mari kita lihat beberapa contoh untuk membedakan format yang baik dan buruk.
Contoh Format Buruk:
x+y=5
a/b+c=2
(2+3)*4
Penjelasan: Contoh di atas memiliki spasi yang tidak konsisten, ukuran font yang mungkin berbeda, dan kurangnya penggunaan kurung yang tepat. Ini membuat rumus sulit dibaca dan kurang profesional.
Contoh Format Baik:
Oke, mari kita mulai dengan rumus matematika di Word. Tapi, pernahkah Anda berpikir bagaimana cara memindahkan file penting dari ponsel ke komputer untuk mengerjakan soal-soal? Nah, sebelum kita lanjut, pastikan Anda sudah tahu cara memindah file dari hp ke komputer dengan kabel data , karena itu bisa sangat membantu saat Anda perlu menyalin contoh soal. Setelah file soal matematika ada di komputer, barulah kita bisa mulai menulis rumus-rumus rumit dengan mudah di Word.
x + y = 5
\(\fracab + c = 2\)
(2 + 3) – 4
Penjelasan: Contoh di atas menggunakan spasi yang konsisten, ukuran font yang sesuai, dan kurung yang tepat. Rumus lebih mudah dibaca dan terlihat profesional.
Demonstrasi Langkah demi Langkah Mengatur Format Rumus di Word
Berikut adalah langkah-langkah untuk mengatur format rumus di Microsoft Word:
- Buka Editor Persamaan: Klik “Insert” > “Equation” untuk membuka editor persamaan.
- Masukkan Rumus: Ketik rumus menggunakan simbol dan template yang tersedia di editor.
- Pilih Font dan Ukuran: Pilih font dan ukuran font yang sesuai untuk rumus.
- Atur Spasi: Tambahkan spasi di sekitar operator matematika dan elemen-elemen rumus.
- Gunakan Kurung: Gunakan kurung, tanda kurung siku, dan kurung kurawal dengan tepat.
- Sejajarkan Persamaan: Jika memiliki beberapa persamaan, sejajarkan secara vertikal.
- Gunakan Gaya (Styles): Jika perlu, terapkan gaya untuk konsistensi format.
- Simpan: Simpan dokumen.
Troubleshooting
Menulis rumus matematika di Microsoft Word, meskipun didukung fitur canggih, tidak selalu berjalan mulus. Seringkali pengguna menemui kendala yang menghambat proses pengetikan dan penyuntingan rumus. Bagian ini akan mengidentifikasi masalah umum, memberikan solusi praktis, dan menyajikan daftar pertanyaan yang sering diajukan untuk membantu pengguna mengatasi kesulitan tersebut.
Bagi Anda yang sering berurusan dengan angka dan simbol matematika, tentu tahu betapa pentingnya bisa menulis rumus dengan rapi di Word. Namun, pernahkah Anda merasa bahwa ada hal lain yang tak kalah penting, seperti kewajiban agama? Sama halnya dengan kesulitan menulis rumus, mengganti shalat yang terlewatkan juga memerlukan perencanaan dan kedisiplinan, lebih detailnya bisa Anda temukan di cara mengganti shalat yang terlewatkan.
Setelah selesai menunaikan kewajiban, kembali lagi ke Word, karena kemampuan menulis rumus yang baik akan sangat membantu dalam pekerjaan atau studi Anda.
Tujuan utama dari bagian ini adalah untuk memberikan pemahaman yang komprehensif tentang masalah yang mungkin timbul dan bagaimana cara mengatasinya, sehingga pengguna dapat menulis rumus matematika dengan lebih efisien dan efektif.
Identifikasi Masalah Umum
Beberapa masalah umum seringkali menghambat produktivitas saat menulis rumus matematika di Word. Pemahaman terhadap masalah-masalah ini adalah langkah awal untuk menemukan solusi yang tepat.
- Rumus Tidak Muncul atau Hilang: Rumus yang sudah diketik tiba-tiba hilang atau tidak muncul saat dokumen disimpan atau dibuka kembali.
- Simbol Tidak Tampil dengan Benar: Simbol matematika tertentu, seperti integral atau simbol khusus lainnya, ditampilkan dalam format yang salah atau bahkan tidak muncul sama sekali.
- Kesulitan dalam Mengedit Rumus: Proses pengeditan rumus terasa sulit, terutama ketika melibatkan struktur yang kompleks seperti matriks atau persamaan multi-baris.
- Format Rumus yang Berantakan: Spasi, ukuran huruf, atau penempatan simbol tidak sesuai dengan yang diinginkan, sehingga rumus terlihat tidak rapi.
- Error Saat Menggunakan Persamaan: Muncul pesan kesalahan atau error saat mencoba memasukkan atau mengedit persamaan, seringkali berkaitan dengan sintaks atau format yang tidak tepat.
Solusi untuk Setiap Masalah
Setelah mengidentifikasi masalah umum, langkah selanjutnya adalah mencari solusi yang tepat. Berikut adalah beberapa solusi yang dapat diterapkan untuk mengatasi masalah-masalah tersebut:
- Rumus Tidak Muncul atau Hilang:
- Periksa Pengaturan Tampilan: Pastikan opsi “Show Equations” atau “Tampilkan Persamaan” diatur dalam pengaturan Word. Terkadang, pengaturan ini dapat dinonaktifkan secara tidak sengaja.
- Perbarui Word: Pastikan versi Microsoft Word yang digunakan adalah versi terbaru untuk menghindari bug yang mungkin menyebabkan masalah tampilan.
- Perbaiki File: Jika masalah berlanjut, coba perbaiki file dokumen melalui fitur “Open and Repair” yang ada di Word.
- Simbol Tidak Tampil dengan Benar:
- Gunakan Font yang Tepat: Pastikan font yang digunakan mendukung simbol matematika yang diperlukan. Font seperti Cambria Math atau Symbol biasanya menyediakan berbagai simbol matematika.
- Periksa Kode Simbol: Jika simbol tertentu masih tidak muncul, periksa kode Unicode atau kode karakter simbol tersebut dan masukkan secara manual.
- Sisipkan Simbol: Gunakan fitur “Insert Symbol” atau “Sisipkan Simbol” yang ada di Word untuk memilih dan menyisipkan simbol yang benar.
- Kesulitan dalam Mengedit Rumus:
- Gunakan Editor Persamaan: Manfaatkan editor persamaan bawaan Word untuk mengedit rumus dengan lebih mudah. Editor ini menyediakan berbagai alat dan fitur untuk membantu.
- Gunakan Struktur yang Tepat: Gunakan template atau struktur yang sesuai (misalnya, matriks, pecahan, integral) untuk mempermudah pengeditan rumus kompleks.
- Gunakan Keyboard Shortcuts: Pelajari dan gunakan pintasan keyboard ( keyboard shortcuts) untuk mempercepat proses pengeditan, seperti Ctrl+Z untuk membatalkan atau Ctrl+Y untuk mengulangi.
- Format Rumus yang Berantakan:
- Gunakan Style: Terapkan gaya ( style) yang telah ditentukan untuk rumus matematika untuk memastikan konsistensi format.
- Sesuaikan Spasi: Gunakan opsi pengaturan spasi dalam editor persamaan untuk mengontrol jarak antara simbol, angka, dan operator.
- Periksa Ukuran Huruf: Pastikan ukuran huruf konsisten dan sesuai dengan kebutuhan.
- Error Saat Menggunakan Persamaan:
- Periksa Sintaks: Pastikan sintaks atau tata bahasa rumus yang digunakan benar.
- Gunakan Tanda Kurung dengan Tepat: Pastikan penggunaan tanda kurung (kurung biasa, kurung siku, kurung kurawal) sesuai dengan urutan operasi matematika.
- Perbaiki Persamaan: Jika kesalahan masih terjadi, coba perbaiki persamaan dengan mengulangi proses pengetikan atau menggunakan fitur perbaikan otomatis yang tersedia di Word.
Pertanyaan Umum (FAQ)
Berikut adalah beberapa pertanyaan umum (FAQ) yang sering diajukan terkait penulisan rumus matematika di Word, beserta jawabannya:
- Bagaimana cara menyisipkan rumus matematika di Word?
Buka tab “Insert” atau “Sisipkan”, kemudian klik “Equation” atau “Persamaan”. Anda dapat memilih dari beberapa rumus yang telah ditentukan atau mulai mengetik rumus baru.
- Mengapa simbol matematika saya tidak muncul dengan benar?
Kemungkinan besar, Anda menggunakan font yang tidak mendukung simbol matematika yang dibutuhkan. Pastikan Anda menggunakan font seperti Cambria Math atau Symbol.
- Bagaimana cara membuat pecahan di Word?
Di editor persamaan, gunakan template pecahan yang tersedia atau ketikkan simbol garis miring (/) untuk membuat pecahan. Word akan secara otomatis mengubahnya menjadi format pecahan yang benar.
- Apakah ada pintasan keyboard untuk menulis rumus matematika?
Ya, ada. Beberapa contohnya adalah Ctrl+= untuk memulai pengetikan rumus, dan Anda juga dapat menggunakan pintasan untuk simbol-simbol tertentu.
- Bagaimana cara memperbaiki rumus yang rusak atau tidak muncul?
Periksa pengaturan tampilan, perbarui Word, atau perbaiki file dokumen. Jika masalah berlanjut, periksa sintaks dan format rumus yang digunakan.
Daftar Masalah, Penyebab, dan Solusi
Tabel berikut merangkum masalah umum, penyebabnya, dan solusi yang dapat diterapkan untuk mengatasi masalah tersebut.
| Masalah | Penyebab | Solusi |
|---|---|---|
| Rumus Tidak Muncul atau Hilang | Pengaturan tampilan dinonaktifkan, versi Word usang, kerusakan file. | Periksa pengaturan tampilan, perbarui Word, perbaiki file. |
| Simbol Tidak Tampil dengan Benar | Font yang digunakan tidak mendukung simbol, kode simbol salah. | Gunakan font yang tepat (Cambria Math), periksa kode simbol, gunakan “Insert Symbol”. |
| Kesulitan dalam Mengedit Rumus | Penggunaan editor persamaan yang kurang optimal, struktur rumus yang kompleks. | Gunakan editor persamaan, gunakan struktur yang tepat, gunakan pintasan keyboard. |
| Format Rumus yang Berantakan | Tidak menggunakan style, pengaturan spasi yang salah. | Gunakan style, sesuaikan spasi, periksa ukuran huruf. |
| Error Saat Menggunakan Persamaan | Sintaks yang salah, penggunaan tanda kurung yang tidak tepat. | Periksa sintaks, gunakan tanda kurung dengan tepat, perbaiki persamaan. |
Latihan dan Contoh Soal
Kemampuan menulis rumus matematika di Word akan sangat berguna jika dipraktikkan secara langsung. Latihan soal dan contoh penyelesaian akan memperkuat pemahaman dan memberikan kepercayaan diri dalam menggunakan fitur-fitur yang telah dipelajari. Bagian ini akan menyajikan berbagai contoh soal matematika, tingkat kesulitan yang berbeda, serta akses untuk mengunduh soal latihan. Tujuannya adalah untuk memberikan pengalaman belajar yang komprehensif dan praktis.
Contoh Soal dan Penyelesaian Menggunakan Word
Mari kita mulai dengan contoh soal sederhana beserta cara penyelesaiannya menggunakan Word. Contoh ini akan menunjukkan bagaimana menggunakan berbagai fitur, mulai dari penulisan pecahan hingga penggunaan simbol matematika.
Contoh Soal: Selesaikan persamaan berikut: 1/ 2x + 3 = 7
Penyelesaian:
- Buka dokumen Word dan masukkan persamaan. Gunakan fitur “Equation” (Sisipkan > Simbol > Persamaan) untuk memulai.
- Ketikkan “1/2x + 3 = 7”. Untuk membuat pecahan, gunakan template pecahan yang tersedia di menu “Equation” atau ketikkan langsung dengan format a/b.
- Selesaikan persamaan secara manual atau dengan bantuan Word.
- Kurangkan kedua sisi dengan 3: 1/ 2x = 4
- Kalikan kedua sisi dengan 2: x = 8
- Hasil akhir: x = 8
Ilustrasi Deskriptif:
Ilustrasi ini menggambarkan langkah-langkah penyelesaian soal di atas dalam format yang menarik. Pertama, terdapat kotak yang menampilkan soal asli dengan jelas, menggunakan format pecahan yang rapi dan simbol matematika yang tepat. Di bawahnya, terdapat beberapa langkah penyelesaian, masing-masing dijelaskan dengan rinci. Setiap langkah dilengkapi dengan simbol matematika yang relevan, seperti tanda tambah, kurang, kali, dan bagi, serta tanda sama dengan.
Teks yang digunakan mudah dibaca dan berwarna agar lebih menarik. Di bagian akhir, terdapat kotak yang menyoroti jawaban akhir, yaitu x = 8, yang ditulis dengan huruf tebal untuk penekanan.
Latihan Soal dengan Tingkat Kesulitan Berbeda
Berikut adalah beberapa contoh soal latihan dengan tingkat kesulitan yang bervariasi untuk menguji kemampuan Anda dalam menggunakan Word.
- Soal Mudah: Hitung luas lingkaran dengan jari-jari 5 cm.
- Soal Sedang: Selesaikan sistem persamaan linear berikut: 2x + y = 5 dan x – y = 1.
- Soal Sulit: Cari turunan pertama dari fungsi f(x) = x 2 + 3x – 4.
Setiap soal di atas dapat diselesaikan dengan menggunakan fitur persamaan di Word. Pastikan untuk memanfaatkan semua fitur yang telah dipelajari untuk menghasilkan penyelesaian yang rapi dan mudah dipahami.
Akses Soal yang Dapat Diunduh
Untuk memberikan kemudahan dalam berlatih, kami menyediakan soal-soal latihan yang dapat diunduh dalam format Word. File ini berisi berbagai soal matematika dengan tingkat kesulitan yang berbeda, serta ruang kosong untuk menuliskan penyelesaian.
Cara Mengakses:
- Unduh file latihan melalui tautan yang tersedia.
- Buka file tersebut di Word.
- Kerjakan soal-soal yang ada.
- Simpan hasil pekerjaan Anda.
Dengan adanya file yang dapat diunduh ini, diharapkan proses belajar menjadi lebih efisien dan terstruktur.
Kesimpulan Akhir
Dari penulisan pecahan hingga penyusunan matriks, dari pemanfaatan AutoCorrect hingga penyisipan rumus dari aplikasi lain, perjalanan kita telah mengungkap berbagai cara untuk menguasai penulisan rumus matematika di Word. Kemampuan ini bukan hanya tentang menguasai alat, tetapi juga tentang membuka potensi diri dalam menyajikan ide-ide matematika dengan jelas dan efektif.
Dengan panduan ini, diharapkan Anda dapat menciptakan dokumen yang tidak hanya informatif, tetapi juga mudah dipahami dan menarik. Selamat berkarya, dan semoga keterampilan baru ini membawa kesuksesan dalam setiap proyek yang Anda kerjakan!
FAQ Lengkap
Bagaimana cara mengakses fitur “Equation” di Word?
Fitur “Equation” biasanya dapat diakses melalui tab “Insert”, kemudian klik “Equation” di grup “Symbols”.
Apa perbedaan antara “Equation” dan “Insert Symbol”?
“Equation” digunakan untuk membuat rumus matematika kompleks dengan struktur yang tepat, sedangkan “Insert Symbol” digunakan untuk menyisipkan simbol-simbol individual.
Apakah ada cara cepat untuk memasukkan simbol matematika?
Ya, Anda dapat menggunakan shortcut keyboard, fitur AutoCorrect, atau menyimpan rumus yang sering digunakan sebagai entri di Word.
Bagaimana cara menulis pecahan di Word?
Gunakan fitur “Equation” dan pilih template pecahan, atau gunakan garis miring (/) untuk pecahan sederhana.
Bagaimana cara mengatasi masalah rumus yang tidak muncul dengan benar?
Periksa pengaturan tampilan rumus, pastikan font yang digunakan kompatibel, dan perbarui Word jika perlu.
