Cara Mencari Arah Vektor Panduan Lengkap Dan Aplikasi Praktis

Cara mencari arah vektor – Siap untuk menyelami dunia vektor? Memahami dan mencari arah vektor adalah kunci untuk membuka potensi tak terbatas dalam matematika, fisika, dan banyak bidang lainnya. Bayangkan, Anda memiliki kekuatan untuk mengendalikan gerakan, memahami navigasi, dan bahkan merancang dunia virtual yang realistis. Itu semua dimulai dengan penguasaan arah vektor.

Panduan ini akan membawa Anda dari dasar-dasar konsep vektor hingga aplikasi praktis yang mengagumkan. Kita akan membahas berbagai metode, mulai dari pendekatan geometris yang intuitif hingga aljabar yang kuat. Persiapkan diri Anda untuk menjelajahi bagaimana vektor digunakan dalam kehidupan sehari-hari, dari navigasi GPS hingga pengembangan game. Mari kita mulai petualangan seru ini!

Table of Contents

Memahami Dasar Arah Vektor

Vektor adalah konsep fundamental dalam matematika dan fisika, yang digunakan untuk merepresentasikan besaran yang memiliki nilai (magnitude) dan arah. Memahami vektor adalah kunci untuk menguasai banyak konsep lanjutan dalam ilmu pengetahuan dan teknologi. Artikel ini akan membahas dasar-dasar arah vektor, mulai dari definisi hingga aplikasinya dalam berbagai bidang.

Definisi dan Representasi Vektor

Vektor adalah entitas matematika yang memiliki dua properti utama: besaran (magnitude) dan arah. Besaran adalah ukuran dari vektor (misalnya, panjang, kecepatan, atau gaya), sedangkan arah menunjukkan orientasi vektor dalam ruang. Vektor biasanya direpresentasikan secara grafis sebagai panah, di mana panjang panah mewakili besaran, dan arah panah menunjukkan arah vektor.

Notasi yang umum digunakan untuk vektor adalah huruf tebal ( v) atau huruf dengan tanda panah di atasnya (⃗v). Misalnya, vektor yang merepresentasikan perpindahan 5 meter ke timur dapat ditulis sebagai s = (5, 0), jika kita menggunakan sistem koordinat kartesius dengan sumbu x ke timur dan sumbu y ke utara. Komponen vektor (5,0) menunjukkan bahwa vektor memiliki nilai 5 pada sumbu x dan 0 pada sumbu y.

Contoh Penggunaan Arah Vektor dalam Kehidupan Sehari-hari

Arah vektor hadir dalam banyak aspek kehidupan sehari-hari, meskipun kita mungkin tidak selalu menyadarinya. Berikut adalah beberapa contoh sederhana:

Navigasi: Ketika menggunakan GPS atau peta, arah vektor digunakan untuk menentukan rute dari satu lokasi ke lokasi lain. Vektor menunjukkan arah dan jarak yang harus ditempuh.
Permainan: Dalam permainan video, arah vektor digunakan untuk mengontrol gerakan karakter, lintasan proyektil, dan arah gaya yang diterapkan pada objek.
Olahraga: Dalam olahraga seperti sepak bola atau bola basket, arah vektor digunakan untuk menganalisis lintasan bola, kecepatan pemain, dan arah gerakan.
Pengiriman Barang: Perusahaan pengiriman menggunakan arah vektor untuk merencanakan rute pengiriman barang, memperhitungkan jarak, dan waktu tempuh.

Perbedaan Skalar dan Vektor

Perbedaan mendasar antara skalar dan vektor terletak pada sifatnya. Skalar hanya memiliki besaran, sedangkan vektor memiliki besaran dan arah. Berikut adalah tabel yang merangkum perbedaan antara skalar dan vektor, beserta contohnya:

Karakteristik	Skalar	Vektor
Definisi	Besaran yang hanya memiliki nilai.	Besaran yang memiliki nilai dan arah.
Contoh	Massa, waktu, suhu, energi.	Perpindahan, kecepatan, gaya, percepatan.
Representasi	Angka tunggal.	Panah (grafis) atau komponen (matematis).
Operasi	Operasi aritmatika biasa (penjumlahan, pengurangan, perkalian, pembagian).	Penjumlahan, pengurangan, perkalian skalar, perkalian titik, perkalian silang.

Representasi Grafis Vektor

Vektor direpresentasikan secara grafis sebagai panah. Panjang panah menunjukkan besaran vektor, dan arah panah menunjukkan arah vektor. Untuk merepresentasikan vektor dalam sistem koordinat kartesius (misalnya, sumbu x dan y), kita menggunakan komponen vektor. Misalnya, vektor v = (3, 4) berarti vektor memiliki komponen 3 pada sumbu x dan 4 pada sumbu y.

Ilustrasi Deskriptif:

Bayangkan sebuah sistem koordinat kartesius. Vektor v = (3, 4) akan digambarkan sebagai panah yang dimulai dari titik asal (0, 0) dan berakhir di titik (3, 4). Panjang panah dapat dihitung menggunakan teorema Pythagoras: √(3² + 4²) = 5. Sudut yang dibentuk vektor dengan sumbu x positif dapat dihitung menggunakan fungsi trigonometri, misalnya arctan(4/3) ≈ 53.1 derajat. Dengan demikian, vektor ini memiliki besaran 5 dan arah sekitar 53.1 derajat terhadap sumbu x positif.

Pentingnya Arah Vektor dalam Ilmu Pengetahuan dan Teknologi

Arah vektor sangat penting dalam berbagai bidang ilmu pengetahuan dan teknologi. Beberapa contohnya meliputi:

Fisika: Vektor digunakan untuk menggambarkan gaya, kecepatan, percepatan, momentum, dan kuantitas fisika lainnya yang memiliki besaran dan arah. Hukum Newton tentang gerak, misalnya, sangat bergantung pada konsep vektor.
Teknik: Dalam teknik, vektor digunakan dalam analisis struktur, dinamika fluida, dan rekayasa listrik. Misalnya, analisis gaya pada jembatan atau pesawat terbang menggunakan konsep vektor.
Grafika Komputer: Vektor digunakan untuk merepresentasikan objek 3D, menentukan posisi dan orientasi objek, dan melakukan transformasi seperti rotasi dan translasi.
Robotika: Vektor digunakan untuk mengontrol gerakan robot, menghitung posisi dan orientasi lengan robot, dan merencanakan jalur gerakan.
Navigasi dan Pemetaan: GPS, peta digital, dan sistem navigasi lainnya menggunakan vektor untuk menentukan posisi, arah, dan jarak.

Metode Pencarian Arah Vektor: Cara Mencari Arah Vektor

Memahami arah vektor adalah kunci untuk memecahkan berbagai masalah di bidang fisika, teknik, dan bahkan navigasi sehari-hari. Berbagai metode telah dikembangkan untuk menentukan arah vektor, mulai dari pendekatan geometris yang intuitif hingga metode aljabar yang lebih canggih. Artikel ini akan membahas secara mendalam tentang metode geometris, memberikan panduan langkah demi langkah, contoh kasus, dan demonstrasi penggunaan alat bantu untuk mempermudah pemahaman.

Metode geometris menawarkan cara visual dan intuitif untuk menentukan arah vektor. Pendekatan ini memanfaatkan konsep sudut, koordinat, dan hubungan geometris untuk mengidentifikasi arah vektor dalam ruang.

Memahami arah vektor sangat krusial, mulai dari navigasi hingga fisika. Salah satu cara paling ampuh adalah dengan menggunakan trigonometri, memanfaatkan fungsi sinus, kosinus, dan tangen. Namun, jika Anda ingin mencari informasi lain yang relevan dan lebih spesifik, seperti detail tentang identitas diri di dunia digital, Anda bisa langsung meluncur ke Identif.id. Setelah itu, Anda bisa kembali fokus pada soal arah vektor, memastikan semua sudut dan komponen vektor telah terpecahkan dengan tepat.

Pendekatan Geometris: Sudut dan Koordinat

Pendekatan geometris untuk menentukan arah vektor berpusat pada penggunaan sudut dan koordinat. Ini melibatkan representasi vektor dalam sistem koordinat, seperti sistem koordinat Kartesius (x, y) atau koordinat polar (r, θ). Dengan menggunakan informasi ini, arah vektor dapat ditentukan dengan tepat.

Oke, mari kita mulai dengan mencari arah vektor, yang bisa jadi sedikit rumit. Tapi, setelah otak kita bekerja keras, tak ada salahnya memanjakan diri dengan sesuatu yang manis, kan? Bayangkan, setelah berjuang keras, kamu bisa langsung mencoba cara membuat popcorn manis sederhana. Setelah perut kenyang dan pikiran segar, kembali lagi ke soal arah vektor, dengan semangat baru! Dijamin, semuanya akan terasa lebih mudah.

Sistem Koordinat Kartesius: Dalam sistem ini, vektor direpresentasikan sebagai pasangan koordinat (x, y). Arah vektor dapat ditentukan dengan menghitung sudut yang dibentuk vektor dengan sumbu x positif. Sudut ini dapat dihitung menggunakan fungsi trigonometri seperti arctan(y/x).
Sistem Koordinat Polar: Dalam sistem ini, vektor direpresentasikan oleh panjang (r) dan sudut (θ) relatif terhadap sumbu referensi. Arah vektor secara langsung ditentukan oleh sudut θ.
Penggunaan Sudut: Sudut antara vektor dan sumbu referensi (misalnya, sumbu x) sangat penting. Sudut ini sering diukur dalam derajat atau radian, dan memberikan informasi tentang orientasi vektor dalam ruang.

Menghitung Sudut Antara Dua Vektor Menggunakan Dot Product

Salah satu cara yang ampuh untuk menentukan arah relatif antara dua vektor adalah dengan menggunakan konsep dot product (perkalian titik). Dot product menghasilkan nilai skalar yang terkait dengan sudut antara dua vektor.

Berikut adalah langkah-langkah untuk menghitung sudut antara dua vektor menggunakan rumus dot product:

Tentukan Vektor: Diberikan dua vektor, misalnya, A = (Ax, Ay) dan B = (Bx, By).
Hitung Dot Product: Hitung dot product dari dua vektor tersebut menggunakan rumus: A · B = Ax
- Bx + Ay
- By.
Hitung Magnitudo Vektor: Hitung magnitudo (panjang) dari masing-masing vektor: | A| = √(Ax² + Ay²) dan | B| = √(Bx² + By²).
Gunakan Rumus Sudut: Gunakan rumus berikut untuk menghitung sudut θ antara dua vektor:

θ = arccos((A · B) / (| A| – | B|))

Rumus ini memberikan sudut dalam radian. Untuk mengubahnya ke derajat, kalikan hasilnya dengan 180/π.

Rumus dot product memberikan cara yang efisien untuk menentukan sudut antara dua vektor, yang sangat berguna dalam berbagai aplikasi fisika dan teknik.

Contoh Kasus Penggunaan dalam Pemecahan Masalah Fisika

Metode geometris sangat berguna dalam pemecahan masalah fisika, khususnya dalam menganalisis gaya, kecepatan, dan percepatan. Berikut adalah contoh kasus:

Contoh: Dua gaya, F1 = (3, 4) N dan F2 = (5, -2) N, bekerja pada suatu objek. Tentukan arah resultan gaya.

Hitung Resultan Gaya: Resultan gaya, F, adalah jumlah vektor dari kedua gaya: F = F1 + F2 = (3+5, 4-2) = (8, 2) N.
Hitung Sudut: Hitung sudut θ yang dibentuk resultan gaya dengan sumbu x positif. Gunakan arctan: θ = arctan(2/8) ≈ 14.04 derajat.
Kesimpulan: Arah resultan gaya adalah sekitar 14.04 derajat relatif terhadap sumbu x positif.

Contoh ini menunjukkan bagaimana metode geometris, dikombinasikan dengan perhitungan sederhana, dapat memberikan informasi yang akurat tentang arah dan besaran gaya resultan.

Penggunaan Software dan Alat Bantu Grafis

Software dan alat bantu grafis sangat mempermudah visualisasi dan perhitungan arah vektor secara geometris. Alat-alat ini memungkinkan pengguna untuk memvisualisasikan vektor, melakukan perhitungan, dan memverifikasi hasil dengan cepat dan akurat.

Geogebra: Software matematika interaktif yang memungkinkan pengguna untuk menggambar vektor, melakukan operasi vektor, dan menghitung sudut. Visualisasi yang jelas membantu dalam memahami konsep.
Desmos: Kalkulator grafik online yang juga mendukung representasi vektor. Pengguna dapat dengan mudah memasukkan koordinat vektor dan melihat hasilnya secara visual.
Software CAD (Computer-Aided Design): Software seperti AutoCAD atau SolidWorks digunakan dalam teknik untuk menggambar dan menganalisis objek 2D dan 3D. Software ini memiliki kemampuan untuk menghitung dan menampilkan arah vektor.

Penggunaan alat-alat ini mempercepat proses perhitungan dan membantu dalam memahami konsep geometris secara lebih mendalam.

Penerapan Metode Geometris dalam Navigasi dan Pemetaan

Metode geometris memainkan peran penting dalam navigasi dan pemetaan. Pengetahuan tentang arah vektor sangat penting dalam menentukan posisi, jalur, dan orientasi.

Navigasi: Dalam navigasi, arah vektor digunakan untuk menentukan arah dan jarak. Sistem GPS menggunakan prinsip-prinsip geometris untuk menghitung posisi berdasarkan sinyal dari satelit.
Pemetaan: Dalam pemetaan, arah vektor digunakan untuk merepresentasikan orientasi dan arah fitur geografis. Data yang dikumpulkan oleh survei dan sensor seringkali direpresentasikan sebagai vektor.
Kompas dan Penentu Arah: Kompas menggunakan prinsip magnetik untuk menunjukkan arah, yang dapat direpresentasikan sebagai vektor. Penentu arah seperti giroskop juga menggunakan konsep vektor untuk memberikan informasi orientasi.

Contohnya, seorang navigator kapal menggunakan kompas dan peta (yang menggunakan sistem koordinat) untuk menentukan arah dan jarak ke tujuan. Penggunaan metode geometris memastikan navigasi yang akurat dan efisien.

Metode Pencarian Arah Vektor: Cara Mencari Arah Vektor

Dalam dunia matematika dan fisika, menentukan arah vektor adalah keterampilan fundamental. Meskipun terdapat berbagai pendekatan, metode aljabar menonjol karena ketepatannya dan kemampuannya untuk menangani masalah yang kompleks. Artikel ini akan mengupas tuntas metode aljabar untuk mencari arah vektor, mulai dari konsep dasar hingga aplikasinya dalam bidang-bidang seperti pemrosesan sinyal dan grafika komputer.

Mari kita selami lebih dalam bagaimana metode aljabar membuka cara pandang baru dalam memahami dan memanipulasi vektor.

Metode Pencarian Arah Vektor: Pendekatan Aljabar

Metode aljabar menawarkan cara yang sistematis dan presisi untuk menentukan arah vektor. Pendekatan ini berfokus pada dekomposisi vektor menjadi komponen-komponennya dan penggunaan operasi vektor untuk menemukan sudut atau arah yang diinginkan. Keunggulan metode ini terletak pada kemampuannya untuk menghasilkan solusi yang konsisten dan dapat diandalkan, bahkan dalam kasus yang melibatkan vektor dalam ruang dimensi yang lebih tinggi.

Memahami arah vektor memang krusial, ibarat navigasi di lautan ilmu pengetahuan. Kita perlu ketelitian dalam menghitung komponen-komponennya. Namun, semangat untuk terus belajar dan berkembang adalah kunci utama. Seperti halnya semangat yang membara dalam Sambutan Hari Pendidikan Nasional: Membangun Generasi Unggul untuk Indonesia Maju , yang mendorong kita untuk terus meningkatkan kualitas pendidikan. Dengan begitu, kita bisa dengan lebih mudah menentukan arah vektor yang tepat dan mencapai tujuan yang kita impikan.

Berikut adalah beberapa aspek penting dalam metode aljabar:

Komponen Vektor: Vektor dapat diuraikan menjadi komponen-komponennya sepanjang sumbu koordinat (misalnya, sumbu x dan y dalam ruang dua dimensi, atau x, y, dan z dalam ruang tiga dimensi). Komponen-komponen ini merupakan proyeksi vektor pada masing-masing sumbu.
Operasi Vektor: Operasi vektor, seperti penjumlahan, pengurangan, dan perkalian skalar, digunakan untuk memanipulasi komponen vektor dan menemukan informasi tentang arahnya.
Fungsi Trigonometri: Fungsi trigonometri (sinus, kosinus, tangen, dan inversnya) digunakan untuk menghitung sudut yang dibentuk vektor terhadap sumbu koordinat.

Langkah-Langkah Menghitung Komponen Vektor

Untuk menghitung komponen vektor, ikuti langkah-langkah berikut:

Identifikasi Vektor: Tentukan vektor yang akan dianalisis, termasuk besaran (magnitude) dan arahnya. Arah biasanya diberikan dalam bentuk sudut terhadap sumbu referensi (misalnya, sumbu x positif).
Gunakan Rumus Komponen: Gunakan rumus berikut untuk menghitung komponen vektor:
- Komponen x: V _x = |V|
  – cos(θ)
- Komponen y: V _y = |V|
  – sin(θ)
Di mana:
- |V| adalah besaran vektor.
- θ adalah sudut antara vektor dan sumbu x positif.
Hitung Komponen: Masukkan nilai besaran dan sudut ke dalam rumus untuk menghitung nilai komponen x dan y.
Representasi Komponen: Nyatakan vektor dalam bentuk komponennya, misalnya, V = (V _x, V _y).

Dengan mengikuti langkah-langkah ini, Anda dapat dengan mudah menguraikan vektor menjadi komponen-komponennya, yang sangat penting dalam banyak perhitungan dan aplikasi.

Contoh Kasus Penggunaan Metode Aljabar

Mari kita lihat contoh kasus penggunaan metode aljabar dalam pemecahan masalah matematika. Misalkan kita memiliki sebuah vektor gaya dengan besaran 10 N yang membentuk sudut 30 derajat terhadap sumbu x positif. Kita akan menghitung komponen x dan y dari vektor gaya ini.

Perhitungan:

Komponen x: F _x = |F|
– cos(θ) = 10 N
– cos(30°) ≈ 8.66 N
Komponen y: F _y = |F|
– sin(θ) = 10 N
– sin(30°) = 5 N

Dengan demikian, vektor gaya dapat direpresentasikan sebagai (8.66 N, 5 N). Perhitungan ini menunjukkan bagaimana metode aljabar memungkinkan kita untuk menguraikan gaya menjadi komponen-komponen yang mempermudah analisis dan perhitungan lebih lanjut, seperti dalam menentukan percepatan atau efek gaya pada suatu objek.

Memahami arah vektor memang krusial, mulai dari fisika hingga teknik. Namun, fondasi kuat dalam bidang ini tak lepas dari kualitas Pendidikan yang kita terima. Dengan pemahaman yang baik, kita bisa lebih mudah memvisualisasikan dan menghitung arah vektor, yang pada akhirnya mempermudah penyelesaian masalah. Jadi, jangan remehkan pentingnya menguasai konsep dasar untuk menemukan arah vektor yang tepat.

Perbandingan Metode Geometris dan Aljabar

Berikut adalah tabel yang membandingkan metode geometris dan aljabar dalam mencari arah vektor:

Fitur	Metode Geometris	Metode Aljabar
Pendekatan	Menggunakan representasi visual dan pengukuran.	Menggunakan perhitungan matematis berdasarkan komponen vektor.
Akurasi	Tergantung pada presisi gambar dan pengukuran.	Tinggi, berdasarkan perhitungan matematis.
Kompleksitas	Sederhana untuk vektor dalam dua dimensi.	Cocok untuk vektor dalam berbagai dimensi.
Kemudahan Penggunaan	Mudah dipahami secara visual.	Membutuhkan pemahaman tentang aljabar vektor dan trigonometri.
Keterbatasan	Sulit untuk vektor dalam dimensi tinggi. Rentan terhadap kesalahan pengukuran.	Membutuhkan perhitungan yang lebih rumit untuk beberapa kasus.

Tabel ini memberikan gambaran yang jelas tentang perbedaan antara kedua metode, yang membantu dalam memilih pendekatan yang paling sesuai untuk situasi tertentu.

Metode Aljabar dalam Pemrosesan Sinyal dan Grafika Komputer

Metode aljabar memainkan peran penting dalam pemrosesan sinyal dan grafika komputer. Dalam pemrosesan sinyal, vektor digunakan untuk merepresentasikan sinyal, dan operasi vektor digunakan untuk melakukan transformasi seperti filtering dan analisis frekuensi. Misalnya, transformasi Fourier, yang sangat penting dalam analisis sinyal, melibatkan penggunaan operasi vektor untuk menguraikan sinyal menjadi komponen-komponen frekuensinya.

Dalam grafika komputer, vektor digunakan untuk merepresentasikan posisi, arah, dan warna. Operasi vektor seperti rotasi, translasi, dan penskalaan digunakan untuk memanipulasi objek 3D. Contohnya, saat merender adegan 3D, transformasi matriks (yang merupakan representasi aljabar dari operasi vektor) digunakan untuk mengubah posisi dan orientasi objek dalam ruang 3D. Tanpa metode aljabar, implementasi aplikasi-aplikasi ini akan sangat sulit atau bahkan tidak mungkin dilakukan.

Aplikasi Praktis Arah Vektor

Arah vektor, konsep fundamental dalam matematika dan fisika, memiliki penerapan yang luas di berbagai bidang. Pemahaman tentang arah vektor memungkinkan kita untuk memodelkan dan mengontrol gerakan, posisi, dan interaksi dalam dunia nyata dan digital. Dari navigasi GPS yang kita gunakan sehari-hari hingga pengembangan game yang imersif, arah vektor adalah tulang punggung dari banyak teknologi modern.

Mari kita selami beberapa aplikasi praktis arah vektor yang paling menonjol.

Memahami arah vektor memang krusial, ibarat navigasi tanpa kompas. Tapi, tahukah kamu, menyusun langkah-langkah belajar yang tepat juga sama pentingnya? Itulah mengapa RPP (Rencana Pelaksanaan Pembelajaran) hadir, sebagai peta jalan. Sama seperti kita mencari arah vektor dengan rumus-rumus, RPP membantu guru mengarahkan pembelajaran agar lebih efektif. Dengan begitu, kita bisa menemukan arah yang tepat, baik dalam fisika maupun dalam pendidikan.

Navigasi GPS dan Perhitungan Posisi

Sistem Penentuan Posisi Global (GPS) adalah contoh utama bagaimana arah vektor digunakan secara praktis. GPS memanfaatkan satelit yang mengorbit Bumi untuk menentukan lokasi pengguna dengan presisi tinggi. Proses ini melibatkan perhitungan jarak antara penerima GPS dan beberapa satelit sekaligus, menggunakan prinsip triangulasi.

Berikut adalah cara arah vektor digunakan dalam navigasi GPS:

Pengukuran Jarak: Setiap satelit GPS mengirimkan sinyal radio yang berisi informasi waktu. Penerima GPS mengukur waktu tempuh sinyal tersebut. Dengan mengetahui kecepatan rambat sinyal (kecepatan cahaya) dan waktu tempuh, jarak antara satelit dan penerima dapat dihitung.
Vektor Posisi Satelit: Setiap satelit GPS memiliki posisi yang diketahui secara tepat di ruang angkasa. Posisi ini direpresentasikan sebagai vektor.
Triangulasi: Penerima GPS menggunakan informasi jarak dari setidaknya tiga satelit untuk menentukan posisinya di Bumi. Setiap satelit memberikan informasi tentang kemungkinan lokasi penerima, membentuk sebuah bola dengan satelit sebagai pusat dan jarak sebagai jari-jari. Perpotongan dari tiga bola ini (atau lebih) menentukan lokasi penerima.
Perhitungan Arah dan Kecepatan: Setelah posisi ditentukan, GPS dapat menghitung arah pergerakan dan kecepatan pengguna dengan membandingkan posisi saat ini dengan posisi sebelumnya. Perubahan posisi dari waktu ke waktu direpresentasikan sebagai vektor kecepatan.

Simulasi Gerakan Objek

Simulasi gerakan objek adalah aplikasi penting lainnya dari arah vektor, terutama dalam bidang seperti animasi komputer, simulasi fisika, dan pengembangan game. Arah vektor digunakan untuk menentukan bagaimana objek bergerak dalam ruang 2D atau 3D, termasuk kecepatan, arah, dan percepatan.

Simulasi sederhana dapat dibuat dengan menggunakan konsep berikut:

Posisi: Posisi objek diwakili oleh vektor posisi (x, y) dalam ruang 2D atau (x, y, z) dalam ruang 3D.
Kecepatan: Kecepatan objek diwakili oleh vektor kecepatan. Vektor ini menentukan seberapa cepat dan ke arah mana objek bergerak.
Percepatan: Percepatan objek diwakili oleh vektor percepatan. Percepatan mengubah kecepatan objek dari waktu ke waktu.
Update Posisi: Posisi objek diperbarui secara berkala berdasarkan kecepatan dan percepatannya. Rumus dasarnya adalah:

Posisi Baru = Posisi Lama + (Kecepatan
– Waktu)

Dalam simulasi, waktu biasanya dibagi menjadi langkah-langkah kecil (misalnya, setiap 1/60 detik). Pada setiap langkah, posisi objek diperbarui berdasarkan kecepatan dan percepatannya. Dengan mengulangi proses ini, kita dapat mensimulasikan gerakan objek yang realistis.

Sebagai contoh, bayangkan sebuah bola yang bergerak di lingkungan 2D. Vektor kecepatan bola menentukan arah dan kecepatan bola bergerak. Jika ada gaya gravitasi (misalnya, dalam simulasi fisika), vektor percepatan akan ditambahkan ke kecepatan bola setiap langkah waktu, menyebabkan bola jatuh ke bawah.

Arah Vektor dalam Pengembangan Game

Pengembangan game sangat bergantung pada arah vektor untuk menciptakan pengalaman yang imersif dan interaktif. Arah vektor digunakan untuk berbagai aspek, mulai dari gerakan karakter hingga deteksi tabrakan.

Arah vektor dalam pengembangan game memainkan peran penting dalam menentukan arah gerakan karakter, proyeksi peluru, dan perhitungan jalur.

Berikut adalah beberapa contoh penggunaan arah vektor dalam pengembangan game:

Gerakan Karakter: Arah vektor digunakan untuk menentukan arah gerakan karakter dalam game. Misalnya, jika pemain menekan tombol “maju”, karakter akan bergerak ke arah yang ditentukan oleh vektor arah.
Proyeksi Peluru: Ketika pemain menembakkan peluru, arah vektor digunakan untuk menentukan lintasan peluru. Vektor ini menentukan kecepatan dan arah awal peluru.
Deteksi Tabrakan: Arah vektor dapat digunakan untuk mendeteksi tabrakan antara objek dalam game. Dengan membandingkan posisi dan arah vektor objek, game dapat menentukan apakah objek tersebut bertabrakan.
AI dan Perilaku Karakter: Kecerdasan buatan (AI) dalam game menggunakan arah vektor untuk menentukan perilaku karakter non-pemain (NPC). Misalnya, NPC dapat menggunakan arah vektor untuk mengejar pemain, menghindari rintangan, atau bergerak ke tujuan tertentu.

Kontrol Gerak Robot

Arah vektor memainkan peran krusial dalam kontrol gerak robot, memungkinkan robot untuk bergerak secara presisi dan efektif. Ini mencakup perencanaan jalur, pengendalian, dan navigasi.

Memahami arah vektor memang krusial, mulai dari fisika hingga grafis. Untuk memulainya, Anda perlu menguasai konsep dasar seperti komponen vektor dan trigonometri. Nah, jika Anda ingin memperdalam pengetahuan tentang teknologi dan inovasi, jangan lewatkan Identif , platform yang menyajikan berita dan analisis mendalam. Dengan begitu, Anda akan memiliki bekal yang lebih baik dalam mencari dan memahami arah vektor dalam berbagai konteks.

Berikut adalah beberapa aplikasi spesifik:

Perencanaan Jalur: Arah vektor digunakan untuk merencanakan jalur yang akan dilalui robot. Algoritma perencanaan jalur sering kali menggunakan vektor untuk menentukan titik-titik lintasan, menghindari rintangan, dan mengoptimalkan perjalanan.
Pengendalian Motor: Robot menggunakan motor untuk menggerakkan roda atau anggota tubuhnya. Arah vektor digunakan untuk mengendalikan motor-motor ini, menentukan kecepatan dan arah putaran mereka.
Navigasi: Robot menggunakan sensor (seperti kamera atau sensor ultrasonik) untuk merasakan lingkungannya. Arah vektor digunakan untuk menginterpretasikan data sensor ini dan menentukan posisi dan arah robot.
Kontrol Gerak Presisi: Dalam tugas-tugas seperti perakitan atau manipulasi objek, arah vektor digunakan untuk memastikan gerakan robot presisi dan sesuai dengan tujuan. Robot dapat menggunakan vektor untuk mengontrol posisi dan orientasi ujung lengan robot (end-effector).

Tantangan dan Tips dalam Mencari Arah Vektor

Mencari arah vektor, meskipun tampak sederhana, seringkali diwarnai oleh berbagai tantangan. Ketidakpastian dalam pengukuran, kesalahan perhitungan, dan kurangnya pemahaman konsep dasar dapat menghambat proses ini. Bagian ini akan membahas tantangan umum, memberikan tips untuk menghindarinya, serta menyajikan sumber daya dan saran untuk meningkatkan kemampuan dalam mencari arah vektor.

Tantangan Umum dalam Mencari Arah Vektor, Cara mencari arah vektor

Proses penentuan arah vektor seringkali menemui hambatan yang perlu diatasi. Beberapa tantangan utama meliputi:

Ketidakpastian Pengukuran: Pengukuran fisik, seperti panjang dan sudut, selalu memiliki tingkat ketidakpastian. Ketidakpastian ini dapat berasal dari alat ukur yang kurang presisi, kesalahan manusia, atau kondisi lingkungan yang mempengaruhi pengukuran. Misalnya, penggunaan penggaris biasa untuk mengukur panjang akan memiliki ketidakpastian yang lebih besar dibandingkan dengan penggunaan caliper digital.
Kesalahan Perhitungan: Kesalahan perhitungan dapat terjadi dalam berbagai tahap, mulai dari penggunaan rumus yang salah hingga kesalahan dalam memasukkan data ke dalam kalkulator. Kesalahan ini dapat mengakibatkan hasil yang sangat berbeda dari nilai sebenarnya. Sebagai contoh, kesalahan dalam mengalikan atau membagi komponen vektor dapat mengubah arah dan magnitudo vektor akhir secara signifikan.
Pemahaman Konsep yang Kurang: Kurangnya pemahaman tentang konsep dasar vektor, seperti penjumlahan, pengurangan, dan dekomposisi vektor, dapat menghambat kemampuan untuk mencari arah vektor dengan benar. Pemahaman yang buruk tentang konsep-konsep ini dapat menyebabkan kebingungan dalam memilih metode yang tepat atau menafsirkan hasil perhitungan.
Kompleksitas Sistem: Dalam sistem yang lebih kompleks, seperti dalam navigasi atau analisis gaya pada suatu objek, mencari arah vektor dapat menjadi rumit karena melibatkan banyak vektor yang saling berinteraksi. Memahami bagaimana vektor-vektor ini berinteraksi dan bagaimana mereka memengaruhi satu sama lain adalah kunci untuk menentukan arah vektor yang benar.

Tips Menghindari Kesalahan Perhitungan Arah Vektor

Untuk meminimalkan kesalahan dalam perhitungan arah vektor, beberapa tips berikut dapat diterapkan:

Gunakan Alat Ukur yang Tepat: Pilih alat ukur yang sesuai dengan tingkat presisi yang dibutuhkan. Jika presisi tinggi diperlukan, gunakan alat ukur yang lebih canggih, seperti caliper digital atau theodolite.
Periksa Ulang Pengukuran: Lakukan pengukuran beberapa kali dan bandingkan hasilnya untuk mengidentifikasi outlier atau kesalahan. Lakukan pengukuran berulang dan catat hasilnya untuk memperkecil kemungkinan kesalahan.
Periksa Rumus dan Metode: Pastikan untuk menggunakan rumus dan metode yang benar sesuai dengan situasi yang dihadapi. Gunakan diagram vektor untuk memvisualisasikan masalah dan memastikan bahwa perhitungan dilakukan dengan benar.
Gunakan Software atau Kalkulator: Manfaatkan software atau kalkulator yang dirancang untuk perhitungan vektor. Software ini dapat membantu mengurangi kesalahan perhitungan dan memberikan hasil yang lebih akurat.
Perhatikan Satuan: Pastikan semua satuan konsisten. Konversikan semua satuan ke satuan yang sama sebelum melakukan perhitungan. Misalnya, pastikan semua panjang diukur dalam meter dan semua sudut dalam derajat atau radian.
Lakukan Pengecekan Hasil: Setelah mendapatkan hasil, lakukan pengecekan untuk memastikan bahwa hasil tersebut masuk akal. Bandingkan hasil dengan perkiraan awal atau gunakan metode alternatif untuk memverifikasi.

Sumber Daya Belajar Tambahan

Untuk meningkatkan pemahaman tentang arah vektor, berbagai sumber daya belajar tersedia:

Buku Teks Fisika dan Matematika: Buku teks fisika dan matematika menyediakan penjelasan komprehensif tentang konsep vektor, termasuk cara mencari arah vektor. Buku-buku ini seringkali dilengkapi dengan contoh soal dan latihan untuk membantu memahami konsep.
Video Tutorial Online: Platform seperti YouTube menawarkan banyak video tutorial yang menjelaskan konsep vektor secara visual. Video-video ini seringkali menampilkan contoh soal yang diselesaikan langkah demi langkah.
Situs Web Interaktif: Situs web interaktif menyediakan simulasi dan latihan yang memungkinkan pengguna untuk mempraktikkan konsep vektor secara langsung. Beberapa situs web juga menawarkan kuis dan tes untuk menguji pemahaman.
Kursus Online: Kursus online, baik berbayar maupun gratis, menawarkan pembelajaran terstruktur tentang vektor dan konsep terkait. Kursus-kursus ini seringkali mencakup video, kuis, dan forum diskusi.

Pertanyaan yang Sering Diajukan (FAQ) tentang Arah Vektor

Berikut adalah beberapa pertanyaan yang sering diajukan tentang konsep dan aplikasi arah vektor:

Apa itu vektor? Vektor adalah besaran yang memiliki magnitudo (nilai) dan arah. Vektor dapat direpresentasikan secara grafis dengan anak panah, di mana panjang anak panah menunjukkan magnitudo dan arah anak panah menunjukkan arah vektor.
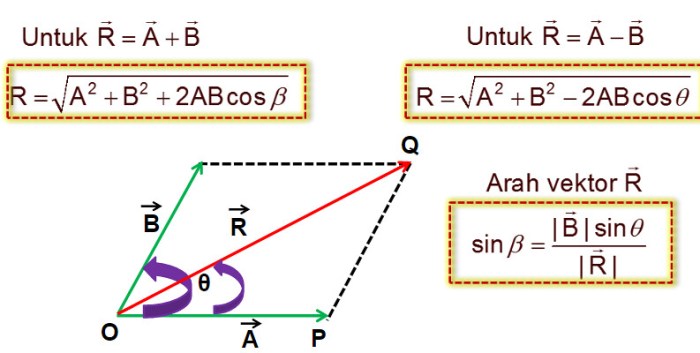
Bagaimana cara menjumlahkan vektor? Vektor dapat dijumlahkan dengan menggunakan metode jajar genjang atau metode ujung ke ujung. Pada metode jajar genjang, vektor-vektor ditempatkan sehingga pangkal mereka bertemu, dan kemudian dibuat jajar genjang dengan vektor-vektor sebagai sisinya. Diagonal jajar genjang dari pangkal yang sama adalah vektor resultan. Pada metode ujung ke ujung, vektor-vektor disusun sedemikian rupa sehingga ujung vektor pertama bertemu dengan pangkal vektor kedua, dan seterusnya.

Memahami arah vektor memang membutuhkan sedikit ketelitian, mirip seperti saat kita mencoba menemukan sudut yang tepat dalam navigasi. Tapi, setelah kita menguasainya, semua akan terasa lebih mudah. Sama halnya dengan cara memasak bacem ayam , awalnya mungkin terlihat rumit, namun dengan mengikuti langkah-langkah yang tepat, kita bisa menghasilkan hidangan lezat. Kembali lagi ke vektor, ketelitian dalam menentukan arah akan memandu kita menuju solusi yang tepat.

Vektor resultan ditarik dari pangkal vektor pertama ke ujung vektor terakhir.
Bagaimana cara menguraikan vektor? Vektor dapat diuraikan menjadi komponen-komponennya sepanjang sumbu koordinat (misalnya, sumbu x dan y). Proses ini melibatkan penggunaan fungsi trigonometri (sinus dan kosinus) untuk menghitung magnitudo komponen-komponen tersebut.
Apa saja aplikasi arah vektor? Arah vektor memiliki banyak aplikasi, termasuk dalam fisika (gaya, kecepatan, percepatan), navigasi (penentuan arah dan posisi), grafika komputer (rendering 3D), dan rekayasa (analisis struktur).
Bagaimana cara menentukan arah vektor resultan? Arah vektor resultan dapat ditentukan dengan menggunakan fungsi trigonometri, seperti tangen. Setelah menghitung komponen-komponen vektor resultan (Rx dan Ry), arah vektor resultan (θ) dapat dihitung dengan rumus: θ = arctan(Ry/Rx).

Meningkatkan Pemahaman dan Keterampilan

Untuk meningkatkan pemahaman dan keterampilan dalam mencari arah vektor, beberapa saran berikut dapat diikuti:

Latihan Soal Secara Teratur: Latihan soal secara teratur membantu memperkuat pemahaman konsep dan meningkatkan kemampuan dalam menyelesaikan masalah yang melibatkan arah vektor.
Gunakan Visualisasi: Gunakan diagram vektor untuk memvisualisasikan masalah. Visualisasi membantu memahami hubungan antara vektor dan mempermudah perhitungan.
Minta Bantuan: Jangan ragu untuk meminta bantuan dari guru, teman, atau sumber daya online jika mengalami kesulitan.
Terapkan Konsep: Coba terapkan konsep arah vektor dalam situasi dunia nyata. Ini dapat membantu memperkuat pemahaman dan membuat konsep lebih mudah diingat.
Pelajari Contoh Kasus: Pelajari contoh kasus nyata, seperti analisis gaya pada jembatan atau navigasi pesawat terbang, untuk melihat bagaimana konsep arah vektor diterapkan dalam praktik.

Kesimpulan

Kita telah menjelajahi dunia arah vektor, dari konsep dasar hingga aplikasi praktis yang mengagumkan. Telah dibahas bagaimana metode geometris dan aljabar dapat digunakan untuk mengungkap rahasia arah vektor, dan bagaimana konsep ini menjadi tulang punggung berbagai teknologi modern. Dengan pengetahuan ini, Anda sekarang memiliki alat untuk memecahkan masalah kompleks, merancang solusi inovatif, dan membuka pintu menuju dunia yang lebih dinamis dan terarah.

Ingatlah, menguasai arah vektor adalah perjalanan, bukan tujuan. Teruslah berlatih, bereksperimen, dan jelajahi potensi tak terbatas yang ditawarkan oleh dunia vektor. Sampai jumpa di petualangan matematika dan fisika selanjutnya!

FAQ Terpadu

Apa itu vektor?

Vektor adalah entitas matematika yang memiliki besar (magnitude) dan arah. Ini berbeda dari skalar, yang hanya memiliki besar.

Bagaimana cara merepresentasikan vektor secara grafis?

Vektor direpresentasikan sebagai panah. Panjang panah menunjukkan besar vektor, dan arah panah menunjukkan arah vektor.

Apa perbedaan antara metode geometris dan aljabar dalam mencari arah vektor?

Metode geometris menggunakan sudut dan koordinat untuk menentukan arah, sedangkan metode aljabar menggunakan komponen vektor dan operasi vektor.

Apa saja aplikasi praktis dari arah vektor?

Arah vektor digunakan dalam berbagai bidang, termasuk navigasi GPS, pengembangan game, robotika, desain grafis, dan pemrosesan sinyal.

Bagaimana cara menghitung sudut antara dua vektor?

Post Views: 1

Cara Mencari Arah Vektor Panduan Lengkap dan Aplikasi Praktis