Cara mengatasi uji normalitas eviews – Selamat datang dalam diskusi mendalam tentang cara mengatasi uji normalitas dalam EViews. Pernahkah Anda bertanya-tanya, mengapa uji normalitas begitu penting sebelum melakukan analisis regresi? Apakah data Anda benar-benar “normal”? Kita akan membahas tuntas, mulai dari dasar-dasar uji normalitas hingga strategi praktis untuk mengatasi masalah yang seringkali muncul dalam analisis data, khususnya ketika menggunakan EViews.
Uji normalitas adalah fondasi penting dalam analisis statistik, terutama dalam konteks regresi. Asumsi normalitas pada data memastikan bahwa hasil analisis regresi dapat diandalkan dan interpretasi yang dibuat valid. Pelanggaran asumsi ini dapat menyebabkan kesimpulan yang keliru, mempengaruhi nilai p, standar error, dan bahkan uji hipotesis. Mari kita selami lebih dalam untuk memahami bagaimana uji normalitas bekerja, konsekuensi dari pelanggaran, dan, yang terpenting, cara mengatasinya dengan efektif menggunakan EViews.
Pengantar Uji Normalitas dalam EViews
Uji normalitas adalah fondasi penting dalam analisis regresi, khususnya saat menggunakan perangkat lunak seperti EViews. Memahami uji ini memungkinkan kita memastikan keandalan hasil analisis dan menghindari kesimpulan yang menyesatkan. Artikel ini akan membahas secara mendalam tentang signifikansi, konsekuensi, dan interpretasi uji normalitas, memberikan landasan yang kuat untuk analisis data yang akurat dan valid.
1.1. Signifikansi Uji Normalitas
Uji normalitas memegang peranan krusial sebelum melakukan analisis regresi di EViews. Hal ini karena regresi linear klasik didasarkan pada sejumlah asumsi, dan salah satunya adalah asumsi bahwa residual (selisih antara nilai yang diamati dan nilai yang diprediksi oleh model) terdistribusi secara normal. Pelanggaran asumsi ini dapat mengganggu validitas hasil regresi.
- Mengapa uji normalitas penting? Uji normalitas memastikan bahwa residual memiliki distribusi yang mendekati distribusi normal. Distribusi normal adalah dasar dari banyak uji statistik inferensial. Jika residual tidak normal, nilai p (p-value) yang dihasilkan dari uji t, uji F, dan uji lainnya mungkin tidak akurat, yang dapat menyebabkan kesimpulan yang salah tentang hubungan antara variabel.
- Asumsi Klasik yang Terpengaruh: Pelanggaran asumsi normalitas terutama memengaruhi validitas uji hipotesis dan interval kepercayaan. Jika residual tidak normal, standar error koefisien regresi mungkin tidak akurat, yang berdampak pada perhitungan statistik uji dan interpretasi signifikansi variabel.
- Contoh Kasus Nyata: Dalam ekonomi, jika kita menganalisis hubungan antara pengeluaran konsumen dan pendapatan, pelanggaran normalitas dapat terjadi jika ada outlier yang signifikan. Dalam keuangan, model yang memprediksi harga saham dapat menghasilkan residual yang tidak normal karena volatilitas pasar yang tinggi. Dalam bidang sosial, survei kepuasan kerja dengan data yang sangat skewed (condong) juga dapat melanggar asumsi normalitas. Kesimpulan yang salah dapat diambil jika uji normalitas diabaikan, yang mengarah pada rekomendasi kebijakan yang tidak tepat.
Oke, mari kita bedah. Uji normalitas di EViews memang krusial, kan? Kalau datamu tidak normal, solusinya bisa transformasi data atau menggunakan metode lain. Tapi, pernahkah kamu terpikir, bagaimana caranya menyampaikan informasi penting ke banyak orang sekaligus? Misalnya, pengumuman penting terkait penelitianmu.
Nah, ada trik jitu nih, yaitu cara kirim pesan ke semua kontak wa , sangat berguna untuk koordinasi cepat. Kembali ke EViews, setelah data diolah, jangan lupa periksa lagi normalitasnya, ya. Pastikan asumsi terpenuhi agar hasil analisismu valid.
- Hubungan Uji Normalitas dan Validitas Regresi: Uji normalitas memastikan bahwa asumsi-asumsi statistik yang mendasari analisis regresi terpenuhi. Jika asumsi normalitas terpenuhi, hasil regresi (koefisien, nilai p, dan interval kepercayaan) lebih dapat diandalkan dan dapat digunakan untuk menarik kesimpulan yang valid tentang hubungan antar variabel. Jika tidak, kesimpulan yang diambil dari model regresi dapat menjadi bias dan menyesatkan.
1.2. Konsekuensi Pelanggaran Asumsi Normalitas
Pelanggaran asumsi normalitas dapat membawa konsekuensi signifikan terhadap hasil dan interpretasi model regresi. Dampaknya meluas ke berbagai aspek statistik dan interpretasi hasil.
- Dampak pada Statistik:
- Nilai p dan Tingkat Signifikansi: Pelanggaran normalitas dapat menyebabkan nilai p yang tidak akurat. Hal ini dapat mengakibatkan kesalahan dalam penentuan signifikansi statistik variabel, yang berarti variabel yang sebenarnya tidak signifikan dapat dianggap signifikan, atau sebaliknya.
- Standar Error Koefisien Regresi: Standar error koefisien regresi dapat menjadi bias jika asumsi normalitas dilanggar. Hal ini memengaruhi perhitungan statistik uji (seperti uji t) dan interval kepercayaan.
- Interval Kepercayaan: Interval kepercayaan yang dihitung berdasarkan asumsi normalitas mungkin tidak akurat jika asumsi tersebut dilanggar. Interval kepercayaan yang salah dapat menyebabkan kesimpulan yang salah tentang rentang nilai yang mungkin dari koefisien regresi.
- Uji Hipotesis: Uji hipotesis (seperti uji t dan uji F) menjadi tidak valid jika residual tidak normal. Hal ini dapat menyebabkan kesalahan dalam pengambilan keputusan tentang apakah akan menolak atau menerima hipotesis nol.
- Contoh Kesalahan Tipe I dan Tipe II:
- Kesalahan Tipe I (False Positive): Jika asumsi normalitas dilanggar, kita mungkin menolak hipotesis nol (misalnya, tidak ada hubungan antara variabel) padahal sebenarnya benar. Contohnya, dalam studi tentang efektivitas obat, jika residual tidak normal, kita mungkin salah menyimpulkan bahwa obat tersebut efektif, padahal sebenarnya tidak.
- Kesalahan Tipe II (False Negative): Kita mungkin gagal menolak hipotesis nol padahal sebenarnya salah. Contohnya, dalam analisis dampak kebijakan ekonomi, jika residual tidak normal, kita mungkin salah menyimpulkan bahwa kebijakan tersebut tidak berdampak, padahal sebenarnya berdampak.
1.3. Deskripsi Sederhana Uji Normalitas
Uji normalitas adalah cara untuk memeriksa apakah data kita mengikuti pola distribusi normal, yang sering disebut sebagai “kurva lonceng”. Uji ini membandingkan data kita dengan kurva lonceng ideal. Jika data kita sangat berbeda dari kurva lonceng, maka asumsi normalitas dilanggar. Analoginya seperti mencoba mencocokkan bentuk awan dengan bentuk lonceng; jika awan terlihat seperti lonceng, data kita mungkin normal; jika tidak, data kita mungkin tidak normal.
1.4. Ilustrasi Deskriptif Distribusi, Cara mengatasi uji normalitas eviews
Perbedaan antara distribusi normal dan non-normal sangat penting untuk dipahami. Berikut adalah ilustrasi deskriptif dari kedua jenis distribusi tersebut:
Normal: Distribusi simetris, berbentuk lonceng. Mean, median, dan modus berhimpit. Sebagian besar data terkonsentrasi di sekitar mean.
Non-Normal: Distribusi dapat berbentuk asimetris (skewed) atau memiliki kurtosis yang tinggi (leptokurtic) atau rendah (platykurtic). Mean, median, dan modus tidak berhimpit. Data tersebar tidak merata.
- Skewness Positif: Ekor distribusi memanjang ke kanan. Mean lebih besar dari median. Contohnya, distribusi pendapatan di mana sebagian kecil orang memiliki pendapatan yang sangat tinggi.
- Skewness Negatif: Ekor distribusi memanjang ke kiri. Mean lebih kecil dari median. Contohnya, distribusi nilai ujian yang banyak siswa mendapat nilai tinggi.
- Kurtosis Tinggi (Leptokurtic): Distribusi memiliki puncak yang lebih tinggi dan ekor yang lebih berat dibandingkan distribusi normal. Data terkonsentrasi di sekitar mean, tetapi ada juga outlier yang signifikan. Contohnya, data harga saham yang fluktuatif.
- Kurtosis Rendah (Platykurtic): Distribusi memiliki puncak yang lebih rendah dan ekor yang lebih ringan dibandingkan distribusi normal. Data tersebar lebih merata. Contohnya, data nilai ujian yang sangat beragam.
| Karakteristik | Distribusi Normal | Distribusi Non-Normal |
|---|---|---|
| Bentuk Distribusi | Simetris, berbentuk lonceng | Asimetris (skewed), atau memiliki kurtosis tinggi/rendah |
| Ukuran Pusat | Mean = Median = Modus | Mean ≠ Median ≠ Modus |
| Ukuran Penyebaran | Standar Deviasi (relatif kecil) | Standar Deviasi (lebih besar atau bervariasi) |
| Contoh Visual | Kurva lonceng yang simetris | Kurva skewed (condong) ke kiri/kanan, atau kurva dengan puncak tinggi/rendah |
Penting untuk selalu menginterpretasikan hasil uji normalitas dengan hati-hati. Jika asumsi normalitas dilanggar, ada beberapa cara untuk mengatasinya, seperti transformasi data atau menggunakan metode regresi yang lebih robust.
Metode Uji Normalitas di EViews: Cara Mengatasi Uji Normalitas Eviews
Uji normalitas adalah langkah krusial dalam analisis data, terutama dalam konteks regresi. Tujuannya adalah untuk memastikan bahwa residual (selisih antara nilai observasi dan nilai yang diprediksi) terdistribusi secara normal. Asumsi normalitas ini penting karena banyak pengujian statistik, seperti uji-t dan uji-F, mengasumsikan normalitas residual. Pelanggaran asumsi normalitas dapat menghasilkan kesimpulan yang tidak akurat. EViews menyediakan berbagai metode untuk menguji normalitas, memungkinkan peneliti untuk memilih metode yang paling sesuai dengan karakteristik data mereka.
Mengatasi uji normalitas di EViews seringkali menantang, namun sama seperti ketika kita dihadapkan pada masalah teknis, misalnya headset Bluetooth yang tiba-tiba mati sebelah kiri. Jika Anda mengalami masalah tersebut, jangan panik, coba ikuti panduan di cara memperbaiki headset bluetooth mati sebelah kiri. Sama halnya dengan mengatasi data yang tidak normal, kita perlu melakukan transformasi data atau memilih model yang lebih sesuai.
Intinya, baik dalam dunia statistik maupun teknologi, pendekatan yang sistematis dan kesabaran adalah kunci.
Metode Uji Normalitas yang Tersedia di EViews
EViews menawarkan beberapa metode uji normalitas yang umum digunakan. Setiap metode memiliki pendekatan yang berbeda dalam mengevaluasi distribusi data terhadap distribusi normal. Memahami perbedaan antara metode-metode ini penting untuk memilih uji yang paling tepat dan menginterpretasikan hasilnya secara akurat.
- Uji Jarque-Bera: Uji ini adalah uji yang paling sering digunakan. Jarque-Bera menguji normalitas berdasarkan skewness (kecondongan) dan kurtosis (keruncingan) dari data. Hipotesis nol (H0) adalah bahwa data terdistribusi secara normal. Jika nilai statistik Jarque-Bera signifikan (p-value < tingkat signifikansi, misalnya 0.05), maka H0 ditolak, yang menunjukkan bahwa data tidak terdistribusi secara normal.
- Uji Shapiro-Wilk: Uji ini lebih kuat, terutama untuk sampel kecil (n < 50). Shapiro-Wilk menguji normalitas dengan membandingkan statistik uji yang dihitung dari data sampel dengan nilai yang diharapkan dari distribusi normal. Hipotesis nol (H0) adalah bahwa data terdistribusi secara normal. Penolakan H0 menunjukkan bahwa data tidak normal.
- Uji Kolmogorov-Smirnov: Uji ini membandingkan fungsi distribusi kumulatif (CDF) dari data sampel dengan CDF dari distribusi normal. Uji ini lebih sensitif terhadap penyimpangan pada ekor distribusi. Hipotesis nol (H0) adalah bahwa data terdistribusi secara normal. Penolakan H0 mengindikasikan bahwa data tidak normal.
Langkah-langkah Detail Melakukan Uji Normalitas Jarque-Bera di EViews
Uji Jarque-Bera adalah metode yang paling sering digunakan untuk menguji normalitas dalam EViews. Berikut adalah langkah-langkah detail untuk melakukan uji Jarque-Bera pada residual dalam EViews.
Mengatasi uji normalitas di EViews memang krusial untuk memastikan hasil analisis yang valid. Tapi, pernahkah terpikir bagaimana memanfaatkan kreativitas dalam situasi lain? Misalnya, saat membutuhkan perlindungan darurat, ide membuat rompi dari koran bisa jadi solusi, bahkan ada panduan lengkapnya di cara membuat rompi dari koran. Kembali ke EViews, pemahaman mendalam tentang metode transformasi data atau pemilihan model alternatif adalah kunci untuk melewati tantangan uji normalitas dan mendapatkan kesimpulan yang akurat.
- Peroleh Residual: Lakukan analisis regresi dalam EViews. Setelah regresi selesai, residual akan secara otomatis tersimpan dalam objek residual. Jika belum tersimpan, buat variabel residual secara manual dengan rumus `resid = y – yhat`, dimana `y` adalah variabel dependen dan `yhat` adalah nilai yang diprediksi.
- Buka Residual: Klik ganda pada variabel residual di jendela workfile EViews.
- Buka Menu View: Di jendela residual, pilih menu “View”.
- Pilih Test for Normality: Di dalam menu “View”, pilih “Descriptive Statistics & Tests” lalu pilih “Histogram and Stats”.
- Interpretasi Hasil: EViews akan menampilkan output dengan beberapa statistik, termasuk statistik Jarque-Bera, p-value, skewness, dan kurtosis. Perhatikan p-value dari uji Jarque-Bera. Jika p-value kurang dari tingkat signifikansi (misalnya, 0.05), tolak hipotesis nol (H0) yang menyatakan bahwa residual terdistribusi secara normal. Ini berarti residual tidak terdistribusi secara normal.
Perbandingan Kelebihan dan Kekurangan Metode Uji Normalitas di EViews
Setiap metode uji normalitas memiliki kelebihan dan kekurangan. Pemilihan metode yang tepat bergantung pada ukuran sampel, karakteristik data, dan tingkat sensitivitas yang diinginkan. Memahami aspek-aspek ini memungkinkan peneliti untuk membuat keputusan yang lebih tepat.
- Jarque-Bera:
- Kelebihan: Mudah diinterpretasi, secara luas digunakan, memberikan informasi tentang skewness dan kurtosis.
- Kekurangan: Kurang sensitif untuk sampel kecil, mungkin kurang akurat jika data memiliki outlier ekstrem.
- Shapiro-Wilk:
- Kelebihan: Lebih kuat untuk sampel kecil, sensitif terhadap berbagai jenis penyimpangan dari normalitas.
- Kekurangan: Tidak tersedia untuk sampel yang sangat besar, kurang intuitif dibandingkan Jarque-Bera.
- Kolmogorov-Smirnov:
- Kelebihan: Relatif mudah dihitung, dapat digunakan untuk membandingkan distribusi data dengan distribusi lain selain normal.
- Kekurangan: Kurang kuat dibandingkan Shapiro-Wilk, terutama untuk sampel kecil.
Tabel Perbandingan Metode Uji Normalitas
Berikut adalah tabel yang merangkum perbandingan antara metode uji normalitas yang umum digunakan di EViews.
| Metode Uji | Statistik Uji | Interpretasi | Batasan |
|---|---|---|---|
| Jarque-Bera | JB = n[S^2/6 + (K-3)^2/24] | Hipotesis nol (H0): Data terdistribusi normal. Tolak H0 jika p-value < tingkat signifikansi. | Kurang sensitif untuk sampel kecil, rentan terhadap outlier. |
| Shapiro-Wilk | W = (∑ai xi)^2 / ∑(xi – x̄)^2 | Hipotesis nol (H0): Data terdistribusi normal. Tolak H0 jika p-value < tingkat signifikansi. | Tidak tersedia untuk sampel yang sangat besar. |
| Kolmogorov-Smirnov | D = max|F(x)
Oke, mari kita bedah. Saat berhadapan dengan uji normalitas di EViews, seringkali kita perlu melakukan transformasi data atau menggunakan metode lain untuk memastikan data kita terdistribusi normal. Tapi, pernahkah terpikir, seberapa lama data yang kita gunakan itu ‘berumur’? Analoginya seperti kita ingin tahu cara mengetahui umur kartu Indosat , agar kita tahu ‘umur’ data kita dan bagaimana ia bisa mempengaruhi hasil analisis. Kembali ke EViews, mengatasi masalah normalitas seringkali membutuhkan kreativitas dan pemahaman mendalam tentang data yang kita miliki.
|
Hipotesis nol (H0): Data terdistribusi normal. Tolak H0 jika p-value < tingkat signifikansi. | Kurang kuat dibandingkan Shapiro-Wilk, terutama untuk sampel kecil. |
Interpretasi Hasil Uji Normalitas
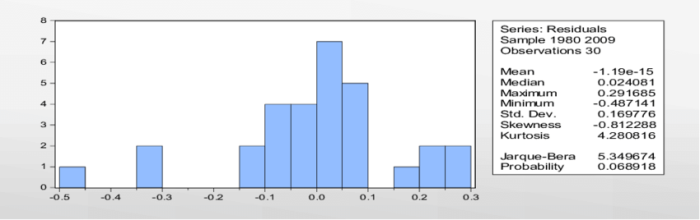
Source: identif.id
Menghadapi uji normalitas di Eviews memang menantang, seringkali data kita tidak langsung memenuhi asumsi. Tapi, sebelum panik, mari kita selesaikan langkah demi langkah. Saya teringat, ketika saya pertama kali membuat jurnal kelas, prosesnya juga terasa rumit, sama seperti ketika kita berhadapan dengan data yang tidak normal. Untungnya, ada panduan praktis seperti cara membuat jurnal kelas yang sangat membantu.
Nah, setelah kita memahami dasar-dasar, kita bisa kembali fokus pada Eviews, mencari solusi transformasinya, atau memilih metode yang lebih robust terhadap pelanggaran asumsi normalitas.
Setelah melakukan uji normalitas menggunakan EViews, langkah selanjutnya adalah menginterpretasi hasil output yang dihasilkan. Interpretasi yang tepat sangat krusial untuk menentukan apakah data yang dianalisis terdistribusi secara normal atau tidak. Keputusan ini akan memengaruhi pemilihan metode analisis statistik yang tepat dan validitas kesimpulan yang ditarik.
Memahami Output Uji Normalitas EViews
Output uji normalitas EViews umumnya menyajikan beberapa informasi penting. Informasi tersebut meliputi statistik uji, nilai p-value, dan keputusan mengenai normalitas data. Memahami masing-masing elemen ini adalah kunci untuk interpretasi yang akurat.
- Statistik Uji: EViews menyediakan berbagai statistik uji normalitas, yang paling umum adalah Jarque-Bera. Statistik ini mengukur seberapa jauh distribusi data dari distribusi normal. Nilai statistik uji yang lebih besar menunjukkan penyimpangan yang lebih besar dari normalitas.
- P-value: Nilai p-value adalah probabilitas untuk mendapatkan hasil uji statistik yang sama atau lebih ekstrem, dengan asumsi bahwa hipotesis nol (data terdistribusi normal) benar.
- Keputusan: Berdasarkan nilai p-value, kita membuat keputusan apakah akan menolak atau menerima hipotesis nol. Jika p-value lebih kecil dari tingkat signifikansi (misalnya, 0.05), kita menolak hipotesis nol dan menyimpulkan bahwa data tidak terdistribusi secara normal. Sebaliknya, jika p-value lebih besar dari tingkat signifikansi, kita gagal menolak hipotesis nol dan menyimpulkan bahwa data terdistribusi secara normal.
Interpretasi Contoh Hasil Uji Jarque-Bera
Interpretasi hasil uji Jarque-Bera sangat bergantung pada nilai p-value yang dihasilkan. Berikut adalah contoh konkret dengan nilai p-value yang berbeda:
- Contoh 1: P-value Signifikan (P-value < 0.05)
Misalkan output EViews menunjukkan nilai Jarque-Bera sebesar 5.25 dan p-value sebesar 0.02. Karena p-value (0.02) lebih kecil dari tingkat signifikansi 0.05, kita menolak hipotesis nol. Ini berarti data tidak terdistribusi secara normal. Implikasinya, penggunaan metode statistik yang mengasumsikan normalitas data mungkin tidak tepat.
Menghadapi uji normalitas di EViews memang butuh strategi jitu, mulai dari transformasi data hingga memilih metode yang tepat. Tapi, pernahkah Anda membayangkan betapa presisinya perhitungan sudut pada jam analog? Sama halnya dengan ketelitian dalam mengolah data, untuk mengetahui sudut yang dibentuk jarum jam, kita perlu rumus yang tepat. Jika Anda tertarik dengan cara menghitungnya, simak penjelasannya di cara menghitung sudut dengan jarum jam.
Kembali ke EViews, memahami distribusi data adalah kunci untuk mengatasi masalah non-normalitas, sehingga model yang kita hasilkan lebih akurat.
- Contoh 2: P-value Tidak Signifikan (P-value > 0.05)
Misalkan output EViews menunjukkan nilai Jarque-Bera sebesar 1.10 dan p-value sebesar 0.25. Karena p-value (0.25) lebih besar dari tingkat signifikansi 0.05, kita gagal menolak hipotesis nol. Ini berarti data terdistribusi secara normal. Dengan demikian, metode statistik yang mengasumsikan normalitas data dapat digunakan.
Menentukan Normalitas Data Berdasarkan Output EViews
Untuk menentukan apakah data terdistribusi secara normal, perhatikan langkah-langkah berikut:
- Perhatikan Statistik Uji: Meskipun penting, statistik uji (misalnya, Jarque-Bera) sendiri tidak memberikan kesimpulan akhir. Nilai statistik uji hanya memberikan gambaran awal mengenai seberapa jauh data menyimpang dari normalitas.
- Periksa P-value: Ini adalah elemen paling penting dalam interpretasi. Bandingkan p-value dengan tingkat signifikansi yang telah ditetapkan (biasanya 0.05).
- Ambil Keputusan:
- Jika p-value ≤ tingkat signifikansi, tolak hipotesis nol. Data tidak terdistribusi secara normal.
- Jika p-value > tingkat signifikansi, gagal menolak hipotesis nol. Data terdistribusi secara normal.
Ilustrasi Output Uji Normalitas EViews
Berikut adalah ilustrasi contoh output uji normalitas dari EViews. Perhatikan bagian-bagian yang paling relevan untuk interpretasi:
Contoh Output:
Test for Normality -------------------- Jarque-Bera 5.250000 Probability 0.020000 <-- P-value
Penjelasan Ilustrasi:
- “Jarque-Bera”: Menunjukkan nilai statistik uji Jarque-Bera.
- “Probability”: Menunjukkan nilai p-value.
- Interpretasi: Dalam contoh ini, p-value (0.02) lebih kecil dari tingkat signifikansi 0.05. Oleh karena itu, data tidak terdistribusi secara normal.
Terakhir
Melalui pembahasan ini, kita telah menjelajahi seluk-beluk uji normalitas dalam EViews, mulai dari pentingnya asumsi normalitas hingga metode praktis untuk mengatasinya. Pemahaman mendalam tentang konsep ini, beserta interpretasi yang tepat, adalah kunci untuk menghasilkan analisis regresi yang akurat dan bermakna. Ingatlah, uji normalitas bukanlah sekadar formalitas, melainkan landasan untuk memastikan validitas kesimpulan Anda. Dengan pengetahuan dan alat yang tepat, Anda dapat mengatasi tantangan ini dan menghasilkan analisis yang lebih kuat dan terpercaya.
FAQ dan Informasi Bermanfaat
Apa itu uji normalitas?
Uji normalitas adalah metode statistik untuk menentukan apakah data sampel memiliki distribusi yang mendekati distribusi normal (lonceng).
Mengapa uji normalitas penting dalam analisis regresi?
Uji normalitas memastikan bahwa asumsi klasik regresi terpenuhi, yang mempengaruhi validitas nilai p, standar error, dan uji hipotesis.
Metode uji normalitas apa saja yang umum digunakan di EViews?
Beberapa metode uji normalitas yang umum digunakan di EViews meliputi Jarque-Bera, Shapiro-Wilk, dan Kolmogorov-Smirnov.
Apa yang harus dilakukan jika data tidak normal?
Jika data tidak normal, pertimbangkan transformasi data (seperti Box-Cox atau logaritma) atau gunakan metode non-parametrik.
Bagaimana cara menginterpretasi hasil uji Jarque-Bera di EViews?
Perhatikan nilai p-value. Jika p-value tingkat signifikansi, data dianggap normal.












