Cara Mengerjakan Luas Segitiga Panduan Lengkap dan Penerapannya

Siap untuk mengungkap rahasia di balik cara mengerjakan luas segitiga? Jangan salah, ini bukan sekadar rumus matematika. Ini adalah kunci untuk membuka dunia geometri, arsitektur, desain, dan bahkan navigasi. Memahami konsep dasar luas segitiga adalah seperti memiliki peta harta karun yang akan memandu dalam memecahkan berbagai masalah praktis.

Dalam panduan ini, akan dijelajahi mengapa pemahaman mendalam tentang luas segitiga sangat penting, bagaimana rumus tersebut diturunkan, dan strategi efektif untuk mengidentifikasi serta mengukur elemen-elemen penting pada segitiga. Akan dibahas juga penerapan konsep luas segitiga dalam pemecahan masalah yang lebih kompleks, dari merancang taman hingga menganalisis data. Bersiaplah untuk mengubah cara memandang segitiga dan membuka potensi tak terbatasnya!

Mengapa Pemahaman Konsep Dasar Luas Segitiga Membuka Pintu Kemudahan dalam Menyelesaikan Berbagai Soal Geometri

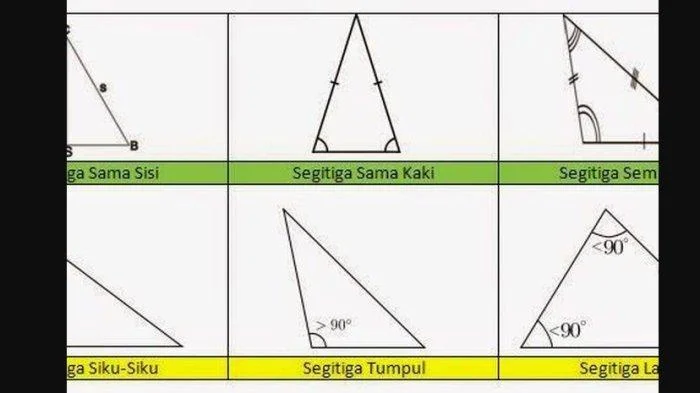
Memahami konsep dasar luas segitiga adalah fondasi krusial dalam dunia geometri. Ini bukan hanya tentang menghitung angka; tetapi tentang membangun kerangka berpikir yang kuat untuk memahami bentuk, ruang, dan hubungan antar bangun datar. Dengan menguasai konsep ini, kita membuka pintu menuju pemahaman yang lebih dalam tentang berbagai konsep geometri lainnya, serta kemampuan untuk memecahkan masalah praktis dalam kehidupan sehari-hari.

Konsep luas segitiga menjadi kunci untuk menguasai berbagai konsep geometri. Mari kita bedah lebih dalam bagaimana pemahaman ini memberikan kemudahan dalam menyelesaikan soal-soal geometri.

Fondasi Geometri dan Penerapan Luas Segitiga

Konsep dasar luas segitiga adalah landasan penting dalam memahami geometri. Pemahaman ini melampaui sekadar menghitung luas; ini adalah tentang mengembangkan kemampuan visualisasi spasial dan kemampuan untuk memecah bangun kompleks menjadi bagian-bagian yang lebih sederhana. Ini sangat penting karena banyak bangun datar lainnya, seperti persegi panjang, belah ketupat, trapesium, dan bahkan bangun ruang seperti prisma dan limas, dapat dipecah atau dibangun dari segitiga.

Sebagai contoh, luas persegi panjang dapat dipandang sebagai gabungan dari dua segitiga siku-siku yang identik. Luas trapesium dapat dihitung dengan membaginya menjadi sebuah persegi panjang dan dua segitiga. Bahkan, perhitungan volume bangun ruang seringkali melibatkan perhitungan luas alas yang berbentuk segitiga, seperti pada limas. Dengan demikian, pemahaman yang kuat tentang luas segitiga memungkinkan kita untuk:

• Menghitung luas bangun datar kompleks dengan membaginya menjadi segitiga-segitiga yang lebih mudah dihitung.
• Memahami hubungan antara berbagai bangun datar dan bangun ruang, serta bagaimana mereka saling terkait.
• Mengembangkan kemampuan untuk memecahkan masalah geometri yang lebih kompleks dengan lebih mudah.

Manfaat pemahaman konsep luas segitiga juga sangat terasa dalam memecahkan masalah sehari-hari. Misalnya, ketika menghitung luas tanah yang berbentuk tidak beraturan, kita dapat membaginya menjadi segitiga-segitiga dan menghitung luasnya masing-masing, kemudian menjumlahkannya. Dalam proyek konstruksi sederhana, seperti membuat atap rumah berbentuk segitiga, pemahaman tentang luas segitiga memungkinkan kita untuk menghitung kebutuhan material, seperti kayu atau genteng, dengan lebih akurat. Ini juga membantu dalam mengestimasi biaya proyek secara keseluruhan.

Pemahaman ini tidak hanya relevan dalam konteks akademis, tetapi juga dalam kehidupan sehari-hari. Misalnya, ketika merencanakan tata letak ruangan, memahami luas segitiga membantu dalam mengoptimalkan penggunaan ruang dan menentukan bagaimana perabotan dapat ditempatkan secara efisien. Dalam desain grafis, konsep ini digunakan untuk membuat bentuk dan desain yang menarik secara visual. Dengan kata lain, pemahaman tentang luas segitiga adalah keterampilan dasar yang memiliki aplikasi luas dan memberikan manfaat nyata dalam berbagai aspek kehidupan.

Studi Kasus: Dampak Kesalahan Pemahaman Luas Segitiga

Kesalahan dalam memahami konsep dasar luas segitiga dapat menyebabkan kesalahan fatal dalam perhitungan yang lebih kompleks. Mari kita ambil contoh kasus nyata dalam proyek konstruksi sederhana.

Misalkan seorang kontraktor salah menghitung luas atap rumah yang berbentuk segitiga. Ia menganggap atap tersebut sebagai persegi panjang dan menghitung luasnya menggunakan rumus panjang x lebar. Akibatnya, ia memesan material atap (misalnya, genteng) yang jauh lebih sedikit dari yang dibutuhkan. Kesalahan ini berakibat pada:

• Kekurangan material, yang menyebabkan penundaan proyek dan potensi biaya tambahan untuk pengadaan material darurat.
• Ketidaksesuaian desain atap, yang dapat mengganggu estetika rumah dan bahkan menyebabkan masalah struktural.
• Kerugian finansial akibat pembelian material yang tidak mencukupi dan potensi biaya perbaikan.

Ilustrasi deskriptif:

• Ilustrasi 1: Gambar sketsa atap rumah berbentuk segitiga. Di sampingnya, terdapat perhitungan yang salah, yang mengasumsikan atap sebagai persegi panjang. Perhitungan yang benar (dengan menggunakan rumus luas segitiga) juga ditampilkan untuk perbandingan. Perbedaan luas yang signifikan menjadi jelas.
• Ilustrasi 2: Gambar visual dari kekurangan genteng pada atap yang sudah terpasang, menunjukkan celah-celah yang tidak tertutup.
• Ilustrasi 3: Gambar seorang kontraktor yang sedang kebingungan melihat kekurangan material dan berdiskusi dengan pemilik rumah.

Studi kasus ini menyoroti pentingnya pemahaman yang akurat tentang konsep luas segitiga. Kesalahan dalam perhitungan dasar dapat memiliki konsekuensi yang merugikan, baik dari segi biaya, waktu, maupun kualitas proyek.

Perbandingan Rumus Luas Segitiga

Tabel berikut membandingkan berbagai jenis segitiga dan rumus luas yang digunakan. Tabel ini juga mencakup contoh perhitungan untuk masing-masing jenis segitiga.

Memahami cara mengerjakan luas segitiga itu fundamental, kan? Rumusnya sederhana: setengah alas kali tinggi. Tapi, bagaimana memastikan siswa benar-benar paham konsep ini? Nah, di sinilah peran penting RPP , yang menjadi panduan guru dalam merancang pembelajaran yang efektif. Dengan RPP yang tepat, materi luas segitiga bisa disampaikan dengan cara yang lebih mudah dipahami, sehingga siswa bisa dengan cepat menguasai cara menghitung luas segitiga dengan akurat.

Jenis Segitiga	Rumus Luas	Keterangan	Contoh Perhitungan
Segitiga Siku-Siku	1/2 x alas x tinggi	Alas dan tinggi adalah sisi-sisi yang saling tegak lurus.	Jika alas = 6 cm dan tinggi = 8 cm, maka luas = 1/2 x 6 x 8 = 24 cm²
Segitiga Sama Kaki	1/2 x alas x tinggi	Tinggi ditarik dari titik sudut yang berhadapan dengan alas ke sisi alas.	Jika alas = 10 cm dan tinggi = 5 cm, maka luas = 1/2 x 10 x 5 = 25 cm²
Segitiga Sama Sisi	(s²√3)/4 atau 1/2 x alas x tinggi	s adalah panjang sisi segitiga. Tinggi dapat dihitung menggunakan teorema Pythagoras.	Jika sisi = 4 cm, maka luas = (4²√3)/4 ≈ 6.93 cm²
Segitiga Sembarang	1/2 x alas x tinggi atau √(s(s-a)(s-b)(s-c)) (Rumus Heron)	Tinggi ditarik dari titik sudut ke sisi alas. Rumus Heron digunakan jika tinggi tidak diketahui; s adalah setengah keliling (a+b+c)/2, a, b, dan c adalah panjang sisi segitiga.	Jika alas = 7 cm, tinggi = 6 cm, maka luas = 1/2 x 7 x 6 = 21 cm². Jika sisi a=5, b=6, c=7, maka s = (5+6+7)/2 = 9. Luas = √(9(9-5)(9-6)(9-7)) ≈ 14.7 cm²

Tabel ini memberikan gambaran komprehensif tentang rumus luas untuk berbagai jenis segitiga, memudahkan pembaca untuk memahami dan menerapkan rumus yang tepat sesuai dengan jenis segitiga yang dihadapi.

Tips Praktis untuk Memahami Rumus Luas Segitiga

Mengingat dan memahami rumus luas segitiga dapat menjadi lebih mudah dengan menggunakan beberapa strategi berikut:

• Gunakan Mnemonic: Buat mnemonic yang mudah diingat. Misalnya, “Setengah Alas Tinggi” untuk rumus 1/2 x alas x tinggi.
• Visualisasi: Gambarlah segitiga dan bayangkan bagaimana tingginya membagi segitiga menjadi dua bagian yang sama. Visualisasi membantu mengaitkan rumus dengan bentuk geometrisnya.
• Analogi Sederhana: Gunakan analogi untuk mempermudah pemahaman. Misalnya, bayangkan segitiga sebagai setengah dari persegi panjang. Ini membantu mengingat bahwa luas segitiga adalah setengah dari luas persegi panjang dengan alas dan tinggi yang sama.
• Latihan Soal: Kerjakan berbagai soal latihan untuk memperkuat pemahaman. Semakin banyak berlatih, semakin mudah untuk mengingat dan menerapkan rumus.
• Gunakan Alat Bantu: Manfaatkan alat bantu seperti kalkulator, aplikasi geometri, atau video tutorial untuk memvisualisasikan konsep dan memecahkan soal.

Dengan menerapkan tips ini, siswa dan pembaca dapat lebih mudah memahami dan mengingat rumus luas segitiga, serta meningkatkan kemampuan mereka dalam memecahkan soal geometri.

Mengungkap Rahasia Rumus Luas Segitiga

Rumus luas segitiga, 1/2
– alas
– tinggi, adalah salah satu konsep fundamental dalam geometri. Pemahaman mendalam tentang bagaimana rumus ini bekerja membuka pintu ke berbagai aplikasi praktis, mulai dari perhitungan sederhana hingga solusi masalah yang kompleks. Artikel ini akan membahas secara rinci asal-usul rumus ini, penerapannya dalam berbagai bidang, dan contoh perhitungan yang relevan.

Menurunkan Rumus Luas Segitiga: Dari Pythagoras hingga Geometri

Rumus luas segitiga, 1/2
– alas
– tinggi, bukanlah sekadar formula ajaib. Penurunannya didasarkan pada prinsip-prinsip geometri yang kokoh. Untuk memahami asal-usulnya, kita perlu menelusuri kembali ke dasar-dasar geometri dan memahami hubungan antara segitiga dan bangun datar lainnya, seperti persegi panjang.

Berikut adalah langkah-langkah untuk menurunkan rumus luas segitiga:

• Hubungan dengan Persegi Panjang: Bayangkan sebuah persegi panjang. Luasnya mudah dihitung: panjang
  – lebar. Sekarang, bagi persegi panjang tersebut menjadi dua segitiga yang identik dengan menarik garis diagonal. Setiap segitiga yang terbentuk memiliki alas yang sama dengan panjang persegi panjang dan tinggi yang sama dengan lebar persegi panjang.
• Luas Segitiga: Karena persegi panjang dibagi menjadi dua segitiga yang sama besar, maka luas setiap segitiga adalah setengah dari luas persegi panjang. Dengan demikian, luas segitiga = 1/2
  – panjang
  – lebar. Dalam konteks segitiga, panjang disebut alas (a) dan lebar disebut tinggi (t).
• Teorema Pythagoras (Singgungan): Teorema Pythagoras (a² + b² = c²) sangat berguna untuk menghitung tinggi segitiga jika alas dan sisi miring diketahui. Teorema ini berlaku untuk segitiga siku-siku, di mana sisi miring adalah sisi terpanjang. Jika kita memiliki segitiga tumpul atau lancip, kita bisa membagi segitiga tersebut menjadi dua segitiga siku-siku untuk memanfaatkan teorema ini.
• Ilustrasi Deskriptif: Bayangkan sebuah persegi panjang dengan panjang 10 cm dan lebar 6 cm. Luasnya adalah 60 cm². Jika kita membagi persegi panjang ini menjadi dua segitiga, setiap segitiga akan memiliki luas 30 cm² (1/2
  – 10 cm
  – 6 cm). Perhatikan bagaimana alas dan tinggi segitiga sesuai dengan panjang dan lebar persegi panjang.

Dengan demikian, rumus luas segitiga (1/2
– alas
– tinggi) diturunkan secara logis dari hubungan antara segitiga dan persegi panjang, serta prinsip-prinsip dasar geometri.

Memahami cara menghitung luas segitiga memang krusial, mulai dari rumus dasar hingga variasi berdasarkan jenis segitiga. Namun, sebelum masuk lebih dalam, penting untuk mengidentifikasi jenis segitiga yang kamu hadapi. Nah, untuk memudahkan proses identifikasi ini, kamu bisa memanfaatkan platform seperti Identif , yang bisa membantumu mengenali bentuk-bentuk geometri dengan cepat. Dengan begitu, perhitungan luas segitiga akan jadi lebih mudah dan akurat, karena kamu sudah tahu rumus mana yang tepat digunakan.

Contoh Perhitungan Kompleks: Segitiga Tumpul dan Trigonometri

Mari kita hadapi tantangan: menghitung luas segitiga tumpul. Dalam kasus ini, tinggi tidak langsung terlihat. Kita perlu menggunakan konsep trigonometri atau teorema lainnya untuk menemukan tinggi.

Kasus: Misalkan kita memiliki segitiga tumpul dengan sisi-sisi 8 cm, 10 cm, dan sudut tumpul sebesar 150 derajat. Kita akan menggunakan aturan sinus dan kosinus untuk menemukan tinggi.

1. Menemukan Tinggi:
   • Gunakan aturan sinus untuk menemukan sudut lain.
   • Gunakan aturan kosinus untuk menemukan sisi yang berlawanan dengan sudut tumpul.
   • Setelah menemukan sisi yang berlawanan, gunakan fungsi sinus untuk menghitung tinggi. Tinggi akan menjadi sisi yang berlawanan dikalikan dengan sinus sudut yang berdekatan dengan alas.
2. Perhitungan:
   • Misalkan alas segitiga adalah sisi dengan panjang 8 cm.
   • Gunakan aturan kosinus: c² = a² + b²
     -2ab
     – cos(C), di mana C adalah sudut tumpul (150 derajat).
   • Hitung panjang sisi yang berlawanan dengan sudut tumpul.
   • Gunakan fungsi sinus untuk menemukan tinggi (t): t = sisi yang berlawanan
     – sin(30 derajat).
3. Luas: Setelah tinggi ditemukan, gunakan rumus luas segitiga: 1/2
   • alas
   • tinggi.

Contoh ini menunjukkan bahwa bahkan untuk segitiga yang tampak rumit, kita dapat menggunakan alat matematika yang tepat untuk menemukan luasnya.

Memahami luas segitiga itu krusial, rumusnya sederhana: 1/2 alas tinggi. Tapi, bagaimana cara mengajar konsep ini secara efektif di kelas? Jawabannya bisa ditemukan dalam Panduan Lengkap RPP MTS Kurikulum Merdeka. Di sana, Anda akan menemukan strategi pembelajaran yang terstruktur dan mudah diikuti, yang akan sangat membantu dalam menjelaskan konsep luas segitiga kepada siswa Anda. Dengan begitu, siswa akan lebih mudah memahami dan menguasai cara menghitung luas segitiga.

Penerapan Luas Segitiga dalam Berbagai Bidang

Rumus luas segitiga memiliki aplikasi yang luas di berbagai bidang, menjadikannya alat yang sangat berguna bagi para profesional.

• Arsitektur: Arsitek menggunakan rumus luas segitiga untuk menghitung luas atap berbentuk segitiga, dinding miring, dan elemen desain lainnya. Perhitungan yang akurat sangat penting untuk perencanaan material dan biaya konstruksi.
• Desain Grafis: Desainer grafis menggunakan rumus luas segitiga untuk menghitung area dalam bentuk segitiga yang digunakan dalam logo, ilustrasi, dan desain lainnya. Ini membantu dalam penentuan ukuran, penempatan, dan proporsi elemen desain.
• Navigasi: Dalam navigasi, khususnya triangulasi, rumus luas segitiga digunakan untuk menghitung jarak. Dengan mengukur sudut dan jarak antara titik-titik referensi, kita dapat menggunakan rumus luas segitiga untuk menentukan posisi dan jarak ke lokasi lain.
• Surveying: Surveyor menggunakan prinsip-prinsip geometri, termasuk perhitungan luas segitiga, untuk memetakan dan mengukur lahan. Ini sangat penting untuk perencanaan kota, konstruksi, dan penentuan batas properti.

Kutipan dari Tokoh Terkenal

“Pemahaman mendalam tentang konsep luas segitiga adalah fondasi penting dalam geometri dan berbagai aplikasi praktis. Kemampuan untuk menghitung luas segitiga secara akurat adalah kunci untuk memecahkan masalah di banyak bidang, mulai dari arsitektur hingga navigasi.”
– Leonardo da Vinci (ilustrasi yang relevan dengan bidang yang disebutkan di atas)

Strategi Efektif dalam Mengidentifikasi dan Mengukur Unsur-Unsur Penting pada Segitiga untuk Menghitung Luasnya: Cara Mengerjakan Luas Segitiga

Memahami cara menghitung luas segitiga adalah keterampilan dasar dalam geometri. Namun, keberhasilan dalam menghitung luas tidak hanya bergantung pada penggunaan rumus yang tepat, tetapi juga pada kemampuan untuk mengidentifikasi dan mengukur unsur-unsur penting segitiga dengan akurat. Artikel ini akan memandu Anda melalui strategi efektif untuk mengidentifikasi alas dan tinggi, serta memberikan tips untuk menghindari kesalahan umum dalam pengukuran dan perhitungan.

Mengidentifikasi dan Mengukur Alas dan Tinggi Segitiga dengan Presisi, Cara mengerjakan luas segitiga

Langkah pertama dalam menghitung luas segitiga adalah mengidentifikasi alas dan tinggi. Alas adalah sisi mana pun dari segitiga yang dipilih sebagai dasar, sedangkan tinggi adalah jarak tegak lurus dari alas ke titik sudut yang berlawanan. Pengukuran yang akurat sangat penting untuk mendapatkan hasil yang benar. Berikut adalah langkah-langkah detail untuk memastikan pengukuran yang tepat:

• Memilih Alas: Pilih sisi yang paling mudah diukur atau yang paling sesuai dengan informasi yang diberikan dalam soal. Pada segitiga sembarang, Anda bebas memilih sisi mana saja sebagai alas.
• Menentukan Tinggi: Tinggi harus diukur tegak lurus dari alas ke titik sudut yang berlawanan. Gunakan penggaris atau meteran untuk mengukur jarak ini. Pastikan pengukuran dilakukan pada sudut 90 derajat terhadap alas.
• Menggunakan Alat Ukur yang Tepat:
  • Penggaris: Cocok untuk segitiga kecil atau pengukuran di atas kertas. Pastikan penggaris ditempatkan sejajar dengan alas dan tinggi diukur secara tegak lurus.
  • Meteran: Ideal untuk segitiga yang lebih besar atau pengukuran di lapangan. Pastikan meteran ditarik lurus dan tegak lurus terhadap alas.
• Teknik Pengukuran yang Akurat:
  • Mata Sejajar: Pastikan mata Anda sejajar dengan skala alat ukur untuk menghindari kesalahan paralaks.
  • Pembacaan yang Tepat: Baca skala alat ukur dengan cermat, perhatikan satuan yang digunakan (cm, mm, m, dll.).

Perbedaan pengukuran pada berbagai jenis segitiga memerlukan pendekatan yang berbeda:

• Segitiga Siku-Siku: Salah satu sisi segitiga siku-siku adalah tinggi jika sisi lainnya adalah alas. Tinggi dan alas saling tegak lurus.
• Segitiga Sama Kaki: Tinggi ditarik dari titik sudut yang berlawanan dengan sisi yang tidak sama (alas) ke tengah alas.
• Segitiga Sama Sisi: Tinggi ditarik dari salah satu titik sudut ke tengah sisi yang berlawanan. Karena semua sisi sama, Anda bisa memilih sisi mana saja sebagai alas.
• Segitiga Tumpul: Tinggi mungkin berada di luar segitiga. Perpanjang alas, lalu ukur tinggi dari titik sudut yang berlawanan ke perpanjangan alas.

Dengan mengikuti langkah-langkah ini dan memahami perbedaan pengukuran pada berbagai jenis segitiga, Anda dapat memastikan pengukuran yang akurat dan perhitungan luas yang tepat.

Contoh Soal yang Menantang dan Solusinya

Terkadang, informasi tentang alas dan tinggi tidak langsung diberikan. Dalam kasus seperti itu, Anda perlu menggunakan pengetahuan tentang sifat-sifat segitiga dan rumus-rumus tambahan untuk menemukan informasi yang dibutuhkan. Berikut adalah contoh soal yang menantang beserta solusinya:

Soal: Sebuah segitiga memiliki sisi-sisi dengan panjang 13 cm, 14 cm, dan 15 cm. Hitung luas segitiga tersebut.

Solusi: Karena kita tidak memiliki informasi langsung tentang tinggi, kita akan menggunakan rumus Heron untuk menghitung luasnya. Rumus Heron adalah:

Luas = √(s(s-a)(s-b)(s-c))

Di mana:

• a, b, dan c adalah panjang sisi-sisi segitiga.
• s adalah setengah keliling segitiga, dihitung sebagai s = (a + b + c) / 2

Langkah-langkah:

1. Hitung setengah keliling (s): s = (13 + 14 + 15) / 2 = 21 cm
2. Gunakan rumus Heron: Luas = √(21(21-13)(21-14)(21-15))
3. Sederhanakan: Luas = √(21
   • 8
   • 7
   • 6) = √(7056)
4. Hitung luas: Luas ≈ 84 cm²

Dengan demikian, luas segitiga tersebut adalah sekitar 84 cm².

Panduan Visual: Mengukur Alas dan Tinggi pada Berbagai Orientasi

Mengidentifikasi alas dan tinggi dapat menjadi lebih mudah dengan panduan visual. Ilustrasi berikut menunjukkan cara mengukur alas dan tinggi pada berbagai orientasi segitiga:

Ilustrasi 1: Segitiga dengan Orientasi Standar

Deskripsi: Sebuah segitiga lancip dengan alas horizontal. Garis putus-putus tegak lurus dari titik sudut atas ke alas menunjukkan tinggi. Penggaris diletakkan di sepanjang alas dan tinggi untuk pengukuran.

Ilustrasi 2: Segitiga “Terbalik”

Memahami cara menghitung luas segitiga itu fundamental, kan? Rumusnya sederhana: 1/2 alas tinggi. Tapi, pernahkah kamu merasa kesulitan saat mengelola informasi di ponselmu? Sama seperti kamu perlu menyederhanakan perhitungan, terkadang kamu perlu membersihkan daftar kontakmu. Jika kamu merasa kewalahan dengan banyaknya kontak yang tidak perlu, pelajari cara hapus kontak di google untuk mempermudah.

Setelah itu, kamu bisa kembali fokus pada soal-soal geometri dan menghitung luas segitiga dengan lebih efisien!

Deskripsi: Segitiga lancip yang “terbalik”, dengan titik sudut di bawah. Alas berada di atas. Garis putus-putus tegak lurus dari titik sudut bawah ke alas (yang berada di atas) menunjukkan tinggi. Penggaris diletakkan di sepanjang alas dan tinggi.

Ilustrasi 3: Segitiga Miring

Deskripsi: Segitiga miring dengan alas yang tidak horizontal atau vertikal. Garis putus-putus tegak lurus dari titik sudut ke alas menunjukkan tinggi. Penggaris diletakkan untuk mengukur alas dan tinggi, dengan perhatian khusus pada sudut 90 derajat.

Ilustrasi 4: Segitiga Tumpul

Deskripsi: Segitiga tumpul. Alas diperpanjang dengan garis putus-putus. Garis putus-putus tegak lurus dari titik sudut tumpul ke perpanjangan alas menunjukkan tinggi. Penggaris digunakan untuk mengukur alas (yang diperpanjang) dan tinggi.

Memahami cara menghitung luas segitiga adalah dasar yang penting dalam matematika. Rumusnya sederhana: 1/2 alas tinggi. Namun, lebih dari sekadar rumus, belajar ini membuka gerbang ke pemahaman konsep yang lebih kompleks. Hal ini selaras dengan pentingnya Pendidikan secara keseluruhan, yang tak hanya memberikan pengetahuan, tapi juga kemampuan berpikir kritis. Pada akhirnya, dengan menguasai cara menghitung luas segitiga, kita melatih logika berpikir yang esensial dalam berbagai aspek kehidupan.

Tips untuk Menghindari Kesalahan Umum

Beberapa kesalahan umum dapat mengganggu perhitungan luas segitiga. Berikut adalah tips untuk menghindarinya:

• Identifikasi Alas dan Tinggi yang Tepat: Pastikan tinggi diukur tegak lurus terhadap alas. Jangan salah mengira sisi miring sebagai tinggi.
• Perhatikan Satuan: Pastikan semua pengukuran menggunakan satuan yang sama (misalnya, cm, m, inci). Konversikan satuan jika perlu sebelum melakukan perhitungan.
• Gunakan Rumus yang Benar: Rumus luas segitiga adalah 1/2
  – alas
  – tinggi. Pastikan Anda menggunakan rumus yang benar.
• Periksa Kembali Perhitungan: Setelah menghitung, periksa kembali pekerjaan Anda untuk memastikan tidak ada kesalahan aritmatika. Gunakan kalkulator untuk memverifikasi.
• Visualisasikan: Gambarlah segitiga dan tandai alas dan tinggi untuk membantu visualisasi dan menghindari kesalahan.

Dengan mengikuti tips ini, Anda dapat meminimalkan kesalahan dan meningkatkan akurasi perhitungan luas segitiga.

Eksplorasi Lebih Lanjut: Penerapan Konsep Luas Segitiga dalam Pemecahan Masalah yang Lebih Kompleks

Memahami luas segitiga bukan hanya tentang menghitung area; ini adalah fondasi untuk menjelajahi dunia geometri yang lebih luas. Konsep dasar ini membuka pintu ke pemahaman yang lebih mendalam tentang bentuk tiga dimensi, perhitungan volume, dan bahkan aplikasi praktis dalam desain dan analisis data. Dengan menguasai konsep dasar luas segitiga, kita dapat membangun fondasi yang kuat untuk menyelesaikan masalah geometri yang lebih kompleks dan mengembangkan kemampuan berpikir spasial yang kritis.

Pemahaman yang mendalam tentang luas segitiga memungkinkan kita untuk merambah ke berbagai konsep geometri yang lebih maju. Konsep ini berfungsi sebagai batu loncatan untuk memahami volume prisma, luas permukaan bangun ruang, dan bahkan perhitungan jarak dalam ruang tiga dimensi. Mari kita uraikan bagaimana konsep-konsep ini saling terkait dan bagaimana luas segitiga berperan sebagai landasan penting.

Konsep Luas Segitiga sebagai Dasar Konsep Geometri Lanjutan

Luas segitiga memainkan peran krusial dalam memahami konsep-konsep geometri yang lebih kompleks. Konsep ini tidak hanya terbatas pada perhitungan area segitiga itu sendiri, tetapi juga berfungsi sebagai dasar untuk memahami bangun ruang dan perhitungan volume.

• Volume Prisma: Untuk menghitung volume prisma (seperti prisma segitiga), kita menggunakan luas alas segitiga sebagai salah satu komponen utama. Rumus volume prisma adalah
  

  Volume = Luas Alas × Tinggi

  Di mana alasnya adalah segitiga. Dengan demikian, pemahaman tentang bagaimana menghitung luas segitiga menjadi kunci untuk menghitung volume prisma. Contohnya, jika kita memiliki prisma segitiga dengan luas alas segitiga 10 cm² dan tinggi prisma 5 cm, maka volume prisma adalah 50 cm³.

• Luas Permukaan Bangun Ruang: Konsep luas segitiga juga penting dalam menghitung luas permukaan bangun ruang yang memiliki sisi berbentuk segitiga, seperti limas. Untuk menghitung luas permukaan limas, kita perlu menghitung luas alas (yang bisa berbentuk segitiga) dan luas sisi-sisi tegak yang juga berbentuk segitiga. Jadi, pengetahuan tentang luas segitiga sangat penting dalam kasus ini.
• Perhitungan Jarak dalam Ruang Tiga Dimensi: Dalam geometri analitik, konsep luas segitiga digunakan dalam perhitungan jarak antara titik-titik dalam ruang tiga dimensi. Misalnya, untuk menemukan jarak antara dua titik, kita dapat menggunakan konsep segitiga siku-siku dan teorema Pythagoras, yang melibatkan perhitungan luas segitiga untuk menentukan panjang sisi-sisinya.

Dengan demikian, konsep luas segitiga tidak hanya berdiri sendiri, tetapi juga menjadi fondasi penting dalam memahami dan memecahkan masalah geometri yang lebih kompleks. Pemahaman yang kuat tentang luas segitiga membuka pintu ke pemahaman yang lebih mendalam tentang konsep-konsep geometri lainnya, yang sangat penting dalam berbagai bidang, mulai dari arsitektur hingga rekayasa.

Oke, mari kita mulai dengan dasar: menghitung luas segitiga. Rumusnya sederhana, tapi kadang kita butuh istirahat sejenak dari angka-angka. Nah, bagaimana kalau kita beralih ke sesuatu yang lebih santai? Pernahkah terpikir untuk membuat video selang waktu (time-lapse) yang keren? Dengan cara membuat selang waktu di hp Samsung , kamu bisa berkreasi dengan mudah.

Setelah pikiran segar, mari kembali ke soal segitiga, karena pemahaman konsepnya penting untuk soal-soal berikutnya!

Skenario Proyek: Merancang Taman Berbentuk Segitiga

Mari kita rancang sebuah proyek praktis yang melibatkan perhitungan luas segitiga. Proyek ini akan berfokus pada merancang taman berbentuk segitiga dengan mempertimbangkan luas lahan, biaya material, dan kebutuhan tanaman. Proyek ini akan membantu mengaplikasikan konsep luas segitiga dalam konteks dunia nyata.

Tujuan Proyek: Merancang taman berbentuk segitiga yang indah dan fungsional dengan anggaran yang efisien.

Langkah-langkah Proyek:

1. Penentuan Luas Lahan: Tentukan luas lahan yang tersedia untuk taman berbentuk segitiga. Misalnya, lahan yang tersedia berukuran 20 meter pada satu sisi dan tinggi 15 meter.
2. Perhitungan Luas Segitiga: Gunakan rumus luas segitiga (½ × alas × tinggi) untuk menghitung luas lahan yang tersedia. Dalam contoh ini, luasnya adalah ½ × 20 meter × 15 meter = 150 meter persegi.
3. Perencanaan Desain: Rencanakan desain taman, termasuk penempatan area tanaman, jalur setapak, dan elemen dekoratif. Pertimbangkan jenis tanaman yang akan ditanam dan kebutuhan ruang masing-masing tanaman.
4. Perhitungan Biaya Material: Hitung biaya material yang dibutuhkan, seperti tanah, pupuk, tanaman, batu paving untuk jalur setapak, dan elemen dekoratif lainnya. Perkirakan biaya per meter persegi untuk setiap material.
5. Perencanaan Penanaman: Hitung jumlah tanaman yang dibutuhkan berdasarkan luas area penanaman dan jarak tanam yang direkomendasikan untuk setiap jenis tanaman.
6. Evaluasi dan Optimasi: Evaluasi desain taman berdasarkan anggaran dan kebutuhan tanaman. Lakukan penyesuaian jika diperlukan untuk memastikan efisiensi biaya dan keindahan taman.

Hasil yang Diharapkan:

• Rancangan taman berbentuk segitiga yang lengkap dengan ukuran dan detail yang jelas.
• Perhitungan luas lahan, biaya material, dan jumlah tanaman yang dibutuhkan.
• Rencana anggaran yang terperinci.

Proyek ini tidak hanya mengaplikasikan konsep luas segitiga, tetapi juga mengajarkan keterampilan perencanaan, perhitungan biaya, dan pengambilan keputusan yang penting dalam konteks praktis.

Soal Latihan Luas Segitiga

Berikut adalah daftar soal latihan yang bervariasi tingkat kesulitannya, mulai dari soal sederhana hingga soal yang membutuhkan pemikiran kritis dan penerapan konsep secara kreatif. Setiap soal dilengkapi dengan kunci jawaban untuk memudahkan pembelajaran.

1. Soal Sederhana: Sebuah segitiga memiliki alas 10 cm dan tinggi 8 cm. Hitunglah luas segitiga tersebut.
• Kunci Jawaban: Luas = ½ × 10 cm × 8 cm = 40 cm²
2. Soal Sedang: Sebuah segitiga siku-siku memiliki sisi alas 6 cm dan sisi miring 10 cm. Hitunglah luas segitiga tersebut. (Petunjuk: Gunakan teorema Pythagoras untuk menemukan tinggi segitiga.)
• Kunci Jawaban: Tinggi = √(10²
  -6²) = 8 cm. Luas = ½ × 6 cm × 8 cm = 24 cm²
3. Soal Sulit: Sebuah taman berbentuk segitiga sama sisi dengan panjang sisi 12 meter. Hitunglah luas taman tersebut. (Petunjuk: Gunakan rumus luas segitiga sama sisi: Luas = (√3 / 4) × sisi²)
• Kunci Jawaban: Luas = (√3 / 4) × 12² = 62.35 m² (perkiraan)
4. Soal Kreatif: Sebuah logo perusahaan berbentuk segitiga dengan luas 50 cm². Jika alas segitiga adalah 10 cm, berapakah tinggi segitiga tersebut?
• Kunci Jawaban: Tinggi = (2 × Luas) / Alas = (2 × 50 cm²) / 10 cm = 10 cm
5. Soal Aplikasi: Sebuah lahan berbentuk segitiga akan ditanami rumput. Lahan tersebut memiliki alas 15 meter dan tinggi 10 meter. Jika biaya penanaman rumput per meter persegi adalah Rp 25.000, berapakah total biaya yang dibutuhkan?
• Kunci Jawaban: Luas = ½ × 15 meter × 10 meter = 75 m². Total Biaya = 75 m² × Rp 25.000/m² = Rp 1.875.000

Soal-soal ini dirancang untuk menguji pemahaman konsep luas segitiga dalam berbagai konteks, mulai dari perhitungan dasar hingga aplikasi praktis dan pemecahan masalah yang lebih kompleks.

Ilustrasi Deskriptif: Aplikasi Luas Segitiga

Konsep luas segitiga memiliki aplikasi yang luas dalam berbagai bidang, dari desain hingga analisis data. Mari kita lihat beberapa contoh bagaimana konsep ini digunakan dalam praktiknya.

1. Desain Logo: Banyak logo perusahaan dan merek terkenal menggunakan bentuk segitiga sebagai elemen desain utama. Segitiga memberikan kesan stabilitas, kekuatan, dan arah. Dalam desain logo, perhitungan luas segitiga sering digunakan untuk menentukan proporsi dan keseimbangan visual. Misalnya, desainer dapat menggunakan luas segitiga untuk memastikan bahwa elemen-elemen logo memiliki ukuran yang proporsional dan estetis.

Memahami cara menghitung luas segitiga itu krusial, kan? Rumusnya sederhana: 1/2 alas tinggi. Tapi, bagaimana jika kamu ingin memperdalam pengetahuanmu tentang matematika dan topik lainnya? Nah, Identif.id menyediakan berbagai sumber belajar yang bisa membantumu, mulai dari materi dasar hingga pembahasan yang lebih kompleks. Kembali ke segitiga, dengan memahami konsep dasar dan latihan soal, kamu akan mahir menghitung luasnya!

Contohnya adalah logo Adidas yang menggunakan tiga garis segitiga yang membentuk gunung, melambangkan tantangan dan tujuan.

2. Pembuatan Pola: Dalam bidang tekstil dan desain grafis, konsep luas segitiga digunakan untuk membuat pola yang kompleks dan menarik. Desainer dapat menggunakan berbagai ukuran dan bentuk segitiga untuk menciptakan pola repetitif atau unik. Perhitungan luas segitiga membantu dalam menentukan ukuran dan posisi elemen-elemen pola. Misalnya, pola sarang lebah sering kali menggunakan bentuk heksagonal yang terdiri dari segitiga sama sisi, yang perhitungan luasnya sangat penting untuk menentukan ukuran dan susunan pola.

3. Analisis Data: Dalam analisis data, konsep luas segitiga digunakan dalam berbagai metode visualisasi data, seperti diagram Voronoi dan triangulasi Delaunay. Diagram Voronoi membagi ruang menjadi area berdasarkan jarak terdekat ke titik-titik data, sementara triangulasi Delaunay menghubungkan titik-titik data untuk membentuk segitiga. Perhitungan luas segitiga digunakan untuk mengukur area yang dibentuk oleh data dan untuk menganalisis distribusi data. Misalnya, dalam analisis geospasial, luas segitiga digunakan untuk mengukur area yang dicakup oleh data dan untuk mengidentifikasi pola spasial.

4. Arsitektur dan Konstruksi: Konsep luas segitiga sangat penting dalam perencanaan dan konstruksi bangunan. Para arsitek dan insinyur menggunakan perhitungan luas segitiga untuk menghitung luas atap, dinding, dan elemen struktural lainnya. Pemahaman tentang luas segitiga membantu dalam menentukan jumlah material yang dibutuhkan, perencanaan tata letak, dan memastikan stabilitas struktur. Contohnya adalah perhitungan luas permukaan atap berbentuk segitiga pada rumah atau bangunan komersial.

Ilustrasi ini menunjukkan bahwa konsep luas segitiga memiliki aplikasi yang luas dan relevan dalam berbagai bidang, dari desain visual hingga analisis data dan konstruksi. Pemahaman yang kuat tentang konsep ini memungkinkan kita untuk memecahkan masalah praktis dan mengembangkan keterampilan berpikir spasial yang penting.

Penutupan

Jadi, telah dijelajahi dunia cara mengerjakan luas segitiga, mulai dari fondasi dasar hingga aplikasi yang lebih canggih. Telah dilihat bagaimana konsep sederhana ini menjadi landasan untuk memahami geometri yang lebih kompleks dan memecahkan masalah dunia nyata. Ingatlah, penguasaan rumus hanyalah awal. Kuncinya adalah kemampuan untuk mengidentifikasi, mengukur, dan menerapkan konsep ini secara kreatif dalam berbagai konteks.

Teruslah berlatih, bereksperimen, dan jangan takut untuk menjelajahi lebih jauh. Dunia geometri menunggu untuk dijelajahi, dan dengan pengetahuan tentang luas segitiga, akan memiliki alat yang dibutuhkan untuk menaklukkannya. Selamat bereksplorasi!

Kumpulan FAQ

Apa rumus dasar untuk menghitung luas segitiga?

Rumus dasar untuk menghitung luas segitiga adalah 1/2
– alas
– tinggi.

Bagaimana cara mengukur tinggi segitiga jika tidak ada garis yang tegak lurus ke alas?

Jika tidak ada garis yang tegak lurus, dapat menggunakan konsep trigonometri atau teorema Pythagoras, tergantung pada informasi yang tersedia (sudut atau panjang sisi).

Jenis segitiga apa saja yang ada?

Jenis segitiga meliputi segitiga siku-siku, sama kaki, sama sisi, dan sembarang.

Apakah satuan luas selalu dalam bentuk persegi?

Ya, satuan luas selalu dalam bentuk persegi, seperti cm², m², atau inci².