Cara Menghitung Bilangan Oktal Panduan Lengkap Konversi Dan Aritmatika

Cara menghitung bilangan oktal – Pernahkah Anda bertanya-tanya bagaimana komputer memahami angka? Di balik layar, sistem bilangan menjadi bahasa utama. Salah satunya adalah sistem bilangan oktal. Mari kita selami dunia oktal, sebuah sistem bilangan berbasis delapan yang memainkan peran penting dalam sejarah komputasi.

Artikel ini akan membawa Anda dalam perjalanan komprehensif untuk memahami cara menghitung bilangan oktal. Kita akan membahas definisi, konversi, aritmatika, dan penggunaan praktisnya, memastikan Anda memiliki pemahaman yang kuat tentang sistem bilangan yang menarik ini.

Table of Contents

Pengantar Bilangan Oktal

Sistem bilangan oktal, meskipun mungkin tidak sepopuler sistem desimal yang kita gunakan sehari-hari atau sistem biner yang menjadi jantung komputasi, memainkan peran penting dalam sejarah dan pemahaman dasar ilmu komputer. Artikel ini akan menggali lebih dalam tentang sistem bilangan oktal, mulai dari definisi dasar hingga aplikasinya, memberikan pemahaman komprehensif bagi pembaca yang ingin memperdalam pengetahuan mereka tentang representasi data dalam komputasi.

Mari kita mulai dengan memahami esensi dari sistem bilangan oktal.

Definisi dan Perbandingan

Sistem bilangan oktal adalah sistem bilangan berbasis 8, yang berarti menggunakan delapan digit berbeda untuk merepresentasikan angka: 0, 1, 2, 3, 4, 5, 6, dan 7. Setiap digit dalam angka oktal mewakili pangkat dari 8. Sistem ini menyediakan cara yang lebih ringkas untuk merepresentasikan angka biner, terutama dalam konteks memori komputer.

Mari kita bedah, menghitung bilangan oktal itu seperti bermain teka-teki angka, kan? Tapi, pernahkah terpikir, apa kaitannya dengan dunia digital yang kita jelajahi sehari-hari? Nah, terkadang, kita perlu mengakses informasi tanpa filter, seperti ketika mencari referensi. Jika Anda ingin membuka akses lebih luas di Yandex, ada caranya, yaitu dengan menonaktifkan pencarian aman. Setelah itu, kembali lagi ke oktal, angka-angka ini juga punya peran penting dalam representasi data di komputer, membuka wawasan baru tentang bagaimana informasi disimpan dan diproses.

Untuk lebih memahami perbedaan, mari kita bandingkan oktal dengan sistem bilangan desimal dan biner:

Fitur	Desimal (Basis 10)	Oktal (Basis 8)	Biner (Basis 2)
Digit yang Digunakan	0, 1, 2, 3, 4, 5, 6, 7, 8, 9	0, 1, 2, 3, 4, 5, 6, 7	0, 1
Basis	10	8	2
Nilai Tempat (Contoh)	…1000, 100, 10, 1, 0.1, 0.01…	…512, 64, 8, 1, 0.125, 0.015625…	…8, 4, 2, 1, 0.5, 0.25…
Contoh Representasi Angka	25 (dua puluh lima)	31 (tiga puluh satu)	11001 (dua puluh lima)
Kegunaan Umum	Sistem bilangan sehari-hari	Representasi data (sejarah), perizinan file di sistem Unix	Dasar komputasi, representasi data di memori komputer

Oktal lebih ringkas daripada biner karena setiap digit oktal dapat merepresentasikan tiga digit biner (karena 8 adalah 2 pangkat 3). Hal ini membuat representasi data lebih mudah dibaca dan dikelola, terutama dalam konteks memori komputer di mana representasi biner yang panjang bisa menjadi rumit.

Sejarah Singkat

Sistem bilangan oktal mulai digunakan secara luas dalam komputasi pada era komputer generasi awal dan pertengahan, khususnya pada komputer yang menggunakan memori berbasis core magnetik. Penggunaan oktal sangat membantu karena memberikan cara yang lebih mudah dan ringkas untuk merepresentasikan alamat memori dan data lainnya yang disimpan dalam format biner.

Beberapa komputer awal yang menggunakan oktal meliputi:

PDP-8 (Digital Equipment Corporation)
UNIVAC 1050
Beberapa model komputer IBM awal

Oktal menjadi populer sebelum munculnya sistem bilangan heksadesimal karena beberapa alasan. Pertama, konversi antara biner dan oktal relatif mudah, yang membuatnya ideal untuk pemrograman dan debugging pada saat itu. Kedua, oktal lebih ringkas daripada biner, yang mengurangi kebutuhan untuk menangani string biner yang panjang dan rentan kesalahan. Ketiga, arsitektur komputer awal seringkali memiliki ukuran word yang merupakan kelipatan dari tiga bit, sehingga oktal menjadi pilihan yang alami.

Transisi dari oktal ke heksadesimal terjadi seiring dengan perkembangan teknologi dan peningkatan ukuran word komputer. Heksadesimal, dengan basis 16, memungkinkan representasi yang lebih ringkas untuk ukuran word yang lebih besar (misalnya, 8, 16, atau 32 bit). Heksadesimal juga menjadi lebih populer karena kemudahan konversinya dengan biner dan kemampuannya untuk merepresentasikan lebih banyak informasi per digit.

Oke, mari kita mulai dengan bilangan oktal. Konsepnya mungkin terdengar rumit, tapi sebenarnya cukup sederhana jika kita pahami dasar-dasarnya. Nah, bicara soal yang rumit, pernahkah kamu merasa riwayat Instagram-mu terlalu berantakan? Untungnya, ada cara untuk membersihkannya. Kamu bisa simak langkah-langkahnya di cara menghapus riwayat instagram.

Kembali ke oktal, memahami konversi bilangan ini akan membuka wawasan baru dalam dunia digital. Jadi, jangan ragu untuk terus belajar!

Representasi dan Nilai Tempat

Angka oktal direpresentasikan menggunakan digit 0 hingga 7. Setiap digit dalam angka oktal memiliki nilai tempat yang berbeda, berdasarkan pangkat dari 8. Nilai tempat ini dimulai dari kanan dengan 8 ⁰ (1), kemudian 8 ¹ (8), 8 ² (64), dan seterusnya.

Berikut adalah tabel yang menunjukkan nilai tempat dalam sistem oktal:

Posisi Digit (dari kanan)	Nilai Tempat	Nilai Desimal
1	8⁰	1
2	8¹	8
3	8²	64
4	8³	512
…	…	…

Mari kita ambil contoh angka oktal
235. Untuk menghitung nilai desimalnya, kita kalikan setiap digit dengan nilai tempatnya dan menjumlahkannya:

Digit 5: 5
– 8 ⁰ = 5
– 1 = 5
Digit 3: 3
– 8 ¹ = 3
– 8 = 24
Digit 2: 2
– 8 ² = 2
– 64 = 128

Jadi, nilai desimal dari 235 ₈ adalah 5 + 24 + 128 = 157 ₁₀.

Konversi

Konversi antara sistem bilangan oktal dan sistem bilangan lainnya adalah keterampilan penting. Berikut adalah metode untuk melakukan konversi desimal ke oktal, oktal ke desimal, dan biner ke oktal (dan sebaliknya).

Desimal ke Oktal

Untuk mengkonversi angka desimal ke oktal, gunakan metode pembagian berulang dengan 8. Sisa dari setiap pembagian menjadi digit oktal, dibaca dari bawah ke atas.

Contoh 1: Konversi 25 ₁₀ ke oktal.

25 dibagi 8 = 3 sisa 1
3 dibagi 8 = 0 sisa 3

Membaca sisa dari bawah ke atas, kita mendapatkan 31. Jadi, 25 ₁₀ = 31 ₈.

Contoh 2: Konversi 100 ₁₀ ke oktal.

100 dibagi 8 = 12 sisa 4
12 dibagi 8 = 1 sisa 4
1 dibagi 8 = 0 sisa 1

Membaca sisa dari bawah ke atas, kita mendapatkan 144. Jadi, 100 ₁₀ = 144 ₈.

Contoh 3: Konversi 47.625 ₁₀ ke oktal.

Untuk bagian bulat:

47 dibagi 8 = 5 sisa 7
5 dibagi 8 = 0 sisa 5

Membaca sisa dari bawah ke atas, kita mendapatkan 57.

Untuk bagian pecahan, kalikan bagian pecahan dengan 8 secara berulang:

0.625
– 8 = 5.0

Membaca bagian bulat dari atas ke bawah, kita mendapatkan 5. Jadi, 0.625 ₁₀ = 0.5 ₈. Jadi, 47.625 ₁₀ = 57.5 ₈.

Oktal ke Desimal

Untuk mengkonversi angka oktal ke desimal, kalikan setiap digit dengan nilai tempatnya (pangkat dari 8) dan jumlahkan hasilnya.

Contoh 1: Konversi 31 ₈ ke desimal.

1
– 8 ⁰ = 1
– 1 = 1
3
– 8 ¹ = 3
– 8 = 24

Jadi, 31 ₈ = 1 + 24 = 25 ₁₀.

Contoh 2: Konversi 144 ₈ ke desimal.

4
– 8 ⁰ = 4
– 1 = 4
4
– 8 ¹ = 4
– 8 = 32
1
– 8 ² = 1
– 64 = 64

Jadi, 144 ₈ = 4 + 32 + 64 = 100 ₁₀.

Contoh 3: Konversi 57.5 ₈ ke desimal.

7
– 8 ⁰ = 7
– 1 = 7
5
– 8 ¹ = 5
– 8 = 40
5
– 8 ^-1 = 5
– 0.125 = 0.625

Jadi, 57.5 ₈ = 7 + 40 + 0.625 = 47.625 ₁₀.

Biner ke Oktal dan Sebaliknya

Konversi antara biner dan oktal sangat mudah karena basis 8 adalah pangkat dari 2. Untuk mengkonversi biner ke oktal, kelompokkan digit biner menjadi tiga-tiga, mulai dari kanan (untuk bilangan bulat) atau dari titik desimal (untuk bilangan pecahan). Kemudian, konversikan setiap kelompok tiga digit biner ke digit oktal yang setara.

Contoh: Konversi 110101 ₂ ke oktal.

Kelompokkan digit biner: 110 101
Konversikan setiap kelompok ke oktal: 110₂ = 6 ₈, 101 ₂ = 5 ₈

Jadi, 110101 ₂ = 65 ₈.

Untuk mengkonversi oktal ke biner, lakukan proses sebaliknya. Konversikan setiap digit oktal ke tiga digit biner yang setara.

Contoh: Konversi 37 ₈ ke biner.

Konversikan setiap digit oktal ke biner: 3₈ = 011 ₂, 7 ₈ = 111 ₂

Jadi, 37 ₈ = 011111 ₂ atau 11111 ₂ (nol di awal bisa diabaikan).

Blockquote

Sistem bilangan oktal adalah sistem bilangan berbasis 8 yang menggunakan digit 0-7. Setiap digit dalam angka oktal mewakili pangkat dari 8, mulai dari kanan (8⁰, 8 ¹, 8 ², dst.). Oktal berfungsi sebagai jembatan antara biner dan desimal, menyediakan representasi yang lebih ringkas daripada biner dan lebih mudah dikonversi.

Penggunaan Praktis

Meskipun penggunaan oktal telah berkurang seiring waktu, sistem ini masih memiliki beberapa aplikasi atau bidang yang pernah menggunakannya secara signifikan. Salah satunya adalah dalam sistem operasi berbasis Unix/Linux, di mana oktal digunakan untuk merepresentasikan izin akses file (read, write, execute) dalam format numerik. Misalnya, izin file 755 (oktal) berarti pemilik file memiliki akses baca, tulis, dan eksekusi, sementara grup dan pengguna lain hanya memiliki akses baca dan eksekusi.

Kelebihan utama penggunaan oktal adalah:

Kemudahan konversi antara biner dan oktal.
Representasi yang lebih ringkas dibandingkan biner, yang menghemat ruang dan mempermudah penanganan data.

Kekurangan penggunaan oktal adalah:

Tidak sepopuler heksadesimal dalam representasi data modern, sehingga pemahaman dan dukungan mungkin lebih terbatas.
Tidak efisien untuk ukuran word yang bukan kelipatan tiga bit.

Konversi Desimal ke Oktal

Konversi bilangan desimal ke oktal adalah proses mengubah representasi bilangan dari sistem bilangan berbasis 10 (desimal) ke sistem bilangan berbasis 8 (oktal). Proses ini penting dalam berbagai aplikasi ilmu komputer dan sistem digital. Konversi ini memungkinkan kita untuk merepresentasikan nilai desimal dalam format yang lebih ringkas atau sesuai dengan kebutuhan sistem tertentu. Artikel ini akan membahas secara rinci langkah-langkah, contoh, dan aplikasi dari konversi desimal ke oktal.

Langkah-Langkah Konversi Desimal ke Oktal

Konversi desimal ke oktal dilakukan menggunakan metode pembagian berulang dengan 8. Setiap langkah menghasilkan sisa pembagian yang akan menjadi digit oktal. Proses ini berlanjut hingga hasil bagi menjadi 0.

Pembagian Berulang: Bagi bilangan desimal dengan 8.
Catat Sisa: Simpan sisa pembagian. Sisa ini adalah digit oktal (0-7).
Ulangi: Bagi hasil bagi dari langkah sebelumnya dengan 8. Catat sisa.
Terus Berlanjut: Ulangi langkah 2 dan 3 hingga hasil bagi adalah 0.
Susun Sisa: Kumpulkan sisa pembagian, dimulai dari sisa terakhir hingga sisa pertama. Susunan ini membentuk bilangan oktal.

Konsep nilai tempat (place value) sangat penting dalam konversi ini. Dalam sistem oktal, setiap posisi digit mewakili pangkat dari 8. Digit paling kanan mewakili 8 ⁰ (1), digit berikutnya ke kiri mewakili 8 ¹ (8), lalu 8 ² (64), dan seterusnya. Dengan memahami nilai tempat, kita dapat mengonversi kembali bilangan oktal ke desimal untuk memverifikasi keakuratannya.

Contoh Soal Konversi Desimal ke Oktal

Berikut adalah lima contoh soal konversi bilangan desimal ke oktal, beserta perhitungan rinci dan verifikasi:

Contoh 1: Konversi 10 ke Oktal
- 10 ÷ 8 = 1 sisa 2
- 1 ÷ 8 = 0 sisa 1
- Hasil Oktal: 12 ₈
- Verifikasi: (1 x 8 ¹) + (2 x 8 ⁰) = 8 + 2 = 10
Contoh 2: Konversi 25 ke Oktal
- 25 ÷ 8 = 3 sisa 1
- 3 ÷ 8 = 0 sisa 3
- Hasil Oktal: 31 ₈
- Verifikasi: (3 x 8 ¹) + (1 x 8 ⁰) = 24 + 1 = 25
Contoh 3: Konversi 75 ke Oktal
- 75 ÷ 8 = 9 sisa 3
- 9 ÷ 8 = 1 sisa 1
- 1 ÷ 8 = 0 sisa 1
- Hasil Oktal: 113 ₈
- Verifikasi: (1 x 8 ²) + (1 x 8 ¹) + (3 x 8 ⁰) = 64 + 8 + 3 = 75
Contoh 4: Konversi 150 ke Oktal
- 150 ÷ 8 = 18 sisa 6
- 18 ÷ 8 = 2 sisa 2
- 2 ÷ 8 = 0 sisa 2
- Hasil Oktal: 226 ₈
- Verifikasi: (2 x 8 ²) + (2 x 8 ¹) + (6 x 8 ⁰) = 128 + 16 + 6 = 150
Contoh 5: Konversi 500 ke Oktal
- 500 ÷ 8 = 62 sisa 4
- 62 ÷ 8 = 7 sisa 6
- 7 ÷ 8 = 0 sisa 7
- Hasil Oktal: 764 ₈
- Verifikasi: (7 x 8 ²) + (6 x 8 ¹) + (4 x 8 ⁰) = 448 + 48 + 4 = 500

Demonstrasi Visual: Metode Pembagian Berulang

Metode pembagian berulang dapat divisualisasikan sebagai berikut: Bilangan desimal (misalnya, 27) dibagi dengan 8. Sisa pembagian dicatat. Hasil bagi kemudian dibagi lagi dengan 8, dan sisanya dicatat. Proses ini berlanjut hingga hasil bagi menjadi 0. Digit oktal dibentuk dengan membaca sisa pembagian dari bawah ke atas.

Misalnya, untuk mengonversi 27 ke oktal:

27 ÷ 8 = 3 sisa 3
3 ÷ 8 = 0 sisa 3

Sisa pembagian adalah 3 dan 3. Membaca dari bawah ke atas, bilangan oktal adalah 33 ₈.

Tabel Langkah Konversi Desimal ke Oktal

Kolom	Penjelasan	Contoh (Konversi 27 ke Oktal)
Langkah	Deskripsi singkat tentang apa yang harus dilakukan pada langkah tersebut.	Terapkan langkah tersebut pada contoh soal.
Pembagian	Bagi bilangan desimal dengan 8.	27 ÷ 8
Operasi	Pembagian.	Pembagian
Sisa	Sisa pembagian adalah nilai antara 0 dan 7, yang merupakan digit oktal.	3
Pembagian Lanjutan	Bagi hasil bagi dari langkah sebelumnya dengan 8.	3 ÷ 8
Operasi Lanjutan	Pembagian.	Pembagian
Sisa Lanjutan	Sisa pembagian adalah nilai antara 0 dan 7, yang merupakan digit oktal.	3
Hasil Oktal	Kumpulkan sisa pembagian dari bawah ke atas.	33₈ (3 dari sisa pertama, 3 dari sisa kedua)
Catatan	Pastikan untuk membagi hasil bagi hingga menjadi 0. Periksa kembali hasil konversi dengan mengonversi balik ke desimal.	Verifikasi: (3 x 8¹) + (3 x 8⁰) = 24 + 3 = 27

Blok Kode Konversi Desimal ke Oktal (Python)

“`pythondef decimal_to_octal(decimal_num): “”” Fungsi untuk mengkonversi bilangan desimal ke oktal. Args: decimal_num: Bilangan desimal yang akan dikonversi. Returns: String: Representasi oktal dari bilangan desimal. “”” if decimal_num == 0: return “0” # Kasus khusus untuk 0 octal_digits = [] while decimal_num > 0: remainder = decimal_num % 8 # Hitung sisa pembagian dengan 8 octal_digits.insert(0, str(remainder)) # Sisipkan sisa ke awal daftar decimal_num //= 8 # Lakukan pembagian integer return “”.join(octal_digits) # Gabungkan digit oktal menjadi string# Contoh penggunaandesimal = 25oktal = decimal_to_octal(desimal)print(f”Bilangan desimal desimal dalam oktal adalah: oktal”)“`

Relevansi dalam Ilmu Komputer dan Sistem Digital

Konversi desimal ke oktal sangat relevan dalam ilmu komputer dan sistem digital karena beberapa alasan:

Representasi Warna RGB: Dalam representasi warna RGB (Red, Green, Blue), setiap komponen warna (merah, hijau, biru) seringkali direpresentasikan dengan nilai 8-bit (0-255 desimal). Oktal dapat digunakan sebagai cara lain untuk merepresentasikan nilai-nilai ini, meskipun heksadesimal lebih umum digunakan.
Pengaturan Izin File Unix/Linux: Dalam sistem operasi berbasis Unix/Linux, izin file (read, write, execute) seringkali direpresentasikan menggunakan bilangan oktal. Setiap digit oktal mewakili izin untuk pemilik file, grup, dan pengguna lain. Contohnya, izin 755 berarti pemilik memiliki izin read, write, dan execute (7), grup memiliki read dan execute (5), dan pengguna lain memiliki read dan execute (5).
Pengalamatan Memori: Dalam beberapa arsitektur komputer, oktal digunakan untuk merepresentasikan alamat memori. Hal ini memudahkan pengelompokan bit dalam memori.
Debugging dan Analisis Sistem: Oktal juga digunakan dalam debugging dan analisis sistem untuk merepresentasikan nilai-nilai numerik dalam format yang lebih mudah dibaca oleh manusia.

Cara Menghitung Bilangan Oktal

Setelah memahami dasar-dasar bilangan oktal, mari kita selami proses konversi yang krusial: mengubah bilangan oktal menjadi representasi desimalnya. Konversi ini penting dalam berbagai bidang, mulai dari ilmu komputer hingga teknik digital, untuk memahami nilai sebenarnya dari bilangan oktal dalam sistem bilangan yang lebih familiar bagi kita.

Konversi Oktal ke Desimal

Konversi bilangan oktal ke desimal melibatkan pemahaman nilai tempat dan basis bilangan oktal. Setiap digit dalam bilangan oktal memiliki nilai tempat yang merupakan pangkat dari 8, dimulai dari 0 dari kanan ke kiri. Basis bilangan oktal adalah 8, yang berarti setiap posisi digit mewakili kelipatan dari 8.

Berikut adalah langkah-langkah konversi bilangan oktal ke desimal:

Identifikasi setiap digit dalam bilangan oktal.
Tentukan nilai tempat untuk setiap digit. Nilai tempat dimulai dari 8⁰ untuk digit paling kanan, 8 ¹ untuk digit berikutnya ke kiri, dan seterusnya.
Kalikan setiap digit dengan nilai tempatnya.
Jumlahkan semua hasil perkalian untuk mendapatkan nilai desimalnya.

Mari kita lihat beberapa contoh soal:

Contoh 1: Bilangan Oktal Dua Digit
Konversikan bilangan oktal 23 ₈ ke desimal.
1. Digit: 2 dan 3
2. Nilai Tempat: 2
  – 8 ¹ + 3
  – 8 ⁰
3. Perhitungan: (2
  – 8) + (3
  – 1) = 16 + 3 = 19
4. Hasil: 23 ₈ = 19 ₁₀
Contoh 2: Bilangan Oktal Tiga Digit
Konversikan bilangan oktal 145 ₈ ke desimal.
1. Digit: 1, 4, dan 5
2. Nilai Tempat: 1
  – 8 ² + 4
  – 8 ¹ + 5
  – 8 ⁰
3. Perhitungan: (1
  – 64) + (4
  – 8) + (5
  – 1) = 64 + 32 + 5 = 101
4. Hasil: 145 ₈ = 101 ₁₀
Contoh 3: Bilangan Oktal dengan Pecahan
Konversikan bilangan oktal 3.2 ₈ ke desimal.
1. Digit: 3 dan 2 (dengan titik desimal)
2. Nilai Tempat: 3
  – 8 ⁰ + 2
  – 8 ^-1
3. Perhitungan: (3
  – 1) + (2
  – 0.125) = 3 + 0.25 = 3.25
4. Hasil: 3.2 ₈ = 3.25 ₁₀

Metode perkalian dengan nilai tempat menggunakan rumus matematis berikut:

(d_n

8 ⁿ) + (d _n-1

8 ^n-1) + … + (d ₁

8 ¹) + (d ₀

8 ⁰) + (d _-1

8 ^-1) + …

di mana d _n adalah digit pada posisi n.

Berikut adalah diagram alir yang menggambarkan langkah-langkah konversi oktal ke desimal:

[Mulai]

[Input: Bilangan Oktal]

[Pisahkan digit dan tentukan nilai tempat (power of 8) untuk setiap digit]

[Kalikan setiap digit dengan nilai tempatnya]

[Jumlahkan semua hasil perkalian]

[Output: Nilai Desimal]

[Selesai]

Penanganan bilangan oktal dengan titik desimal (pecahan) melibatkan penggunaan pangkat negatif dari 8. Digit setelah titik desimal dikalikan dengan 8 ^-1, 8 ^-2, dan seterusnya. Contohnya, bilangan oktal 0.4 ₈ dikonversi menjadi (4
– 8 ^-1) = (4
– 0.125) = 0.5 ₁₀.

Tabel berikut merangkum nilai tempat (power of 8) untuk beberapa posisi digit:

Posisi Digit (dari kanan ke kiri)	Nilai Tempat (Power of 8)
0	8⁰ = 1
1	8¹ = 8
2	8² = 64
3	8³ = 512
4	8⁴ = 4096
-1 (setelah titik desimal)	8^-1 = 0.125
-2 (setelah titik desimal)	8^-2 = 0.015625

Mari kita konversikan bilangan oktal 73 ₈ ke desimal dan verifikasi menggunakan Python:

Perhitungan Manual: (7
- 8¹) + (3
- 8 ⁰) = (7
- 8) + (3
- 1) = 56 + 3 = 59 ₁₀
Kode Python:

def oktal_ke_desimal(oktal):
    desimal = int(oktal, 8)
    return desimal

oktal_number = "73"
desimal_result = oktal_ke_desimal(oktal_number)
print(f"Bilangan oktal oktal_number dalam desimal adalah: desimal_result")

Output:

Bilangan oktal 73 dalam desimal adalah: 59

Potensi kesalahan umum meliputi kesalahan dalam menentukan nilai tempat, kesalahan dalam perhitungan perkalian, dan kesalahan dalam menjumlahkan hasil perkalian. Untuk menghindarinya, pastikan untuk selalu memeriksa kembali setiap langkah konversi, gunakan kalkulator untuk memverifikasi perhitungan, dan berhati-hatilah dalam penempatan titik desimal.

Berikut adalah kuis singkat untuk menguji pemahaman Anda:

Konversikan 12₈ ke desimal.
Konversikan 345 ₈ ke desimal.
Konversikan 6.4 ₈ ke desimal.
Konversikan 27 ₈ ke desimal.
Konversikan 101 ₈ ke desimal.

Kunci Jawaban:

Konversi oktal ke desimal adalah proses penting dalam memahami nilai bilangan oktal dalam sistem desimal. Proses ini melibatkan pemahaman nilai tempat, perkalian digit dengan nilai tempatnya, dan penjumlahan hasil perkalian. Pemahaman yang baik tentang langkah-langkah ini, serta kemampuan untuk menghindari kesalahan umum, sangat penting untuk keberhasilan konversi.

Konversi Biner ke Oktal

Konversi biner ke oktal adalah proses krusial dalam dunia komputasi, khususnya dalam representasi data dan manipulasi bit. Proses ini memungkinkan kita untuk menyederhanakan representasi bilangan biner yang panjang menjadi format yang lebih ringkas, memudahkan pembacaan dan pemahaman. Mari kita telusuri lebih dalam tentang bagaimana konversi ini dilakukan.

Metode Konversi Biner ke Oktal

Konversi biner ke oktal didasarkan pada prinsip pengelompokan bit biner menjadi grup-grup yang terdiri dari tiga bit. Setiap grup tiga bit ini kemudian dikonversi menjadi satu digit oktal. Dasar teori di balik ini adalah bahwa sistem oktal (basis 8) menggunakan delapan simbol (0-7) untuk merepresentasikan nilai. Setiap digit oktal dapat direpresentasikan dengan tiga bit biner (2 ³ = 8). Proses ini efisien karena memungkinkan kita untuk dengan mudah mengubah representasi biner yang panjang menjadi format yang lebih mudah dikelola.

Contoh Konversi Biner ke Oktal

Mari kita lihat beberapa contoh konversi biner ke oktal:

Contoh 1: Konversi 101101

Langkah-langkah:
- Kelompokkan bit biner menjadi grup tiga bit dari kanan: 101 101
- Konversikan setiap grup tiga bit ke digit oktal:
- Gabungkan digit oktal: 55 ₈
Jadi, 101101 ₂ = 55 ₈
Contoh 2: Konversi 11001110

Langkah-langkah:
- Kelompokkan bit biner menjadi grup tiga bit dari kanan: 011 001 110 (tambahkan 0 di depan jika diperlukan untuk melengkapi grup)
- Konversikan setiap grup tiga bit ke digit oktal:
- Gabungkan digit oktal: 316 ₈
Jadi, 11001110 ₂ = 316 ₈
Contoh 3: Konversi 10101

Langkah-langkah:
- Kelompokkan bit biner menjadi grup tiga bit dari kanan: 010 101 (tambahkan 0 di depan jika diperlukan untuk melengkapi grup)
- Konversikan setiap grup tiga bit ke digit oktal:
- Gabungkan digit oktal: 25 ₈
Jadi, 10101 ₂ = 25 ₈

Pengelompokan Digit Biner dalam Konversi Biner ke Oktal

Proses konversi biner ke oktal secara visual melibatkan pengelompokan bit biner. Pengelompokan ini dilakukan dari kanan ke kiri, dimulai dengan tiga bit pertama. Jika jumlah bit tidak habis dibagi tiga, bit yang tersisa di sebelah kiri akan ditambahkan nol di depannya untuk membentuk grup tiga bit yang lengkap. Setiap grup tiga bit kemudian diwakili oleh satu digit oktal.

Ilustrasi visualnya bisa berupa diagram yang menunjukkan pengelompokan bit biner, dengan setiap grup tiga bit ditandai dan dikonversi ke digit oktal yang sesuai. Misalnya, untuk biner 11010110, diagram akan menunjukkan:

110 (grup pertama) -> 6
101 (grup kedua) -> 5
110 (grup ketiga) -> 6

Sehingga hasilnya adalah 326 ₈

Mari kita bedah cara menghitung bilangan oktal, sistem berbasis delapan yang seringkali terasa rumit bagi sebagian orang. Tapi, pernahkah terpikir bagaimana detail rumit ini bisa disederhanakan, layaknya memahami proporsi dan detail saat kita belajar cara menggambar gaun pengantin ? Sama seperti kita perlu memahami struktur dasar gaun sebelum menambahkan detail, begitu pula dengan oktal. Kembali ke oktal, setelah memahami dasar, perhitungan akan terasa lebih mudah dan menyenangkan.

Pengelompokan ini sangat berkaitan dengan basis 8 karena setiap grup tiga bit biner memiliki 2 ³ = 8 kemungkinan kombinasi, yang sesuai dengan delapan digit dalam sistem oktal (0-7).

Tabel Perbandingan Nilai Biner, Oktal, Desimal, dan Heksadesimal

Berikut adalah tabel yang membandingkan nilai biner, oktal, desimal, dan heksadesimal untuk 16 angka pertama:

Biner	Oktal	Desimal	Heksadesimal
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

Implementasi Konversi Biner ke Oktal dalam Python

Konversi biner ke oktal dapat diimplementasikan dengan mudah dalam bahasa pemrograman Python. Berikut adalah contoh kode sederhana:

def biner_ke_oktal(biner):
    """
    Fungsi untuk mengkonversi bilangan biner ke oktal.
    """
    # Pastikan input adalah string
    biner = str(biner)
    # Tambahkan '0' di depan jika panjang biner bukan kelipatan 3
    while len(biner) % 3 != 0:
        biner = '0' + biner

    oktal = ''
    # Konversi setiap grup 3 bit ke oktal
    for i in range(0, len(biner), 3):
        grup_biner = biner[i:i+3]
        desimal = int(grup_biner, 2) # Konversi biner ke desimal
        oktal += str(desimal)

    return oktal

# Contoh penggunaan
biner = "101101"
oktal = biner_ke_oktal(biner)
print(f"Bilangan biner biner dalam oktal adalah: oktal") # Output: 55

Penjelasan kode:

Fungsi biner_ke_oktal(biner) menerima string biner sebagai input.
Kode memastikan bahwa input adalah string.
Kode menambahkan ‘0’ di depan jika panjang biner bukan kelipatan 3.
Kode melakukan iterasi melalui string biner, mengambil grup tiga bit.
Setiap grup tiga bit dikonversi ke desimal menggunakan int(grup_biner, 2).
Nilai desimal kemudian dikonversi ke string dan ditambahkan ke string oktal.
Fungsi mengembalikan string oktal.

Perbandingan Konversi Biner ke Oktal dan Heksadesimal

Perbedaan utama antara konversi biner ke oktal dan biner ke heksadesimal terletak pada pengelompokan bit dan basis yang digunakan. Dalam konversi biner ke oktal, bit dikelompokkan menjadi grup tiga bit (2 ³ = 8), sedangkan dalam konversi biner ke heksadesimal, bit dikelompokkan menjadi grup empat bit (2 ⁴ = 16). Sistem oktal menggunakan basis 8 (digit 0-7), sedangkan sistem heksadesimal menggunakan basis 16 (digit 0-9 dan A-F).

Keuntungan Menggunakan Sistem Oktal

Sistem oktal menawarkan cara yang lebih ringkas untuk merepresentasikan bilangan biner dibandingkan dengan representasi biner itu sendiri. Hal ini mempermudah pembacaan dan penulisan nilai biner, terutama dalam konteks pemrograman tingkat rendah dan manipulasi bit.

Potensi Penggunaan Konversi Biner ke Oktal

Konversi biner ke oktal memiliki potensi penggunaan dalam berbagai konteks, termasuk:

Penyimpanan Data: Dalam sistem penyimpanan data, oktal dapat digunakan untuk merepresentasikan data biner dalam format yang lebih ringkas, mengurangi kebutuhan penyimpanan.
Representasi Data: Dalam beberapa sistem, oktal digunakan untuk merepresentasikan izin akses file (misalnya, pada sistem operasi Unix-like), di mana setiap digit oktal mewakili izin untuk pemilik, grup, dan pengguna lain.

Soal Latihan Konversi Biner ke Oktal

Konversikan 1101101₂ ke oktal.
Konversikan 101110010 ₂ ke oktal.
Konversikan 111000111 ₂ ke oktal.

Kunci Jawaban:

655₈
672 ₈
707 ₈

Penanganan Bilangan Biner Negatif dalam Konversi ke Oktal

Penanganan bilangan biner negatif dalam konversi ke oktal biasanya melibatkan penggunaan komplemen dua. Komplemen dua adalah representasi bilangan negatif dalam sistem biner. Untuk mengkonversi bilangan negatif ke oktal, pertama-tama kita perlu menghitung komplemen dua dari bilangan biner tersebut. Kemudian, kita dapat mengkonversi hasil komplemen dua ke oktal menggunakan metode yang sama seperti konversi bilangan biner positif. Sebagai contoh, jika kita memiliki bilangan biner negatif -5 (dalam representasi komplemen dua, misalnya, 11111011), kita akan mengkonversi 11111011 ke oktal (373 ₈).

Penting untuk dicatat bahwa hasil oktal ini mewakili nilai negatif dalam konteks komplemen dua.

Konversi Oktal ke Biner

Proses konversi bilangan oktal ke biner merupakan kebalikan dari konversi biner ke oktal. Bilangan oktal, yang berbasis 8, dapat dikonversi menjadi bilangan biner, yang berbasis 2, dengan cara yang relatif mudah. Setiap digit dalam bilangan oktal diwakili oleh tiga digit biner. Metode ini sangat berguna dalam ilmu komputer dan rekayasa digital, di mana konversi antar sistem bilangan sering diperlukan.

Cara Mengkonversi Bilangan Oktal ke Biner

Konversi oktal ke biner melibatkan pengubahan setiap digit oktal menjadi representasi biner tiga digit yang setara. Proses ini dilakukan secara terpisah untuk setiap digit dalam bilangan oktal, dan hasilnya kemudian digabungkan untuk membentuk bilangan biner yang lengkap.

Identifikasi Setiap Digit Oktal: Pisahkan bilangan oktal menjadi digit-digit individual.
Konversi Setiap Digit ke Biner: Ubah setiap digit oktal menjadi ekuivalen biner tiga digitnya. Gunakan tabel konversi sebagai referensi (lihat tabel di bawah).
Gabungkan Digit Biner: Gabungkan semua digit biner yang telah dikonversi untuk mendapatkan representasi biner akhir dari bilangan oktal.

Contoh Konversi Bilangan Oktal (35) ke Biner

Mari kita konversikan bilangan oktal 35 ke biner. Ikuti langkah-langkah berikut:

Pisahkan Digit: Bilangan oktal 35 terdiri dari dua digit: 3 dan 5.
Konversi Digit:
- Digit 3 dalam oktal setara dengan 011 dalam biner.
- Digit 5 dalam oktal setara dengan 101 dalam biner.
Gabungkan: Gabungkan digit biner yang telah dikonversi: 011101. Jadi, bilangan oktal 35 sama dengan 011101 dalam biner.

Demonstrasi Konversi Setiap Digit Oktal Menjadi Tiga Digit Biner

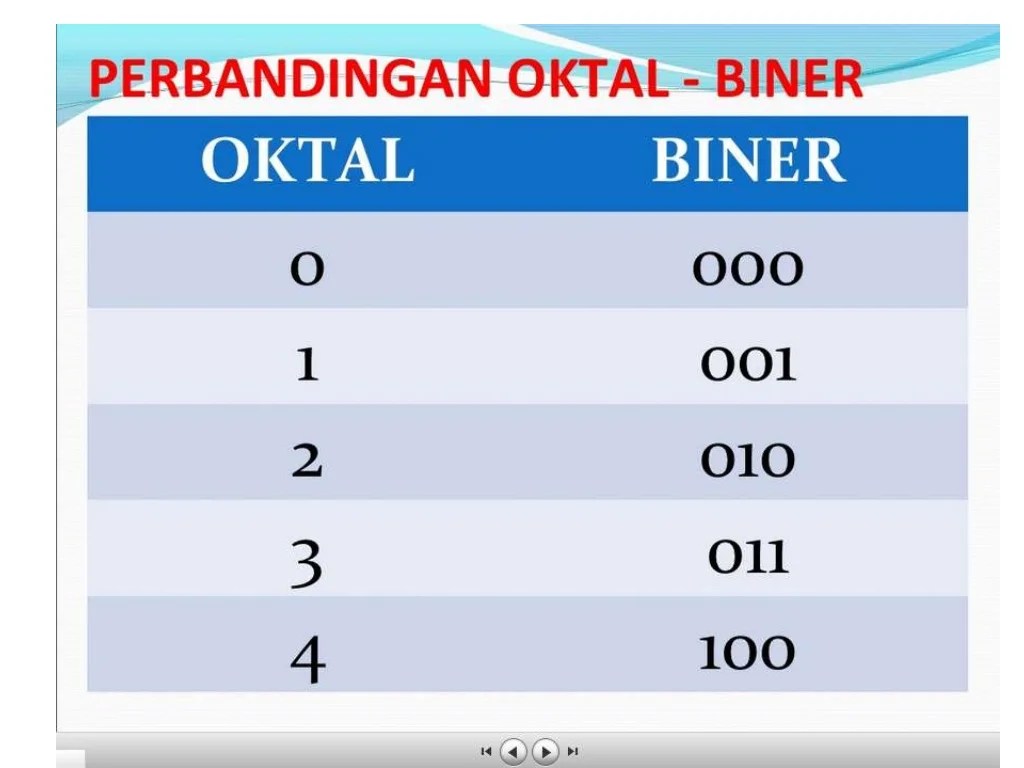
Konversi setiap digit oktal menjadi tiga digit biner mengikuti aturan yang konsisten. Setiap digit oktal memiliki representasi biner unik yang terdiri dari tiga bit. Tabel berikut menunjukkan konversi untuk setiap digit oktal:

Digit Oktal	Representasi Biner
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Infografis Konversi Oktal ke Biner

Infografis berikut memberikan gambaran visual tentang konversi oktal ke biner. Infografis ini menampilkan setiap digit oktal dan padanan binernya, yang disajikan dalam format yang mudah dipahami. Ini sangat berguna untuk memahami konsep konversi secara cepat dan efisien.

Deskripsi Infografis: Infografis ini menampilkan kolom vertikal yang terbagi menjadi dua bagian. Bagian kiri berisi digit oktal dari 0 hingga 7, masing-masing dalam kotak terpisah. Di sebelah kanan setiap digit oktal, terdapat kotak yang berisi representasi biner tiga digitnya. Misalnya, di samping digit oktal 3, terdapat kotak yang menampilkan 011. Infografis ini menggunakan warna yang konsisten untuk menyoroti setiap pasangan oktal dan biner, membuat proses konversi mudah diikuti.

Aritmatika Bilangan Oktal

Setelah memahami dasar-dasar bilangan oktal, mari kita selami lebih dalam ke operasi aritmatika. Penjumlahan adalah operasi dasar yang sangat penting dalam sistem bilangan oktal. Kemampuan untuk menjumlahkan bilangan oktal adalah fondasi untuk memahami operasi aritmatika lainnya, seperti pengurangan, perkalian, dan pembagian. Mari kita bahas cara melakukan penjumlahan pada bilangan oktal.

Penjumlahan Bilangan Oktal

Penjumlahan bilangan oktal dilakukan dengan cara yang mirip dengan penjumlahan desimal, tetapi dengan perbedaan mendasar pada basisnya. Karena basis oktal adalah 8, kita harus memperhatikan carry-over (sisa) jika hasil penjumlahan dua digit melebihi 7. Prosesnya melibatkan penjumlahan digit-digit pada posisi yang sama, dimulai dari digit paling kanan (satuan), kemudian memproses digit berikutnya (delapanan, enam puluh empatan, dan seterusnya).

Mari kita lihat contoh soal penjumlahan bilangan oktal: 12 + 23.

Langkah 1: Jumlahkan digit paling kanan (satuan): 2 + 3 = 5. Karena 5 kurang dari 8, kita tuliskan 5 pada posisi satuan.
Langkah 2: Jumlahkan digit berikutnya (delapanan): 1 + 2 = 3. Kita tuliskan 3 pada posisi delapanan.

Jadi, 12 ₈ + 23 ₈ = 35 ₈.

Penanganan Carry-Over (Sisa) dalam Penjumlahan Oktal

Ketika hasil penjumlahan dua digit oktal melebihi 7, kita harus melakukan carry-over. Ini berarti kita membagi hasil penjumlahan dengan 8. Sisa dari pembagian menjadi digit pada posisi tersebut, dan hasil bagi (quotient) menjadi carry-over ke posisi berikutnya (kiri).

Sebagai contoh, mari kita jumlahkan 65 ₈ + 27 ₈:

Langkah 1: Jumlahkan digit paling kanan (satuan): 5 + 7 = 12. Karena 12 lebih besar dari 7, kita bagi 12 dengan 8. Hasilnya adalah 1 dengan sisa 4. Kita tuliskan 4 pada posisi satuan dan carry-over 1 ke posisi berikutnya.
Langkah 2: Jumlahkan digit berikutnya (delapanan), termasuk carry-over: 6 + 2 + 1 (carry-over) = 9. Karena 9 lebih besar dari 7, kita bagi 9 dengan 8. Hasilnya adalah 1 dengan sisa 1. Kita tuliskan 1 pada posisi delapanan dan carry-over 1 ke posisi berikutnya (ratusan).
Langkah 3: Karena tidak ada digit lain untuk dijumlahkan, kita tuliskan carry-over 1 pada posisi ratusan.

Jadi, 65 ₈ + 27 ₈ = 114 ₈.

Aturan Penjumlahan Bilangan Oktal:

Jumlahkan digit-digit pada posisi yang sama.

Jika hasil penjumlahan kurang dari 8, tuliskan hasilnya pada posisi tersebut.

Jika hasil penjumlahan sama dengan atau lebih besar dari 8, bagi hasil penjumlahan dengan 8. Tuliskan sisa pembagian pada posisi tersebut dan carry-over hasil bagi ke posisi berikutnya (kiri).

Ulangi langkah-langkah di atas untuk setiap posisi digit.

Aritmatika Bilangan Oktal

Setelah memahami dasar-dasar konversi dan representasi bilangan oktal, kita akan beralih ke operasi aritmatika dasar. Aritmatika bilangan oktal memungkinkan kita melakukan perhitungan langsung dengan bilangan oktal, mirip dengan cara kita melakukan perhitungan dengan bilangan desimal. Pemahaman yang baik tentang aritmatika oktal sangat penting untuk aplikasi yang melibatkan sistem bilangan oktal, terutama dalam bidang komputer dan sistem digital.

Pengurangan dalam Bilangan Oktal

Pengurangan dalam sistem bilangan oktal mengikuti prinsip yang serupa dengan pengurangan dalam sistem desimal, namun dengan basis 8. Ini berarti kita hanya menggunakan digit 0 hingga 7. Prosesnya melibatkan pengurangan digit demi digit, dimulai dari digit paling kanan (least significant digit/LSD). Jika digit pengurang lebih besar daripada digit yang dikurangi, kita perlu “meminjam” (borrow) dari digit di sebelah kirinya.

Mari kita lihat contoh sederhana.

Contoh Soal Pengurangan Bilangan Oktal: 34₈
-12 ₈

Untuk menghitungnya, kita susun soalnya secara vertikal:

34 ₈

Baiklah, mari kita mulai dengan bilangan oktal. Konversi bilangan oktal memang sedikit teknis, melibatkan pemahaman sistem basis 8. Tapi, tahukah Anda, ketelitian yang sama diperlukan saat ingin menyaksikan pertandingan Thomas Cup? Ya, untuk memastikan tidak ketinggalan aksi para pebulu tangkis hebat, Anda perlu tahu cara live streaming thomas cup dengan tepat. Kembali ke oktal, setelah memahami dasarnya, konversi menjadi lebih mudah, sama seperti menikmati pertandingan olahraga favorit Anda.

-12 ₈
——

Pertama, kurangkan digit paling kanan (satuan): 4 – 2 = 2.

34 ₈

-12 ₈
——
2

Kemudian, kurangkan digit di sebelah kiri (delapanan): 3 – 1 = 2.

34 ₈

-12 ₈
——
22 ₈

Jadi, 34 ₈
-12 ₈ = 22 ₈.

Meminjam (Borrow) dalam Pengurangan Oktal

Konsep “meminjam” dalam pengurangan oktal sedikit berbeda dari pengurangan desimal karena basisnya yang berbeda. Ketika kita perlu meminjam, kita meminjam 1 dari digit di sebelah kiri, yang setara dengan menambahkan 8 ke digit yang sedang dikurangi (karena basisnya adalah 8).

Sebagai contoh, mari kita lihat pengurangan 42 ₈
-15 ₈.

42 ₈

-15 ₈
——

Pertama, kita mencoba mengurangkan digit satuan: 2 – 5. Karena 2 lebih kecil dari 5, kita perlu meminjam dari digit di sebelah kiri (4).

Kita meminjam 1 dari 4, yang mengubah 4 menjadi 3. Kemudian, kita menambahkan 8 ke 2 (karena basisnya adalah 8), yang menghasilkan 10 (dalam desimal). Sekarang kita memiliki 10 – 5 = 5.

3(10) ₈

-1 5 ₈
——
5

Selanjutnya, kurangkan digit delapanan: 3 – 1 = 2.

3(10) ₈

-1 5 ₈
——
25 ₈

Jadi, 42 ₈
-15 ₈ = 25 ₈.

Perbandingan Penjumlahan dan Pengurangan Oktal

Berikut adalah tabel yang membandingkan operasi penjumlahan dan pengurangan dalam sistem bilangan oktal:

Operasi	Contoh	Hasil
Penjumlahan	53₈ + 24₈	77₈
Pengurangan (tanpa meminjam)	35₈ – 12₈	23₈
Pengurangan (dengan meminjam)	61₈ – 25₈	34₈

Aritmatika Bilangan Oktal: Perkalian

Setelah memahami dasar-dasar penjumlahan dan pengurangan bilangan oktal, langkah selanjutnya adalah mempelajari perkalian. Perkalian dalam sistem bilangan oktal mengikuti prinsip yang sama dengan perkalian desimal, tetapi dengan penyesuaian pada basis 8. Mari kita selami lebih dalam tentang cara melakukan perkalian oktal.

Perkalian bilangan oktal melibatkan penggunaan tabel perkalian oktal dan penanganan carry-over, mirip dengan yang kita lakukan dalam perkalian desimal. Namun, karena kita bekerja dalam basis 8, kita perlu memperhatikan bahwa setiap kali hasil perkalian melebihi 7, kita harus melakukan konversi dan membawa nilai ke kolom berikutnya.

Langkah-Langkah Perkalian Bilangan Oktal

Proses perkalian bilangan oktal melibatkan beberapa langkah penting:

Persiapan: Susun bilangan oktal yang akan dikalikan seperti halnya perkalian desimal.
Perkalian Digit: Kalikan setiap digit dari bilangan pengali dengan setiap digit dari bilangan yang dikalikan.
Konversi: Jika hasil perkalian dua digit lebih besar dari 7, konversikan hasil tersebut ke dalam representasi oktal yang benar (digit satuan dan carry-over).
Penempatan: Tempatkan hasil perkalian dan carry-over di kolom yang sesuai.
Penjumlahan: Jumlahkan semua hasil perkalian kolom demi kolom, termasuk carry-over.

Contoh Soal Perkalian Bilangan Oktal

Mari kita lihat beberapa contoh untuk memahami proses perkalian oktal:

Contoh 1: Perkalian Sederhana (23₈ x 4₈)

Langkah-langkah:

Kalikan 4 dengan 3 (digit paling kanan dari 23₈): 4 x 3 = 12.
Konversi 12 ke oktal. Dalam oktal, 12 sama dengan 14₈ (1 x 8¹ + 4 x 8⁰). Tulis 4 dan bawa 1.
Kalikan 4 dengan 2 (digit berikutnya dari 23₈): 4 x 2 = 8.
Tambahkan carry-over 1: 8 + 1 = 9.
Konversi 9 ke oktal. Dalam oktal, 9 sama dengan 11₈ (1 x 8¹ + 1 x 8⁰). Tulis 11.

Ilustrasi:

  2 3₈
x 4₈
-----
  1 1 4₈

Jadi, 23₈ x 4₈ = 114₈.

Contoh 2: Perkalian dengan Carry-Over (35₈ x 6₈)

Langkah-langkah:

Kalikan 6 dengan 5: 6 x 5 = 30.
Konversi 30 ke oktal. Dalam oktal, 30 sama dengan 36₈ (3 x 8¹ + 6 x 8⁰). Tulis 6 dan bawa 3.
Kalikan 6 dengan 3: 6 x 3 = 18.
Tambahkan carry-over 3: 18 + 3 = 21.
Konversi 21 ke oktal. Dalam oktal, 21 sama dengan 25₈ (2 x 8¹ + 5 x 8⁰). Tulis 25.

Ilustrasi:

  3 5₈
x 6₈
-----
  2 5 6₈

Jadi, 35₈ x 6₈ = 256₈.

Contoh 3: Perkalian dengan Dua Bilangan Oktal (12₈ x 34₈)

Langkah-langkah:

Kalikan 4 dengan 2: 4 x 2 = 8. Konversi 8 ke oktal (10₈). Tulis 0 dan bawa 1.
Kalikan 4 dengan 1: 4 x 1 =
4. Tambahkan carry-over 1

4 + 1 = 5. Tulis 5.
Kalikan 3 dengan 2: 3 x 2 = 6. Tulis 6 (geser satu posisi ke kiri).
Kalikan 3 dengan 1: 3 x 1 = 3. Tulis 3 (geser satu posisi ke kiri).
Jumlahkan hasil perkalian: 50₈ + 36₈ = 620₈

Ilustrasi:

  1 2₈
x 3 4₈
-------
    5 0₈
  3 6₈
-------
  6 2 0₈

Jadi, 12₈ x 34₈ = 620₈.

Penanganan Hasil Perkalian Lebih Besar dari 7

Ketika hasil perkalian dua digit lebih besar dari 7, kita perlu melakukan konversi ke representasi oktal. Berikut adalah tabel konversi untuk membantu:

Desimal	Oktal	Penjelasan
8	10₈	1 x 8¹ + 0 x 8⁰
9	11₈	1 x 8¹ + 1 x 8⁰
10	12₈	1 x 8¹ + 2 x 8⁰
11	13₈	1 x 8¹ + 3 x 8⁰
12	14₈	1 x 8¹ + 4 x 8⁰
13	15₈	1 x 8¹ + 5 x 8⁰
14	16₈	1 x 8¹ + 6 x 8⁰
15	17₈	1 x 8¹ + 7 x 8⁰
16	20₈	2 x 8¹ + 0 x 8⁰

Implementasi Perkalian Oktal dalam Python

Berikut adalah contoh kode Python untuk melakukan perkalian bilangan oktal:

def oktal_to_desimal(oktal):
    desimal = 0
    for i, digit in enumerate(reversed(str(oktal))):
        desimal += int(digit)
- (8
-* i)
    return desimal

def desimal_to_oktal(desimal):
    if desimal == 0:
        return 0
    oktal = ""
    while desimal > 0:
        sisa = desimal % 8
        oktal = str(sisa) + oktal
        desimal //= 8
    return int(oktal)

def perkalian_oktal(oktal1, oktal2):
    desimal1 = oktal_to_desimal(oktal1)
    desimal2 = oktal_to_desimal(oktal2)
    hasil_desimal = desimal1
- desimal2
    hasil_oktal = desimal_to_oktal(hasil_desimal)
    return hasil_oktal

# Contoh penggunaan
angka1 = 23
angka2 = 4
hasil = perkalian_oktal(angka1, angka2)
print(f"angka1₈ x angka2₈ = hasil₈") # Output: 23₈ x 4₈ = 114₈

angka1 = 35
angka2 = 6
hasil = perkalian_oktal(angka1, angka2)
print(f"angka1₈ x angka2₈ = hasil₈") # Output: 35₈ x 6₈ = 256₈

angka1 = 12
angka2 = 34
hasil = perkalian_oktal(angka1, angka2)
print(f"angka1₈ x angka2₈ = hasil₈") # Output: 12₈ x 34₈ = 620₈

Tabel Perkalian Oktal

Tabel berikut merangkum hasil perkalian untuk digit oktal dari 0 hingga 7:

x	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7
2	2	4	6	10	12	14	16
3	3	6	11	14	17	22	25
4	4	10	14	20	24	30	34
5	5	12	17	24	31	36	43
6	6	14	22	30	36	44	52
7	7	16	25	34	43	52	61

Memahami aritmatika oktal, khususnya perkalian, sangat penting dalam bidang ilmu komputer dan rekayasa digital. Sistem oktal digunakan dalam beberapa konteks untuk merepresentasikan nilai biner secara ringkas, dan kemampuan untuk melakukan perhitungan dalam basis 8 adalah keterampilan dasar bagi siapa saja yang bekerja dengan sistem digital.

Aritmatika Bilangan Oktal: Pembagian

Pembagian dalam sistem bilangan oktal mungkin terdengar asing bagi sebagian orang, tetapi prinsip dasarnya serupa dengan pembagian dalam sistem desimal yang lebih familiar. Artikel ini akan membahas secara mendalam tentang bagaimana pembagian oktal dilakukan, memberikan contoh-contoh praktis, dan menjelaskan bagaimana menangani sisa dalam perhitungan tersebut. Tujuannya adalah untuk memberikan pemahaman yang komprehensif dan praktis tentang aritmatika pembagian dalam sistem bilangan oktal.

Mari kita selami lebih dalam!

Penjelasan Mendalam tentang Pembagian Oktal

Pembagian oktal adalah proses membagi suatu bilangan oktal (bilangan berbasis 8) dengan bilangan oktal lainnya. Sama seperti pembagian desimal, tujuannya adalah untuk menentukan berapa kali pembagi (divisor) “masuk” ke dalam bilangan yang dibagi (dividend). Perbedaan utama terletak pada basis bilangan: dalam oktal, kita menggunakan basis 8, yang berarti hanya ada delapan digit yang valid (0-7). Setiap posisi digit dalam bilangan oktal mewakili pangkat dari 8, dimulai dari kanan dengan 8^0, kemudian 8^1, 8^2, dan seterusnya.

Proses pembagian oktal mengikuti langkah-langkah yang mirip dengan pembagian desimal. Kita mulai dengan membagi digit paling kiri dari bilangan yang dibagi dengan pembagi. Jika pembagi lebih besar dari digit pertama, kita mempertimbangkan dua digit pertama, dan seterusnya. Kita mencari berapa kali pembagi “masuk” ke dalam bagian dari bilangan yang dibagi. Hasilnya (kuosien) ditulis di atas, dan kemudian dikalikan dengan pembagi.

Hasil perkalian ini dikurangkan dari bagian bilangan yang dibagi yang sedang kita kerjakan. Proses ini diulang sampai semua digit bilangan yang dibagi telah diperhitungkan.

Konsep “borrowing” (peminjaman) dalam pembagian oktal juga perlu dipahami. Jika dalam pengurangan kita perlu “meminjam” dari digit di sebelah kiri, kita meminjam “8” (bukan 10 seperti dalam desimal) karena kita bekerja dalam basis 8. Misalnya, jika kita perlu mengurangkan 5 dari 2 dalam oktal, kita “meminjam” 8 dari digit di sebelah kiri, sehingga 2 menjadi 10 (dalam desimal) + 2 = 10 (dalam oktal).

Jadi, 10 – 5 = 5 dalam oktal.

Contoh Soal Pembagian Oktal yang Beragam

Mari kita lihat beberapa contoh untuk memperjelas proses pembagian oktal:

Contoh 1: Pembagian sederhana tanpa sisa (24_8 / 3_8)

“““ 24_8 / 3_8 = ? Langkah 1: Bagi 2 (digit pertama dari 24_8) dengan 3. Karena 3 lebih besar dari 2, kita pertimbangkan

24. Langkah 2

Berapa kali 3 masuk ke dalam 24? 36 = 18 (dalam desimal). Dalam oktal, 18 desimal = 22_8. Jadi, 3 masuk ke 24_8 sebanyak 6 kali. Langkah 3: Tulis 6 di atas garis sebagai kuosien.

Langkah 4: Kalikan 6_8 dengan 3_8 = 22_

8. Langkah 5

Kurangkan 24_8 – 22_8 = 2_

8. Langkah 6

Karena tidak ada digit tersisa, hasil akhirnya adalah 6_8 dengan sisa 0. Jadi, 24_8 / 3_8 = 6_8“`

Mari kita bedah cara menghitung bilangan oktal, dimulai dari pemahaman dasar sistem bilangan berbasis delapan. Proses konversi ini, seperti halnya banyak aspek lain, sangat penting dalam dunia Pendidikan , karena membantu siswa memahami konsep-konsep matematika dan komputasi secara lebih mendalam. Pemahaman ini membuka wawasan baru, mulai dari representasi bilangan hingga aplikasi dalam pemrograman. Kembali ke oktal, menguasai konversi bilangan ini membuka pintu ke pemahaman yang lebih baik tentang sistem digital.

Contoh 2: Pembagian dengan sisa (35_8 / 4_8)

“““ 35_8 / 4_8 = ? Langkah 1: Bagi 3 (digit pertama dari 35_8) dengan 4. Karena 4 lebih besar dari 3, kita pertimbangkan

35. Langkah 2

Berapa kali 4 masuk ke dalam 35? 47 = 28 (dalam desimal). Dalam oktal, 28 desimal = 34_8. Jadi, 4 masuk ke 35_8 sebanyak 7 kali. Langkah 3: Tulis 7 di atas garis sebagai kuosien.

Langkah 4: Kalikan 7_8 dengan 4_8 = 34_

8. Langkah 5

Kurangkan 35_8 – 34_8 = 1_

8. Langkah 6

Karena tidak ada digit tersisa, hasil akhirnya adalah 7_8 dengan sisa 1. Jadi, 35_8 / 4_8 = 7_8 sisa 1_8“`

Contoh 3: Pembagian dengan bilangan oktal yang lebih panjang (123_8 / 5_8)

“““ 123_8 / 5_8 = ? Langkah 1: Bagi 1 (digit pertama dari 123_8) dengan 5. Karena 5 lebih besar dari 1, kita pertimbangkan

Mari kita mulai dengan bilangan oktal, sistem yang menggunakan basis 8. Konsep ini mungkin terasa rumit, tetapi sebenarnya mirip dengan cara kita menghitung dalam sistem desimal. Namun, ketika kunci pintu Anda macet, apakah Anda akan langsung memikirkan oktal? Tentu tidak! Justru, Anda akan mencari solusi praktis, seperti yang dijelaskan di cara memperbaiki kunci pintu yang macet. Kembali ke oktal, memahami konversi bilangan ini adalah kunci untuk berbagai aplikasi, mulai dari pemrograman hingga sistem digital.

12. Langkah 2

Berapa kali 5 masuk ke dalam 12? 52 = 10 (dalam desimal). Dalam oktal, 10 desimal = 12_8. Jadi, 5 masuk ke 12_8 sebanyak 2 kali. Langkah 3: Tulis 2 di atas garis sebagai kuosien.

Langkah 4: Kalikan 2_8 dengan 5_8 = 12_

8. Langkah 5

Kurangkan 12_8 – 12_8 = 0. Turunkan

3. Langkah 6

Bagi 3 dengan 5. Karena 5 lebih besar dari 3, maka 5 masuk ke dalam 3 sebanyak 0 kali. Tulis 0 di samping 2 di kuosien. Langkah 7: Kalikan 0_8 dengan 5_8 = 0_

8. Langkah 8

Kurangkan 3_8 – 0_8 = 3_

8. Langkah 9

Karena tidak ada digit tersisa, hasil akhirnya adalah 20_8 dengan sisa 3. Jadi, 123_8 / 5_8 = 20_8 sisa 3_8“`

Penanganan Sisa dalam Pembagian Oktal

Sisa (remainder) dalam pembagian oktal diinterpretasikan sama seperti dalam pembagian desimal: ini adalah jumlah yang “tersisa” setelah pembagian selesai. Sisa selalu lebih kecil dari pembagi. Dalam oktal, sisa juga dinyatakan dalam basis 8, yang berarti sisa hanya dapat berupa angka 0 hingga 7. Penting untuk diingat bahwa sisa tidak dikonversi ke desimal; ia tetap dalam format oktal.

Contoh Tambahan:

“““ 47_8 / 6_8 = ? Langkah 1: Berapa kali 6 masuk ke dalam 47? 66 = 36 (dalam desimal). Dalam oktal, 36 desimal = 44_8. Jadi, 6 masuk ke 47_8 sebanyak 6 kali.

Langkah 2: Tulis 6 di atas garis sebagai kuosien. Langkah 3: Kalikan 6_8 dengan 6_8 = 44_

8. Langkah 4

Kurangkan 47_8 – 44_8 = 3_

8. Langkah 5

Karena tidak ada digit tersisa, hasil akhirnya adalah 6_8 dengan sisa 3_8. Jadi, 47_8 / 6_8 = 6_8 sisa 3_8“`

Dalam contoh ini, sisa adalah 3_8, yang lebih kecil dari pembagi 6_8, yang menunjukkan bahwa perhitungan telah dilakukan dengan benar.

Diagram Alir Proses Pembagian Oktal

Diagram alir berikut menggambarkan langkah-langkah pembagian oktal:

Diagram alir untuk pembagian oktal dapat divisualisasikan sebagai berikut (Karena keterbatasan format HTML, deskripsi rinci langkah-langkah akan diberikan sebagai pengganti gambar diagram alir):

Mulai
Input: Dividend (bilangan yang dibagi) dan Divisor (pembagi) dalam oktal.
Inisialisasi: Kuosien (hasil bagi) = 0, Sisa = 0.
Ambil digit paling kiri dari dividend.
Apakah digit atau bagian dari dividend >= divisor?
- Ya: Hitung berapa kali divisor masuk ke dalam bagian dividend saat ini. Tuliskan hasilnya (kuosien sementara) di atas. Kalikan kuosien sementara dengan divisor. Kurangkan hasil perkalian dari bagian dividend. Sisa sementara adalah hasil pengurangan.
- Tidak: Jika ada digit di sebelah kanan, turunkan digit tersebut ke samping sisa. Jika tidak ada digit tersisa, maka sisa adalah sisa akhir.
Apakah ada digit yang belum diproses di dividend?
- Ya: Ulangi langkah 5.
- Tidak: Sisa menjadi sisa akhir.
Hasil Akhir: Tampilkan Kuosien dan Sisa (keduanya dalam oktal).
Selesai

Penjelasan Singkat untuk Setiap Langkah:

Input: Memasukkan bilangan yang akan dibagi dan pembagi dalam sistem oktal.
Inisialisasi: Mengatur nilai awal untuk hasil bagi dan sisa menjadi nol.
Perbandingan: Membandingkan bagian dari bilangan yang dibagi dengan pembagi.
Perhitungan: Melakukan pembagian dan pengurangan untuk menemukan hasil bagi sementara dan sisa sementara.
Iterasi: Mengulangi proses hingga semua digit telah diproses.
Output: Menampilkan hasil bagi akhir dan sisa akhir dalam sistem oktal.

Penggunaan Tabel untuk Ilustrasi

Tabel berikut membandingkan pembagian oktal dengan pembagian desimal, serta menunjukkan bagaimana sisa dihitung:

Bilangan Oktal	Desimal yang Setara	Langkah-Langkah Pembagian	Hasil Akhir
24_8 / 3_8	20 / 3	63 = 18 (22_8). 24_8 – 22_8 = 2.	6_8 sisa 0
35_8 / 4_8	29 / 4	74 = 28 (34_8). 35_8 – 34_8 = 1.	7_8 sisa 1_8
47_8 / 6_8	39 / 6	66 = 36 (44_8). 47_8 – 44_8 = 3.	6_8 sisa 3_8

Tabel ini membantu memvisualisasikan bagaimana proses pembagian oktal dilakukan, dengan menunjukkan padanan desimal untuk memudahkan pemahaman.

Soal Latihan Tambahan

Berikut adalah tiga soal latihan tambahan untuk menguji pemahaman Anda:

56_8 / 2_8 = ?
73_8 / 5_8 = ?
145_8 / 6_8 = ?

Kunci Jawaban:

56_8 / 2_8 = 27_8
73_8 / 5_8 = 13_8 sisa 6_8
145_8 / 6_8 = 20_8 sisa 1_8

Penggunaan Bilangan Oktal dalam Komputasi

Bilangan oktal, meskipun mungkin tidak sepopuler bilangan desimal atau heksadesimal dalam komputasi modern, memiliki peran penting dalam sejarah dan beberapa aplikasi khusus. Penggunaannya menawarkan cara yang efisien untuk merepresentasikan data biner, terutama dalam konteks sistem yang lebih tua atau dalam situasi di mana kebutuhan akan representasi yang ringkas dan mudah dibaca sangat penting. Mari kita telusuri lebih dalam bagaimana bilangan oktal dimanfaatkan dalam dunia komputasi.

Aplikasi Bilangan Oktal dalam Komputasi

Bilangan oktal menemukan aplikasi di berbagai bidang komputasi, meskipun popularitasnya telah menurun seiring waktu. Penerapannya yang paling menonjol terletak pada representasi izin akses file dalam sistem operasi berbasis Unix dan turunannya. Selain itu, oktal juga digunakan dalam beberapa konteks lain, terutama dalam sistem yang beroperasi pada tingkat yang lebih rendah.

Alasan Penggunaan Bilangan Oktal dalam Beberapa Sistem

Penggunaan bilangan oktal dalam beberapa sistem didasarkan pada beberapa alasan utama. Pertama, oktal menyediakan cara yang lebih ringkas untuk merepresentasikan data biner dibandingkan dengan desimal. Kedua, oktal memiliki hubungan yang mudah dengan biner, di mana setiap digit oktal dapat dengan mudah diwakili oleh tiga bit biner. Ketiga, oktal menawarkan cara yang lebih mudah dibaca daripada representasi biner panjang, yang penting untuk debugging dan pemahaman kode.

Contoh Sistem atau Perangkat Keras yang Menggunakan Bilangan Oktal

Meskipun penggunaannya telah berkurang, bilangan oktal masih dapat ditemukan dalam beberapa sistem dan perangkat keras. Contohnya meliputi:

Sistem Operasi Berbasis Unix: Seperti yang telah disebutkan, sistem operasi seperti Linux dan macOS menggunakan oktal untuk merepresentasikan izin akses file. Setiap digit oktal mewakili izin untuk pemilik, grup, dan pengguna lain (misalnya, membaca, menulis, dan mengeksekusi).
Sistem Embedded: Dalam beberapa sistem embedded yang lebih tua, oktal digunakan untuk representasi data dan alamat memori karena kemudahan konversinya dengan biner.
Representasi Izin File: Penggunaan oktal dalam representasi izin file Unix adalah contoh klasik. Angka oktal digunakan untuk menentukan hak akses ke file dan direktori, seperti membaca, menulis, dan mengeksekusi. Misalnya, izin 755 berarti pemilik memiliki akses membaca, menulis, dan mengeksekusi, sementara grup dan pengguna lain hanya memiliki akses membaca dan mengeksekusi.

Kelebihan dan Kekurangan Penggunaan Oktal

Penggunaan bilangan oktal dalam komputasi memiliki kelebihan dan kekurangan. Memahami aspek-aspek ini penting untuk menilai relevansinya dalam konteks tertentu.

Kelebihan:
- Representasi Ringkas: Oktal menawarkan representasi yang lebih ringkas daripada biner, terutama untuk data yang panjang.
- Mudah Dikonversi ke Biner: Konversi antara oktal dan biner sangat mudah, yang mempermudah pemahaman dan manipulasi data.
- Pembacaan yang Lebih Baik: Oktal lebih mudah dibaca daripada biner, terutama dalam konteks debugging dan analisis kode.
- Representasi Izin File: Penggunaan dalam izin file Unix adalah contoh yang sangat baik dari kegunaan praktis.
Kekurangan:
- Tidak Se-Populer Heksadesimal: Heksadesimal lebih populer dalam komputasi modern karena lebih mudah dikonversi ke biner dan lebih ringkas.
- Keterbatasan dalam Beberapa Aplikasi: Dalam beberapa aplikasi, oktal mungkin tidak seefisien heksadesimal dalam representasi data.
- Penggunaan Terbatas dalam Perangkat Keras Modern: Seiring perkembangan teknologi, penggunaan oktal dalam perangkat keras modern semakin terbatas.

Perbandingan dengan Sistem Bilangan Lain

Sistem bilangan oktal, biner, desimal, dan heksadesimal merupakan fondasi penting dalam dunia komputasi. Memahami perbedaan dan kelebihan masing-masing sistem sangat krusial untuk mengoptimalkan representasi data dan efisiensi perhitungan. Mari kita telusuri perbandingan mendalam antara sistem-sistem ini, menyoroti keunggulan dan kelemahannya dalam berbagai konteks.

Perbandingan dengan Bilangan Biner dan Heksadesimal

Bilangan oktal sering kali dibandingkan dengan biner dan heksadesimal karena ketiganya digunakan dalam representasi data digital. Biner adalah sistem dasar dalam komputasi, sementara oktal dan heksadesimal digunakan untuk menyederhanakan representasi biner yang panjang. Heksadesimal, khususnya, lebih populer karena lebih ringkas. Mari kita lihat perbedaan utama:

Basis Bilangan: Biner menggunakan basis 2 (0 dan 1), oktal menggunakan basis 8 (0-7), dan heksadesimal menggunakan basis 16 (0-9 dan A-F). Desimal menggunakan basis 10 (0-9).
Kepadatan Representasi: Heksadesimal menawarkan kepadatan representasi tertinggi, memungkinkan representasi data yang lebih ringkas dibandingkan oktal dan biner. Oktal lebih ringkas daripada biner, namun kurang efisien dibandingkan heksadesimal.
Kemudahan Konversi: Konversi antara biner dan oktal relatif mudah karena 8 adalah pangkat dari 2 (2 ³ = 8). Konversi antara biner dan heksadesimal juga mudah karena 16 adalah pangkat dari 2 (2 ⁴ = 16). Konversi ke desimal melibatkan perhitungan berdasarkan nilai posisi digit.
Penggunaan dalam Komputasi: Biner adalah bahasa dasar komputer. Oktal digunakan dalam beberapa sistem operasi dan pengaturan hak akses file, sementara heksadesimal umum digunakan dalam representasi warna, alamat memori, dan debugging.

Keuntungan dan Kerugian Menggunakan Oktal

Penggunaan sistem oktal memiliki kelebihan dan kekurangan yang perlu dipertimbangkan. Memahami aspek-aspek ini membantu dalam memilih sistem bilangan yang paling sesuai untuk situasi tertentu.

Keuntungan:
- Penyederhanaan Biner: Oktal menyederhanakan representasi biner, terutama pada masa-masa awal komputasi ketika layar dan penyimpanan data memiliki keterbatasan. Mengelompokkan bit biner menjadi oktal membuat data lebih mudah dibaca dan dipahami oleh manusia.
- Konversi Mudah: Konversi antara biner dan oktal relatif sederhana, yang mengurangi kompleksitas perhitungan.
- Penggunaan dalam Sistem Unix/Linux: Oktal digunakan dalam pengaturan hak akses file (permissions) pada sistem operasi Unix/Linux.
Kerugian:
- Kepadatan Representasi Lebih Rendah dari Heksadesimal: Dibandingkan dengan heksadesimal, oktal memerlukan lebih banyak digit untuk merepresentasikan nilai yang sama, yang mengurangi efisiensi dalam penyimpanan dan transmisi data.
- Kurang Populer: Heksadesimal telah menggantikan oktal dalam banyak aplikasi karena kepadatan representasinya yang lebih baik dan penggunaan yang lebih luas dalam berbagai teknologi.

Tabel Perbandingan Representasi Bilangan, Cara menghitung bilangan oktal

Tabel berikut memberikan perbandingan representasi bilangan yang sama dalam sistem biner, oktal, desimal, dan heksadesimal. Hal ini memberikan gambaran yang jelas tentang perbedaan dalam representasi nilai yang sama menggunakan sistem bilangan yang berbeda.

Biner	Oktal	Desimal	Heksadesimal
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

Contoh Soal Latihan Konversi

Setelah memahami konsep dasar konversi bilangan oktal, saatnya menguji pemahaman Anda melalui latihan soal. Berikut adalah beberapa contoh soal yang mencakup berbagai jenis konversi, mulai dari desimal ke oktal, oktal ke desimal, biner ke oktal, hingga oktal ke biner. Kerjakan soal-soal ini untuk mengasah kemampuan Anda dalam mengolah sistem bilangan oktal.

Konversi Desimal ke Oktal

Latihan pertama berfokus pada konversi bilangan desimal ke oktal. Ingatlah bahwa Anda perlu membagi bilangan desimal dengan 8 secara berulang hingga hasil bagi menjadi 0, kemudian kumpulkan sisa pembagian dari bawah ke atas.

Soal 1: Konversikan bilangan desimal 25 ke oktal.
Soal 2: Konversikan bilangan desimal 100 ke oktal.
Soal 3: Konversikan bilangan desimal 378 ke oktal.

Konversi Oktal ke Desimal

Selanjutnya, kita akan berlatih konversi bilangan oktal ke desimal. Prosesnya melibatkan perkalian setiap digit oktal dengan pangkat 8 yang sesuai, dimulai dari kanan (digit paling kanan dikalikan dengan 8 ⁰).

Soal 1: Konversikan bilangan oktal 32 ke desimal.
Soal 2: Konversikan bilangan oktal 157 ke desimal.
Soal 3: Konversikan bilangan oktal 700 ke desimal.

Konversi Biner ke Oktal

Konversi biner ke oktal dilakukan dengan mengelompokkan digit biner menjadi kelompok-kelompok yang terdiri dari tiga digit, dimulai dari kanan. Setiap kelompok tiga digit biner kemudian dikonversi menjadi satu digit oktal.

Soal 1: Konversikan bilangan biner 110101 ke oktal.
Soal 2: Konversikan bilangan biner 101110010 ke oktal.
Soal 3: Konversikan bilangan biner 1110001011 ke oktal.

Konversi Oktal ke Biner

Terakhir, kita akan berlatih konversi oktal ke biner. Prosesnya adalah kebalikan dari konversi biner ke oktal. Setiap digit oktal dikonversi menjadi tiga digit biner.

Soal 1: Konversikan bilangan oktal 52 ke biner.
Soal 2: Konversikan bilangan oktal 276 ke biner.
Soal 3: Konversikan bilangan oktal 1034 ke biner.

Contoh Soal Latihan Aritmatika

Setelah memahami konsep dasar dan berbagai metode perhitungan bilangan oktal, saatnya menguji pemahaman Anda melalui serangkaian soal latihan. Latihan ini dirancang untuk memperdalam kemampuan Anda dalam melakukan operasi aritmatika dasar pada bilangan oktal. Soal-soal ini mencakup penjumlahan, pengurangan, perkalian, dan pembagian. Pastikan untuk mengerjakan soal-soal ini dengan teliti dan periksa kembali jawaban Anda untuk memastikan keakuratannya.

Soal Latihan Penjumlahan Bilangan Oktal

Penjumlahan bilangan oktal mengikuti prinsip yang sama dengan penjumlahan desimal, namun dengan basis
8. Jika hasil penjumlahan melebihi 7, lakukan ‘carry-over’ ke digit berikutnya. Berikut adalah beberapa contoh soal latihan:

Soal 1: 12 ₈ + 34 ₈ = ?
Soal 2: 25 ₈ + 13 ₈ = ?
Soal 3: 76 ₈ + 11 ₈ = ?
Soal 4: 32 ₈ + 45 ₈ = ?
Soal 5: 17 ₈ + 26 ₈ = ?

Petunjuk: Kerjakan soal-soal ini dengan menjumlahkan setiap kolom digit, dimulai dari kanan. Jika jumlahnya lebih besar dari 7, bagi dengan 8, sisa adalah digit pada kolom tersebut, dan hasil bagi adalah ‘carry-over’ ke kolom berikutnya.

Soal Latihan Pengurangan Bilangan Oktal

Pengurangan bilangan oktal juga mengikuti prinsip yang serupa dengan pengurangan desimal. Jika digit yang akan dikurangi lebih besar dari digit yang dikurangi, lakukan ‘borrow’ dari digit di sebelah kiri. Berikut adalah beberapa contoh soal latihan:

Soal 1: 45 ₈
-12 ₈ = ?
Soal 2: 67 ₈
-23 ₈ = ?
Soal 3: 34 ₈
-15 ₈ = ?
Soal 4: 51 ₈
-26 ₈ = ?
Soal 5: 70 ₈
-34 ₈ = ?

Petunjuk: Kerjakan soal-soal ini dengan mengurangkan setiap kolom digit, dimulai dari kanan. Jika digit yang dikurangi lebih kecil dari digit yang akan dikurangi, pinjam 8 dari digit di sebelah kiri.

Soal Latihan Perkalian Bilangan Oktal

Perkalian bilangan oktal juga mengikuti prinsip yang sama dengan perkalian desimal, namun dengan basis
8. Hasil perkalian harus dikonversi ke oktal, dan jika perlu, lakukan ‘carry-over’. Berikut adalah beberapa contoh soal latihan:

Soal 1: 12 ₈ × 3 ₈ = ?
Soal 2: 23 ₈ × 4 ₈ = ?
Soal 3: 15 ₈ × 5 ₈ = ?
Soal 4: 21 ₈ × 6 ₈ = ?
Soal 5: 34 ₈ × 2 ₈ = ?

Petunjuk: Kalikan setiap digit, dan konversikan hasilnya ke oktal. Jika hasil perkalian melebihi 7, lakukan ‘carry-over’ ke digit berikutnya.

Soal Latihan Pembagian Bilangan Oktal

Pembagian bilangan oktal mirip dengan pembagian desimal. Prosesnya melibatkan pembagian berulang, dengan memperhatikan sisa pembagian dalam basis
8. Berikut adalah beberapa contoh soal latihan:

Soal 1: 44 ₈ ÷ 2 ₈ = ?
Soal 2: 62 ₈ ÷ 3 ₈ = ?
Soal 3: 71 ₈ ÷ 5 ₈ = ?
Soal 4: 123 ₈ ÷ 7 ₈ = ?
Soal 5: 144 ₈ ÷ 6 ₈ = ?

Petunjuk: Lakukan pembagian seperti biasa, namun pastikan untuk memperhatikan sisa pembagian dalam basis 8.

Tips dan Trik dalam Perhitungan Oktal

Source: slidesharecdn.com

Memahami dan menguasai perhitungan oktal sangat penting dalam berbagai bidang, terutama dalam ilmu komputer dan rekayasa digital. Artikel ini akan membahas berbagai tips dan trik untuk mempermudah perhitungan oktal, menghindari kesalahan umum, dan menyediakan sumber daya tambahan untuk memperdalam pengetahuan Anda. Mari kita selami lebih dalam!

Dalam perhitungan oktal, setiap digit mewakili nilai kelipatan dari delapan. Sistem ini menggunakan basis 8, yang berarti hanya ada delapan simbol yang valid: 0, 1, 2, 3, 4, 5, 6, dan 7. Memahami dasar-dasar ini adalah kunci untuk menguasai perhitungan oktal.

Tips untuk Mempermudah Perhitungan Oktal

Berikut adalah beberapa tips yang terstruktur dan mudah diikuti untuk mempermudah perhitungan oktal, baik dalam penjumlahan, pengurangan, perkalian, pembagian, maupun konversi:

Penjumlahan Oktal:
Penjumlahan oktal mirip dengan penjumlahan desimal, tetapi dengan basis 8. Jika hasil penjumlahan dua digit lebih besar dari 7, lakukan pengurangan dengan 8 dan bawa 1 ke kolom berikutnya.

Contoh:
- Soal: 35 ₈ + 27 ₈
- Solusi:
  - Tambahkan kolom paling kanan: 5 + 7 = 12. Karena 12 lebih besar dari 7, kurangi 8 (12 – 8 = 4) dan bawa 1 ke kolom berikutnya.
  - Tambahkan kolom berikutnya: 3 + 2 + 1 (dari bawaan) = 6.
  - Hasil: 64 ₈
Pengurangan Oktal:
Pengurangan oktal juga mirip dengan pengurangan desimal. Jika digit yang dikurangi lebih besar dari digit yang akan dikurangi, pinjam 8 dari kolom berikutnya.

Contoh:
- Soal: 62 ₈
  -15 ₈
- Solusi:
  - Kurangkan kolom paling kanan: 2 – 5. Karena 2 lebih kecil dari 5, pinjam 8 dari kolom berikutnya (menjadi 2 + 8 = 10). 10 – 5 = 5.
  - Kurangkan kolom berikutnya: 6 (telah dipinjam 1) menjadi 5. 5 – 1 = 4.
  - Hasil: 45 ₈
Perkalian Oktal:
Perkalian oktal melibatkan perkalian seperti biasa, tetapi dengan mempertimbangkan basis 8. Jika hasil perkalian lebih besar dari 7, ubah ke dalam oktal (bagi dengan 8, sisa adalah digit, hasil bagi adalah bawaan).

Contoh:
- Soal: 23 ₈
  – 4 ₈
- Solusi:
  - Kalikan: 4
    – 3 =
    12. Ubah 12 ke oktal: 12 / 8 = 1 sisa 4. Tulis 4, bawa 1.
  - Kalikan: 4
    – 2 =
    8. Tambahkan bawaan 1: 8 + 1 =
    9. Ubah 9 ke oktal: 9 / 8 = 1 sisa 1. Tulis 11.
  - Hasil: 114 ₈
Pembagian Oktal:
Pembagian oktal juga mengikuti prinsip yang sama dengan pembagian desimal, tetapi dengan basis 8. Gunakan perkalian dan pengurangan oktal untuk menyelesaikan pembagian.

Contoh:
- Soal: 64 ₈ / 2 ₈
- Solusi:
  - Bagi 6 dengan 2: 6 / 2 = 3. Tulis 3 di hasil.
  - Kalikan 3 dengan 2: 3
    – 2 = 6. Kurangkan 6 dari 6 = 0.
  - Turunkan
    4. Bagi 4 dengan 2: 4 / 2 = 2. Tulis 2 di hasil.
  - Kalikan 2 dengan 2: 2
    – 2 = 4. Kurangkan 4 dari 4 = 0.
  - Hasil: 32 ₈
Konversi Desimal ke Oktal:
Untuk mengkonversi desimal ke oktal, bagi bilangan desimal dengan 8 berulang kali. Sisa dari setiap pembagian adalah digit oktal, dimulai dari digit paling kanan. Baca sisa dari bawah ke atas.

Contoh:
- Soal: Konversikan 45 ₁₀ ke oktal.
- Solusi:
  - 45 / 8 = 5 sisa 5
  - 5 / 8 = 0 sisa 5
  - Baca sisa dari bawah ke atas: 55 ₈
Konversi Oktal ke Desimal:
Untuk mengkonversi oktal ke desimal, kalikan setiap digit oktal dengan pangkat 8 yang sesuai (dimulai dari 0 dari kanan), kemudian jumlahkan hasilnya.

Contoh:
- Soal: Konversikan 55 ₈ ke desimal.
- Solusi:
  - (5
    – 8 ¹) + (5
    – 8 ⁰) = 40 + 5 = 45 ₁₀
Konversi Biner ke Oktal:
Kelompokkan digit biner menjadi kelompok tiga digit, mulai dari kanan. Konversikan setiap kelompok tiga digit biner menjadi digit oktal yang sesuai.

Contoh:
- Soal: Konversikan 110101 ₂ ke oktal.
- Solusi:
  - Kelompokkan: 110 101
  - Konversikan: 110 = 6, 101 = 5
  - Hasil: 65 ₈
Konversi Oktal ke Biner:
Konversikan setiap digit oktal menjadi tiga digit biner yang sesuai.

Contoh:
- Soal: Konversikan 73 ₈ ke biner.
- Solusi:
  - 7 = 111, 3 = 011
  - Hasil: 111011 ₂

Trik untuk Menghindari Kesalahan Umum dalam Perhitungan Oktal

Kesalahan dalam perhitungan oktal sering terjadi karena kurangnya pemahaman tentang basis
8. Berikut adalah beberapa kesalahan umum dan cara menghindarinya:

Kesalahan: Lupa Membawa atau Meminjam
Kesalahan ini sering terjadi dalam penjumlahan dan pengurangan. Misalnya, saat menjumlahkan 6 + 5, seringkali hanya ditulis 11, bukan 13 ₈ (karena 6 + 5 = 11, dan 11 – 8 = 3, bawa 1).

Contoh: 56₈ + 24 ₈ = 80 ₈ (Salah)

Pencegahan: Selalu ingat untuk mengurangkan 8 dan membawa 1 jika hasil penjumlahan lebih besar dari 7. Pastikan untuk menambahkan angka bawaan ke kolom berikutnya.

Solusi yang benar: 56₈ + 24 ₈ = 102 ₈
Kesalahan: Kesalahan dalam Konversi ke Desimal
Kesalahan ini sering terjadi saat mengkonversi oktal ke desimal. Misalnya, mengalikan digit dengan pangkat 10, bukan 8.

Contoh: 23₈ = (2
– 10 ¹) + (3
– 10 ⁰) = 23 ₁₀ (Salah)

Pencegahan: Selalu gunakan pangkat 8. Ingat bahwa posisi digit dari kanan ke kiri adalah 8 ⁰, 8 ¹, 8 ², dst.

Mari kita mulai dengan dunia bilangan oktal. Konsepnya sederhana, hanya menggunakan basis delapan. Tapi, bagaimana jika kita bisa mengalihkan fokus sejenak? Pernahkah terpikir bagaimana cara mendapatkan tambahan dana secara gratis? Tentu saja! Ada banyak cara, bahkan beberapa di antaranya bisa kamu temukan di artikel yang membahas cara dapat uang dana gratis.

Kembali ke oktal, pemahaman yang baik akan membantu dalam berbagai aspek komputasi, jadi teruslah belajar dan eksplorasi!

Solusi yang benar: 23₈ = (2
– 8 ¹) + (3
– 8 ⁰) = 16 + 3 = 19 ₁₀
Kesalahan: Kesalahan dalam Konversi dari Biner ke Oktal
Kesalahan ini biasanya terjadi saat salah mengelompokkan digit biner. Misalnya, mengelompokkan digit dari kiri ke kanan, bukan dari kanan ke kiri.

Contoh: 101100₂ -> 101 100 = 54 ₈ (Salah)

Pencegahan: Selalu kelompokkan digit biner dari kanan ke kiri, dalam kelompok tiga digit.

Solusi yang benar: 101100₂ -> 101 100 = 54 ₈
Kesalahan: Kesalahan dalam Konversi dari Oktal ke Biner
Kesalahan ini sering terjadi saat salah mengkonversi digit oktal ke biner. Misalnya, salah mengkonversi 7 menjadi 100 (seharusnya 111).

Contoh: 73₈ = 100011 ₂ (Salah)

Pencegahan: Pastikan untuk mengkonversi setiap digit oktal ke tiga digit biner yang benar. Gunakan tabel konversi jika perlu.

Solusi yang benar: 73₈ = 111011 ₂
Kesalahan: Salah Menggunakan Operasi Aritmatika
Kesalahan ini melibatkan penggunaan operasi aritmatika yang salah saat melakukan perhitungan. Misalnya, saat melakukan perkalian, tidak mengkonversi hasil perkalian yang lebih besar dari 7 ke dalam bentuk oktal yang benar.

Contoh: 4₈
– 3 ₈ = 12 ₈ (Salah)

Pencegahan: Ingat untuk selalu mempertimbangkan basis 8 saat melakukan operasi aritmatika. Gunakan konversi oktal jika hasil operasi melebihi 7.

Solusi yang benar: 4₈
– 3 ₈ = 14 ₈ (karena 12 dalam desimal adalah 14 dalam oktal)

Sumber Daya Tambahan untuk Mempelajari Bilangan Oktal

Untuk memperdalam pemahaman Anda tentang bilangan oktal, berikut adalah beberapa sumber daya tambahan:

Jenis Sumber Daya	Deskripsi	Tautan
Situs Web	Menyediakan penjelasan komprehensif tentang sistem bilangan oktal, konversi, dan aritmatika.	Tutorialspoint – Octal Number System
Video Tutorial	Tutorial video langkah demi langkah tentang penjumlahan, pengurangan, perkalian, dan pembagian bilangan oktal.	YouTube – Octal Number System Explained
Forum Diskusi	Tempat untuk bertanya dan berdiskusi tentang perhitungan oktal, serta berbagi tips dan trik.	Physics Forums – Computer Science
Buku	Referensi buku teks yang membahas sistem bilangan oktal secara mendalam, dengan contoh soal dan latihan.	Digital Design and Computer Architecture oleh David Harris dan Sarah Harris

Infografis Ringkasan

Berikut adalah contoh visual yang merangkum tips dan trik penting dalam perhitungan oktal. Infografis ini mencakup tips utama untuk setiap operasi aritmatika, ilustrasi visual untuk membantu memahami konsep, dan peringatan tentang kesalahan umum yang harus dihindari. Infografis ini dirancang untuk memudahkan pemahaman dan membantu dalam mengingat konsep-konsep penting.

Infografis:

Infografis ini akan menampilkan diagram yang berisi:

Penjumlahan: Ilustrasi penjumlahan dua bilangan oktal dengan membawa.
Pengurangan: Ilustrasi pengurangan dua bilangan oktal dengan meminjam.
Perkalian: Ilustrasi perkalian dua bilangan oktal dengan konversi ke oktal.
Pembagian: Ilustrasi pembagian dua bilangan oktal dengan langkah-langkah.
Konversi: Diagram konversi dari desimal ke oktal, oktal ke desimal, biner ke oktal, dan oktal ke biner.
Kesalahan Umum: Daftar kesalahan umum yang harus dihindari, seperti lupa membawa atau meminjam, dan kesalahan dalam konversi.

Semua operasi akan diilustrasikan dengan contoh soal dan solusi yang jelas.

Akhir Kata: Cara Menghitung Bilangan Oktal

Dari representasi data yang efisien hingga aplikasi praktis dalam sistem digital, bilangan oktal telah meninggalkan jejak yang signifikan dalam sejarah komputasi. Meskipun heksadesimal kini lebih umum, pemahaman tentang oktal tetap berharga. Dengan menguasai konsep-konsep yang telah dibahas, Anda telah membuka pintu ke pemahaman yang lebih dalam tentang bagaimana komputer bekerja.

Teruslah menjelajahi dunia sistem bilangan, karena pengetahuan ini adalah fondasi penting dalam perjalanan Anda di dunia teknologi.

Pertanyaan dan Jawaban

Apa itu sistem bilangan oktal?

Sistem bilangan oktal adalah sistem bilangan berbasis delapan, menggunakan digit 0 hingga 7 untuk merepresentasikan nilai.

Mengapa oktal digunakan dalam komputasi?

Oktal digunakan untuk representasi data yang lebih ringkas daripada biner, terutama dalam memori komputer, dan juga terkait erat dengan biner.

Bagaimana cara mengkonversi desimal ke oktal?

Konversi desimal ke oktal dilakukan dengan membagi angka desimal berulang kali dengan 8 dan mencatat sisa pembagiannya, kemudian mengumpulkan sisa dari bawah ke atas.

Bagaimana cara mengkonversi biner ke oktal?

Konversi biner ke oktal dilakukan dengan mengelompokkan digit biner menjadi grup tiga digit, dimulai dari kanan, dan kemudian mengkonversi setiap grup ke digit oktal yang sesuai.