Pernahkah Anda bertanya-tanya bagaimana akar kuadrat yang tampak rumit bisa disederhanakan? Mari kita selami dunia matematika yang menarik ini, di mana ‘cara mengubah akar menjadi pangkat’ menjadi kunci untuk membuka berbagai konsep. Bayangkan akar sebagai teka-teki yang menantang, dan pangkat sebagai kunci untuk memecahkannya. Dalam artikel ini, kita akan membahas langkah demi langkah bagaimana mengubah akar menjadi pangkat, membuka potensi baru dalam memecahkan masalah matematika.
Dari akar kuadrat sederhana hingga akar pangkat tiga dan lebih tinggi, kita akan menjelajahi bagaimana mengubahnya menjadi bentuk pangkat pecahan. Kami akan membahas konsep dasar, langkah-langkah konversi detail, penanganan variabel, dan contoh soal dengan solusi lengkap. Kita juga akan melihat bagaimana konsep ini diterapkan dalam berbagai bidang, mulai dari aljabar hingga fisika, serta memberikan tips untuk menghindari kesalahan umum. Siap untuk mengubah cara pandang Anda terhadap akar dan pangkat?
Pemahaman Dasar Konsep Akar dan Pangkat
Akar dan pangkat adalah dua konsep fundamental dalam matematika yang saling berkaitan erat. Keduanya merupakan operasi matematika yang digunakan untuk memanipulasi angka dan variabel. Memahami perbedaan dan hubungan antara akar dan pangkat sangat penting untuk menguasai berbagai konsep matematika lainnya, mulai dari aljabar dasar hingga kalkulus. Artikel ini akan membahas secara mendalam mengenai konsep akar dan pangkat, meliputi definisi, contoh, aplikasi, dan kesalahan umum yang sering terjadi.
Perbedaan Mendasar antara Akar dan Pangkat
Akar dan pangkat adalah operasi matematika yang saling berlawanan (invers). Pangkat (atau eksponen) menunjukkan berapa kali suatu bilangan (basis) dikalikan dengan dirinya sendiri. Sementara itu, akar adalah operasi untuk menemukan bilangan yang, jika dipangkatkan, akan menghasilkan bilangan tertentu. Perbedaan utama terletak pada arah operasi: pangkat “mengembangkan” bilangan, sedangkan akar “menguraikan” bilangan kembali ke bentuk aslinya (sebelum dipangkatkan).
Sebagai contoh:
- Pangkat: 2 3 = 2 × 2 × 2 = 8 (2 dipangkatkan 3 menghasilkan 8)
- Akar: √8 = 2 (akar pangkat tiga dari 8 adalah 2, karena 2 3 = 8)
Fungsi utama pangkat adalah untuk menyederhanakan penulisan perkalian berulang. Fungsi utama akar adalah untuk menemukan nilai yang menjadi basis dari suatu pangkat.
Hubungan Akar Kuadrat dan Pangkat Dua
Akar kuadrat dan pangkat dua adalah contoh khusus dari hubungan invers antara akar dan pangkat. Pangkat dua (atau kuadrat) dari suatu bilangan adalah bilangan tersebut dikalikan dengan dirinya sendiri. Akar kuadrat adalah operasi yang mencari bilangan yang, jika dikuadratkan, menghasilkan bilangan tertentu.
Contoh:
- Pangkat dua: 3 2 = 3 × 3 = 9
- Akar kuadrat: √9 = 3 (karena 3 2 = 9)
Persamaan matematika yang dapat diselesaikan dengan kedua operasi ini:
- x 2 = 16 (untuk mencari nilai x, kita ambil akar kuadrat dari 16, sehingga x = 4 atau x = -4)
- √x = 5 (untuk mencari nilai x, kita kuadratkan kedua sisi, sehingga x = 25)
Tabel Notasi Akar dan Pangkat
Tabel berikut membandingkan notasi akar dan pangkat, serta bagaimana mereka merepresentasikan operasi matematika yang sama.
| Notasi | Operasi | Contoh |
|---|---|---|
| xn | x dipangkatkan n (x dikalikan dengan dirinya sendiri sebanyak n kali) |
|
| √x atau x1/2 | Akar kuadrat dari x (bilangan yang jika dikuadratkan menghasilkan x) |
|
| n√x atau x1/n | Akar pangkat n dari x (bilangan yang jika dipangkatkan n menghasilkan x) |
|
Ilustrasi Visual Hubungan Akar dan Pangkat
Ilustrasi visual berikut menunjukkan hubungan timbal balik antara akar dan pangkat menggunakan contoh konkret. Perhatikan bagaimana operasi pangkat dan akar saling membatalkan.
Contoh:
Bayangkan sebuah kotak dengan sisi 4 satuan. Luas kotak tersebut adalah 4 2 = 16 satuan persegi. Jika kita ingin mencari panjang sisi kotak tersebut dari luasnya (16), kita menggunakan akar kuadrat: √16 = 4.
Diagram:
Sebuah persegi digambar. Label: Sisi = 4, Luas =
16. Panah bolak-balik menunjukkan hubungan antara sisi dan luas:
- 4 (sisi) → dipangkatkan 2 → 16 (luas)
- 16 (luas) → diakarkan kuadrat → 4 (sisi)
Penjelasan: Diagram ini menunjukkan bahwa operasi pangkat dua (kuadrat) mengubah panjang sisi menjadi luas, sedangkan operasi akar kuadrat mengubah luas kembali menjadi panjang sisi.
Kuis Singkat tentang Akar dan Pangkat
Berikut adalah kuis singkat untuk menguji pemahaman tentang akar dan pangkat.
- Hasil dari 52 adalah?
- 10
- 25
- 125
- 5
Jawaban: b. 25 (5 2 = 5 × 5 = 25)
- √36 sama dengan?
- 6
- 18
- 3
- 12
Jawaban: a. 6 (√36 = 6 karena 6 2 = 36)
- Jika x 2 = 49, maka x adalah?
- 7
- -7
- 7 dan -7
- 49
Jawaban: c. 7 dan -7 (karena 7 2 = 49 dan (-7) 2 = 49)
- Nilai dari 3√27 adalah?
- 3
- 9
- 81
- 6
Jawaban: a. 3 ( 3√27 = 3 karena 3 3 = 27)
- Bentuk sederhana dari (2 3) 2 adalah?
- 25
- 2 6
- 2 8
- 2 9
Jawaban: b. 2 6 ((2 3) 2 = 2 (3*2) = 2 6)
Penerapan Akar dan Pangkat dalam Ilmu Pengetahuan Alam
Konsep akar dan pangkat memiliki aplikasi yang luas dalam berbagai bidang ilmu pengetahuan alam. Contohnya:
- Fisika:
- Dalam perhitungan energi kinetik (KE = 1/2
– mv 2), pangkat dua digunakan untuk menghitung kuadrat kecepatan (v). - Dalam perhitungan jarak tempuh dalam gerak lurus berubah beraturan, akar kuadrat digunakan untuk mencari waktu jika jarak dan percepatan diketahui.
- Dalam perhitungan energi kinetik (KE = 1/2
- Kimia:
- Dalam perhitungan pH dan pOH, logaritma (yang terkait erat dengan pangkat) digunakan untuk menyatakan konsentrasi ion hidrogen dan hidroksida.
- Dalam perhitungan laju reaksi, pangkat digunakan untuk menyatakan orde reaksi terhadap suatu reaktan.
Contoh nyata penggunaan akar dan pangkat dalam perhitungan ilmiah:
Misalnya, dalam fisika, untuk menghitung kecepatan akhir (v) suatu benda yang jatuh bebas, rumus yang digunakan adalah v = √(2gh), di mana g adalah percepatan gravitasi dan h adalah ketinggian. Dalam contoh ini, akar kuadrat digunakan untuk mencari kecepatan.
Cerita Pendek tentang Akar dan Pangkat dalam Kehidupan Sehari-hari
Di sebuah desa yang tenang, hiduplah seorang petani bernama Pak Budi. Pak Budi memiliki sebidang tanah berbentuk persegi. Suatu hari, ia memutuskan untuk memperluas tanahnya. Ia tahu bahwa luas tanah awalnya adalah 100 meter persegi. Ia ingin tahu berapa panjang sisi tanah awalnya.
Dengan pengetahuan matematika sederhana, ia menghitung: √100 = 10 meter. Artinya, sisi tanah awalnya adalah 10 meter.
Kemudian, Pak Budi ingin menggandakan luas tanahnya. Jika luasnya sekarang 200 meter persegi, berapa panjang sisinya? Ia menghitung: √200 ≈ 14.14 meter. Dengan pengetahuan ini, Pak Budi dapat merencanakan perluasan tanahnya dengan lebih efisien. Ia juga menggunakan konsep pangkat saat menghitung kebutuhan bibit tanaman, memperkirakan jumlah pupuk, dan menghitung hasil panen.
Suatu hari, ia ingin membuat pagar di sekeliling tanahnya. Untuk menghitung panjang pagar yang dibutuhkan, ia harus mengalikan panjang sisi dengan jumlah sisi (4 untuk persegi). Ia menggunakan konsep perkalian (yang juga terkait dengan pangkat) untuk mempermudah perhitungan.
Kisah Pak Budi menunjukkan bahwa akar dan pangkat bukan hanya konsep abstrak, tetapi alat yang berguna dalam kehidupan sehari-hari.
Kesalahan Umum dalam Mengerjakan Soal Akar dan Pangkat
Berikut adalah beberapa kesalahan umum yang sering dilakukan siswa saat mengerjakan soal akar dan pangkat, beserta cara mengatasinya:
- Kesalahan: Lupa bahwa akar kuadrat memiliki dua solusi (positif dan negatif).
Cara Mengatasi: Selalu ingat bahwa bilangan positif dan negatif yang dikuadratkan akan menghasilkan nilai positif. Contoh: √9 = ±3
Oke, mari kita bedah dulu konsep akar menjadi pangkat. Ini seperti mengubah bahasa, dari simbol akar yang terlihat rumit menjadi lebih sederhana. Nah, sambil asyik belajar matematika, pernahkah terpikir bagaimana mendapatkan keuntungan dari belanja? Misalnya, dengan memiliki kartu member. Prosesnya ternyata tak serumit mengubah akar, bahkan lebih mudah daripada memahami rumus pangkat! Untuk lebih jelasnya, simak saja cara daftar kartu member alfamart.
Setelah urusan diskon beres, mari kembali ke akar dan pangkat, karena keduanya punya kekuatan yang sama: mengubah bentuk, namun tetap menjaga nilai.
- Kesalahan: Salah mengaplikasikan aturan pangkat.
Cara Mengatasi: Hafalkan dan pahami aturan pangkat (misalnya, x m
– x n = x m+n, (x m) n = x m*n) dan latihan soal secara konsisten. - Kesalahan: Salah menghitung akar dari bilangan negatif.
Cara Mengatasi: Ingat bahwa akar kuadrat dari bilangan negatif tidak memiliki solusi dalam himpunan bilangan real. Gunakan konsep bilangan kompleks jika diperlukan.
- Kesalahan: Salah dalam mengurutkan operasi matematika (urutan operasi).
Cara Mengatasi: Selalu ingat urutan operasi (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (dari kiri ke kanan), Addition and Subtraction (dari kiri ke kanan).
- Kesalahan: Salah dalam menyederhanakan ekspresi yang melibatkan akar.
Cara Mengatasi: Pahami konsep faktor prima dan bagaimana cara menyederhanakan akar dengan mengeluarkan faktor-faktor yang kuadrat sempurna.
Sejarah Perkembangan Akar dan Pangkat
Konsep akar dan pangkat telah berkembang sejak zaman kuno. Bangsa Babilonia kuno (sekitar 2000 SM) sudah memiliki pengetahuan tentang akar kuadrat dan cara menghitungnya. Mereka menggunakan metode yang mirip dengan algoritma pembagian untuk menemukan akar kuadrat dari suatu bilangan.
Bangsa Yunani kuno, seperti Pythagoras, juga mempelajari akar kuadrat dan menemukan hubungan antara sisi-sisi segitiga siku-siku (Teorema Pythagoras), yang melibatkan penggunaan akar kuadrat.
Pada abad pertengahan, matematikawan India mengembangkan notasi pangkat yang lebih modern. Matematikawan Arab, seperti Al-Khwarizmi, berkontribusi pada pengembangan aljabar, termasuk metode untuk menyelesaikan persamaan kuadrat yang melibatkan akar kuadrat.
Perkembangan notasi pangkat modern dimulai pada abad ke-16 dengan René Descartes, yang memperkenalkan notasi x 2, x 3, dan seterusnya. Isaac Newton dan Gottfried Wilhelm Leibniz mengembangkan kalkulus, yang memberikan dasar yang lebih kuat untuk memahami konsep pangkat dan akar.
Tokoh-tokoh penting yang berkontribusi dalam pengembangan konsep ini:
- Bangsa Babilonia: Mengembangkan metode awal untuk menghitung akar kuadrat.
- Pythagoras: Menemukan hubungan antara sisi-sisi segitiga siku-siku yang melibatkan akar kuadrat.
- Al-Khwarizmi: Mengembangkan metode untuk menyelesaikan persamaan kuadrat.
- René Descartes: Memperkenalkan notasi pangkat modern.
- Isaac Newton dan Gottfried Wilhelm Leibniz: Mengembangkan kalkulus, yang memberikan landasan yang lebih kuat untuk memahami pangkat dan akar.
Penggunaan Akar dan Pangkat dalam Pemrograman Komputer
Akar dan pangkat digunakan secara luas dalam pemrograman komputer untuk berbagai aplikasi, mulai dari perhitungan matematika sederhana hingga simulasi kompleks. Bahasa pemrograman menyediakan fungsi bawaan (built-in functions) untuk menghitung akar kuadrat dan pangkat.
Contoh kode sederhana dalam bahasa pemrograman Python untuk menghitung akar kuadrat dan pangkat dua:
import math # Menghitung akar kuadrat angka = 25 akar_kuadrat = math.sqrt(angka) print(f"Akar kuadrat dari angka adalah akar_kuadrat") # Output: Akar kuadrat dari 25 adalah 5.0 # Menghitung pangkat dua basis = 3 pangkat = 2 hasil_pangkat = basis -* pangkat print(f"basis pangkat pangkat adalah hasil_pangkat") # Output: 3 pangkat 2 adalah 9
Penjelasan:
import math: Mengimpor modul math, yang berisi fungsi matematika seperti sqrt (akar kuadrat).math.sqrt(angka): Menghitung akar kuadrat dari variabel ‘angka’.basis pangkat: Menghitung basis dipangkatkan dengan pangkat menggunakan operator .
Dalam pemrograman, akar dan pangkat digunakan dalam berbagai aplikasi, seperti:
- Grafika komputer (transformasi geometris, penskalaan).
- Simulasi fisika (perhitungan gerak, gaya).
- Analisis data (pemrosesan sinyal, machine learning).
- Keuangan (perhitungan bunga majemuk, investasi).
Mengubah Akar Kuadrat Menjadi Pangkat
Mengubah akar kuadrat menjadi bentuk pangkat adalah keterampilan matematika fundamental yang membuka pintu ke pemahaman yang lebih dalam tentang aljabar dan konsep matematika lainnya. Kemampuan ini memungkinkan kita untuk menyederhanakan ekspresi, memecahkan persamaan, dan memahami hubungan antara berbagai jenis bilangan. Artikel ini akan membahas secara mendalam tentang bagaimana mengubah akar kuadrat menjadi pangkat, langkah-langkahnya, contoh soal, serta aplikasinya dalam berbagai konteks.
Mari kita mulai dengan memahami konsep dasarnya.
Pemahaman Konsep Dasar
Akar kuadrat dan pangkat adalah dua konsep matematika yang saling terkait erat. Memahami hubungan keduanya sangat penting untuk menguasai konversi akar kuadrat menjadi pangkat.
Akar kuadrat adalah operasi matematika yang mencari nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Simbol akar kuadrat adalah “√”. Misalnya, √9 = 3, karena 3 x 3 = 9.
Pangkat, di sisi lain, adalah cara untuk menyatakan perkalian berulang dari suatu bilangan. Bilangan yang dipangkatkan disebut basis, dan bilangan yang menunjukkan berapa kali basis dikalikan dengan dirinya sendiri disebut eksponen. Misalnya, 2 3 = 2 x 2 x 2 = 8. Di sini, 2 adalah basis dan 3 adalah eksponen.
Hubungan fundamental antara akar kuadrat dan pangkat pecahan adalah bahwa akar kuadrat dari suatu bilangan sama dengan bilangan tersebut dipangkatkan dengan 1/2. Dengan kata lain, √x = x (1/2).
Sebagai contoh, mari kita ilustrasikan √16 = 16 (1/2) =
4. Kita bisa membayangkan ini sebagai berikut: kita mencari bilangan yang jika dikalikan dengan dirinya sendiri menghasilkan 16. Bilangan itu adalah 4. Konsep ini diperluas ke akar pangkat lainnya. Misalnya, akar kubik dari x (∛x) sama dengan x dipangkatkan dengan 1/3 (x (1/3)).
Akar pangkat empat dari x ( 4√x) sama dengan x dipangkatkan dengan 1/4 (x (1/4)), dan seterusnya. Perhatikan bahwa indeks akar (angka kecil di atas simbol akar) menjadi penyebut dalam eksponen pecahan.
Sebagai contoh visual, kita bisa menggunakan grafik sederhana. Jika kita memplot fungsi y = x (1/2), kita akan melihat kurva yang dimulai dari titik (0,0) dan meningkat secara bertahap. Nilai y (hasil akar kuadrat) akan selalu lebih kecil dari nilai x (bilangan di bawah akar) untuk nilai x yang lebih besar dari 1.
Perbedaan utama antara akar kuadrat dan akar pangkat lainnya terletak pada indeks akar. Akar kuadrat memiliki indeks 2 (meskipun biasanya tidak ditulis), sedangkan akar kubik memiliki indeks 3, akar pangkat empat memiliki indeks 4, dan seterusnya. Konsep pangkat pecahan tetap sama: indeks akar menjadi penyebut dalam eksponen.
Langkah-Langkah Detail Konversi
Mengubah akar kuadrat menjadi bentuk pangkat pecahan melibatkan beberapa langkah sederhana. Berikut adalah langkah-langkah detailnya:
- Identifikasi basis: Tentukan bilangan di bawah simbol akar kuadrat. Ini adalah basis yang akan dipangkatkan.
- Tentukan eksponen: Eksponen untuk akar kuadrat selalu 1/2.
- Ubah akar kuadrat menjadi pangkat 1/2: Tuliskan basis dengan eksponen 1/2. Misalnya, √9 menjadi 9 (1/2).
- Sederhanakan jika memungkinkan: Jika basis dapat disederhanakan, lakukan penyederhanaan. Misalnya, 9 (1/2) = 3.
Mari kita lihat beberapa contoh rinci dengan berbagai jenis bilangan:
- Contoh 1: √9 = ?
Basisnya adalah 9. Eksponennya adalah 1/2. Oleh karena itu, √9 = 9 (1/2) = 3. - Contoh 2: √(16/25) = ?
Basisnya adalah 16/25. Eksponennya adalah 1/2. Oleh karena itu, √(16/25) = (16/25) (1/2) = 4/5. Kita bisa menyederhanakan lebih lanjut dengan mengambil akar kuadrat dari pembilang dan penyebut secara terpisah. - Contoh 3: √2.25 = ?
Basisnya adalah 2.25. Eksponennya adalah 1/2. Oleh karena itu, √2.25 = 2.25 (1/2) = 1.5.
Sekarang, mari kita bahas contoh dengan koefisien di depan akar kuadrat:
Misalnya, 2√4. Dalam hal ini, kita hanya mengubah akar kuadrat menjadi bentuk pangkat, sementara koefisien (2) tetap ada. Jadi, 2√4 = 2
– 4 (1/2) = 2
– 2 = 4.
Penanganan Variabel
Mengubah akar kuadrat dari variabel menjadi bentuk pangkat adalah konsep yang penting dalam aljabar. Aturannya tetap sama: akar kuadrat dari suatu variabel sama dengan variabel tersebut dipangkatkan dengan 1/2.
Berikut adalah beberapa contoh:
- √x: Ini sama dengan x (1/2).
- √(x2): Ini sama dengan (x 2) (1/2) = x (2
– 1/2) = x 1 = x. - √(x3): Ini sama dengan (x 3) (1/2) = x (3
– 1/2) = x (3/2).
Dalam contoh-contoh di atas, kita menggunakan aturan perkalian pangkat, yaitu (x a) b = x (a
– b) . Aturan eksponen lainnya yang relevan adalah aturan pembagian pangkat, yaitu x a / x b = x (a – b).
Sekarang, mari kita lihat contoh yang melibatkan kombinasi variabel dan konstanta: √(4x 2). Dalam hal ini, kita bisa mengambil akar kuadrat dari konstanta dan variabel secara terpisah. √(4x 2) = √4
– √(x 2) = 2
– x = 2x.
Contoh Soal dan Solusi
Berikut adalah tabel yang berisi contoh soal beserta solusi lengkapnya:
| Soal (Akar Kuadrat) | Solusi (Bentuk Pangkat) | Langkah-langkah Penyelesaian |
|---|---|---|
| √25 | 25(1/2) = 5 | Identifikasi basis (25). Ubah menjadi bentuk pangkat (25(1/2)). Sederhanakan (5). |
| √(49/64) | (49/64)(1/2) = 7/8 | Identifikasi basis (49/64). Ubah menjadi bentuk pangkat ((49/64)(1/2)). Sederhanakan (7/8). |
| √1.44 | 1.44(1/2) = 1.2 | Identifikasi basis (1.44). Ubah menjadi bentuk pangkat (1.44(1/2)). Sederhanakan (1.2). |
| 3√16 | 3
|
Identifikasi basis (16). Ubah menjadi bentuk pangkat (16(1/2)). Sederhanakan akar kuadrat (4). Kalikan dengan koefisien (3 – 4 = 12). |
| √(9x2) | √9
|
Identifikasi basis (9x2). Ambil akar kuadrat dari konstanta dan variabel secara terpisah. √9 = 3, √(x 2) = x. Hasilnya 3x. |
| √(x4y 6) | (x4) (1/2)
|
Identifikasi basis (x4y 6). Gunakan aturan perkalian pangkat. (x 4) (1/2) = x 2 dan (y 6) (1/2) = y 3. Hasilnya x 2y 3. |
Contoh soal yang melibatkan penyederhanaan ekspresi pangkat setelah konversi: (x (1/2)) 4 = x (1/2
– 4) = x 2.
Contoh soal yang melibatkan penggunaan sifat-sifat eksponen: x (3/2) / x (1/2) = x (3/2 – 1/2) = x 1 = x.
Soal Latihan
Berikut adalah soal latihan untuk menguji pemahaman Anda:
- Mudah:
- √16 = ?
- √81 = ?
- √100 = ?
- Sedang:
- √(25/36) = ?
- √0.09 = ?
- √(4x2) = ?
- Sulit:
- √(16x4y 6) = ?
- (x (1/2) – x 3) 2 = ?
- √(9(x – 2) 2) = ?
Kunci Jawaban:
- Mudah:
- 4
- 9
- 10
- Sedang:
- 5/6
- 0.3
- 2x
- Sulit:
- 4x2y 3
- x 7
- 3|x – 2|
Petunjuk (Hints) untuk soal sulit: Soal sulit seringkali melibatkan kombinasi konsep. Ingatlah untuk menggunakan aturan eksponen dan menyederhanakan ekspresi sebanyak mungkin. Untuk soal nomor 9, perhatikan nilai mutlak karena akar kuadrat dari kuadrat selalu positif.
Aplikasi dalam Konteks
Konversi akar kuadrat menjadi pangkat memiliki aplikasi praktis dalam berbagai bidang matematika dan ilmu pengetahuan.
Dalam aljabar, konsep ini digunakan untuk menyederhanakan ekspresi yang melibatkan akar kuadrat, memecahkan persamaan kuadrat, dan memanipulasi fungsi. Dalam kalkulus, konsep ini digunakan dalam turunan dan integral dari fungsi akar kuadrat.
Dalam bidang ilmu pengetahuan, konsep ini digunakan dalam berbagai aplikasi, seperti dalam fisika (misalnya, dalam perhitungan kecepatan dan percepatan), dalam rekayasa (misalnya, dalam perhitungan tegangan dan regangan), dan dalam keuangan (misalnya, dalam perhitungan pertumbuhan eksponensial). Sebagai contoh, dalam perhitungan jarak tempuh sebuah benda yang jatuh bebas, kita menggunakan rumus d = (1/2)gt 2, di mana d adalah jarak, g adalah percepatan gravitasi, dan t adalah waktu.
Untuk mencari waktu (t), kita perlu mengambil akar kuadrat dari ekspresi yang melibatkan d dan g. Ini menunjukkan bagaimana konversi akar kuadrat menjadi pangkat dapat digunakan untuk memecahkan masalah praktis.
Mengubah Akar Pangkat Tiga Menjadi Pangkat
Setelah memahami konversi akar kuadrat menjadi bentuk pangkat, kini saatnya kita menyelami lebih dalam konsep akar pangkat tiga. Perubahan ini melibatkan pemahaman tentang bagaimana nilai yang dikalikan tiga kali oleh dirinya sendiri menghasilkan suatu bilangan, dan bagaimana proses ini berelasi dengan representasi pangkat pecahan. Mari kita bedah lebih lanjut.
Perbedaan Konversi Akar Kuadrat dan Akar Pangkat Tiga
Perbedaan utama antara mengubah akar kuadrat dan akar pangkat tiga menjadi bentuk pangkat terletak pada eksponen atau pangkat yang digunakan. Sementara keduanya melibatkan representasi akar dalam bentuk pangkat pecahan, nilai pecahan yang digunakan berbeda. Berikut perbedaannya:
- Akar Kuadrat: Akar kuadrat dari suatu bilangan (misalnya, √x) dapat dituliskan sebagai x 1/2. Ini berarti kita mencari nilai yang, jika dikalikan oleh dirinya sendiri, akan menghasilkan x. Pangkat 1/2 mencerminkan bahwa kita mencari “setengah” dari pangkat yang dibutuhkan untuk menghasilkan bilangan tersebut.
- Akar Pangkat Tiga: Akar pangkat tiga dari suatu bilangan (misalnya, ∛x) dapat dituliskan sebagai x 1/3. Ini berarti kita mencari nilai yang, jika dikalikan oleh dirinya sendiri sebanyak tiga kali, akan menghasilkan x. Pangkat 1/3 mencerminkan bahwa kita mencari “sepertiga” dari pangkat yang dibutuhkan.
Perbedaan ini sangat penting karena menentukan bagaimana kita menginterpretasikan dan menghitung nilai akar tersebut. Memahami perbedaan ini krusial untuk menghindari kesalahan dalam perhitungan.
Contoh Soal Akar Pangkat Tiga ke Bentuk Pangkat Pecahan
Mari kita ambil contoh konkret untuk mengilustrasikan konversi akar pangkat tiga menjadi bentuk pangkat pecahan. Misalkan kita memiliki soal: ∛27. Kita akan mengubahnya menjadi bentuk pangkat.
- Identifikasi Bilangan: Bilangan yang akan kita cari akar pangkat tiganya adalah 27.
- Tulis dalam Bentuk Pangkat: ∛27 dapat ditulis sebagai 27 1/3.
- Faktorkan Bilangan: Cari bilangan yang jika dipangkatkan tiga menghasilkan 27. Kita tahu bahwa 3 x 3 x 3 = 27, atau 3 3 = 27.
- Substitusi: Gantikan 27 dengan 3 3 dalam persamaan: (3 3) 1/3.
- Sederhanakan: Gunakan sifat pangkat dari pangkat, yaitu (a m) n = a m*n. Maka, (3 3) 1/3 = 3 3*(1/3) = 3 1 = 3.
Jadi, ∛27 = 3.
Demonstrasi Mengubah Akar Pangkat Tiga Bilangan Negatif
Mengubah akar pangkat tiga dari bilangan negatif melibatkan konsep yang sama, tetapi dengan perhatian khusus pada tanda negatif. Berikut demonstrasi langkah demi langkah:
- Soal: ∛-8
- Tulis dalam Bentuk Pangkat: ∛-8 = (-8) 1/3
- Faktorkan Bilangan: Cari bilangan yang jika dikalikan tiga kali menghasilkan -8. Kita tahu bahwa -2 x -2 x -2 = -8, atau (-2) 3 = -8. Perhatikan bahwa tanda negatif tetap dipertahankan.
- Substitusi: Gantikan -8 dengan (-2) 3: ((-2) 3) 1/3
- Sederhanakan: Gunakan sifat pangkat dari pangkat: ((-2) 3) 1/3 = (-2) 3*(1/3) = (-2) 1 = -2.
Jadi, ∛-8 = -2. Penting untuk diingat bahwa akar pangkat tiga dari bilangan negatif akan selalu menghasilkan bilangan negatif.
Tips Mempermudah Konversi Akar Pangkat Tiga
Berikut adalah beberapa tips yang dapat mempermudah proses konversi akar pangkat tiga ke bentuk pangkat:
- Hafalkan Pangkat Tiga: Hafalkan pangkat tiga dari beberapa bilangan bulat kecil (1, 2, 3, 4, 5, dst.). Ini akan membantu Anda dengan cepat mengidentifikasi faktor dari bilangan yang diberikan. Contohnya: 1 3=1, 2 3=8, 3 3=27, 4 3=64, 5 3=125.
- Faktorkan dengan Cermat: Jika bilangan yang diberikan lebih besar atau sulit dikenali, lakukan faktorisasi prima. Ini akan membantu Anda menemukan faktor-faktor yang tepat.
- Perhatikan Tanda: Ingatlah bahwa akar pangkat tiga dari bilangan negatif akan selalu negatif. Pastikan untuk mempertahankan tanda negatif selama proses perhitungan.
- Gunakan Kalkulator (dengan Hati-hati): Kalkulator dapat membantu, tetapi pahami konsep dasarnya terlebih dahulu. Gunakan kalkulator untuk memverifikasi jawaban Anda, bukan sebagai pengganti pemahaman.
- Latihan Rutin: Semakin banyak Anda berlatih, semakin mudah Anda mengidentifikasi pola dan menyelesaikan soal dengan cepat dan akurat.
Mengubah Akar Pangkat n Menjadi Pangkat
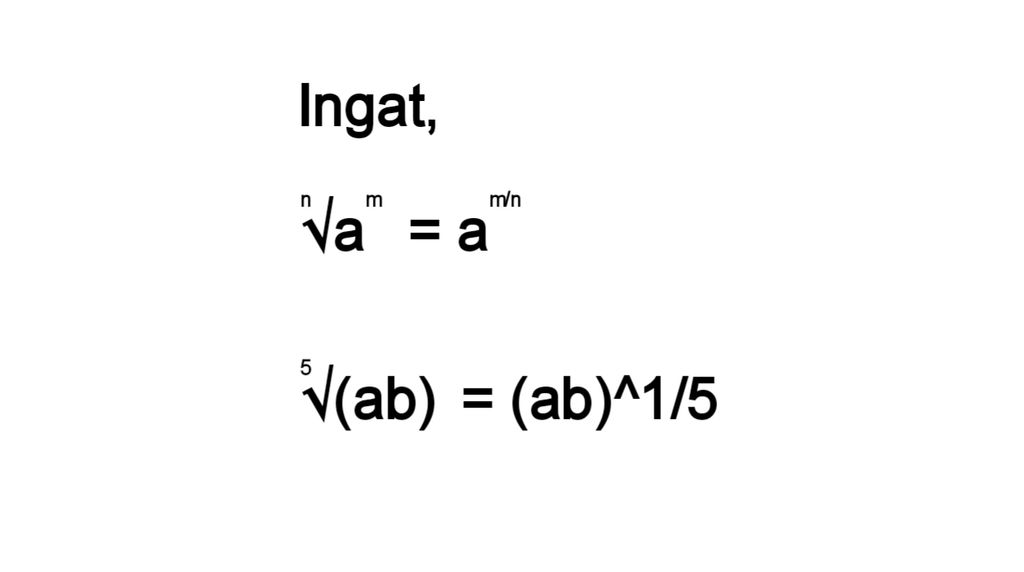
Source: ruangguru.com
Konversi akar pangkat n menjadi bentuk pangkat adalah keterampilan fundamental dalam matematika. Kemampuan ini memungkinkan penyederhanaan ekspresi aljabar, mempermudah penyelesaian persamaan, dan membuka pemahaman yang lebih dalam tentang hubungan antara berbagai konsep matematika. Dalam artikel ini, kita akan menjelajahi secara rinci bagaimana mengubah akar pangkat n menjadi bentuk pangkat, mulai dari aturan dasar hingga aplikasi praktis, disertai dengan contoh soal dan visualisasi yang komprehensif.
Aturan Dasar dan Prinsip Konversi
Konversi akar pangkat n menjadi bentuk pangkat didasarkan pada prinsip dasar eksponen dan akar. Secara sederhana, akar pangkat n dari suatu bilangan x dapat dinyatakan sebagai x yang dipangkatkan dengan pecahan 1/n. Prinsip ini berasal dari definisi akar itu sendiri, yang merupakan operasi kebalikan dari pemangkatan. Hubungan ini memungkinkan kita untuk mengubah bentuk akar yang rumit menjadi bentuk pangkat yang lebih mudah diolah.
Berikut adalah aturan dasar dan prinsip yang perlu dipahami:
- Indeks Akar (n): Menentukan jenis akar yang diambil. Misalnya, akar kuadrat memiliki indeks 2, akar pangkat tiga memiliki indeks 3, dan seterusnya.
- Basis (x): Bilangan yang akan diakarkan. Ini adalah nilai yang akan dihitung akarnya.
- Eksponen Pecahan: Bentuk pangkat yang dihasilkan dari konversi akar. Eksponen ini selalu berupa pecahan, dengan pembilang 1 dan penyebut sama dengan indeks akar.
Secara matematis, konversi ini dapat dirumuskan sebagai berikut:
√[n]x = x^(1/n)
Aturan Umum: Langkah-langkah Konversi
Untuk mengubah akar pangkat n menjadi bentuk pangkat, ikuti langkah-langkah berikut:
- Identifikasi Indeks Akar (n): Tentukan nilai n dari akar yang diberikan. Ini adalah angka kecil yang terletak di atas simbol akar (√). Jika tidak ada angka yang tertulis, berarti n = 2 (akar kuadrat).
- Identifikasi Basis (x): Tentukan bilangan yang berada di bawah simbol akar. Ini adalah nilai yang akan diakarkan.
- Tuliskan dalam Bentuk Pangkat: Tuliskan basis (x) yang dipangkatkan dengan pecahan 1/n.
- Sederhanakan (Jika Perlu): Jika memungkinkan, sederhanakan ekspresi pangkat tersebut.
Contoh: Ubah √[3]8 menjadi bentuk pangkat.
- Identifikasi Indeks Akar (n): n = 3
- Identifikasi Basis (x): x = 8
- Tuliskan dalam Bentuk Pangkat: 8^(1/3)
- Sederhanakan (Jika Perlu): 8^(1/3) = 2 (karena 2*2*2 = 8)
Contoh Soal dan Variasi Nilai n
Berikut adalah beberapa contoh soal yang melibatkan konversi akar pangkat n menjadi bentuk pangkat, dengan variasi nilai n dan kombinasi operasi matematika:
- Soal 1: Ubah √[4]16 menjadi bentuk pangkat.
- Identifikasi: n = 4, x = 16
- Konversi: 16^(1/4)
- Sederhanakan: 16^(1/4) = 2 (karena 2*2*2*2 = 16)
- Soal 2: Ubah √[3]27 – 2 menjadi bentuk pangkat dan selesaikan.
- Identifikasi: n = 3, x = 27
- Konversi: 27^(1/3)
- Sederhanakan: 27^(1/3) = 3
- Selesaikan: 3 – 2 = 1
- Soal 3: Ubah √[1/2]9 menjadi bentuk pangkat.
- Identifikasi: n = 1/2, x = 9
- Konversi: 9^(1/(1/2)) = 9^2
- Sederhanakan: 9^2 = 81
- Soal 4: Ubah √[-2]4 menjadi bentuk pangkat.
- Identifikasi: n = -2, x = 4
- Konversi: 4^(1/-2) = 4^(-1/2)
- Sederhanakan: 4^(-1/2) = 1 / 4^(1/2) = 1/2
- Soal 5: Hitung (√[3]8) – (√[2]9).
- Konversi akar pertama: √[3]8 = 8^(1/3) = 2
- Konversi akar kedua: √[2]9 = 9^(1/2) = 3
- Hitung: 2 – 3 = 6
Diagram Alir Visualisasi
Berikut adalah diagram alir yang memvisualisasikan proses konversi akar pangkat n menjadi bentuk pangkat:
Diagram alir dimulai dengan simbol “Mulai” (lingkaran). Kemudian, simbol “Proses” (persegi panjang) digunakan untuk mengidentifikasi nilai n dan x dari ekspresi akar. Selanjutnya, simbol “Proses” digunakan untuk mengubah bentuk akar menjadi bentuk pangkat, dengan eksponen pecahan 1/n. Setelah itu, simbol “Keputusan” (belah ketupat) digunakan untuk menentukan apakah ekspresi pangkat dapat disederhanakan. Jika ya, simbol “Proses” digunakan untuk menyederhanakan ekspresi.
Jika tidak, proses berlanjut langsung ke simbol “Selesai” (lingkaran). Contoh konkret ditampilkan di setiap langkah, seperti √[3]8 -> 8^(1/3) -> 2. Diagram alir ini mencakup semua kemungkinan skenario, termasuk penyederhanaan dan kasus di mana penyederhanaan tidak diperlukan.
Kasus Khusus dan Penanganannya
Beberapa kasus khusus perlu diperhatikan dalam konversi akar pangkat n menjadi bentuk pangkat:
- Akar Pangkat Nol (n = 0): Secara umum, akar pangkat nol tidak didefinisikan dalam matematika. Ekspresi seperti √[0]x tidak memiliki makna yang jelas.
- Akar Pangkat Negatif (n < 0): Akar pangkat negatif didefinisikan, tetapi menghasilkan eksponen pecahan negatif. Misalnya, √[-2]4 = 4^(-1/2). Eksponen negatif menunjukkan kebalikan dari basis yang dipangkatkan.
- Akar dari Bilangan Negatif: Akar dari bilangan negatif (√[n]-x) memiliki beberapa batasan.
- Jika n adalah bilangan genap, akar dari bilangan negatif tidak didefinisikan dalam bilangan real. Misalnya, √[-4]-16 tidak memiliki solusi real.
- Jika n adalah bilangan ganjil, akar dari bilangan negatif didefinisikan dan menghasilkan bilangan negatif. Misalnya, √[3]-8 = -2.
Contoh Soal Kasus Khusus:
- Soal 1 (Akar Pangkat Negatif): Ubah √[-3]-27 menjadi bentuk pangkat.
- Identifikasi: n = -3, x = -27
- Konversi: (-27)^(1/-3) = (-27)^(-1/3)
- Sederhanakan: (-27)^(-1/3) = 1 / (-27)^(1/3) = 1 / -3 = -1/3
- Soal 2 (Akar dari Bilangan Negatif, n ganjil): Ubah √[3]-64 menjadi bentuk pangkat.
- Identifikasi: n = 3, x = -64
- Konversi: (-64)^(1/3)
- Sederhanakan: (-64)^(1/3) = -4 (karena -4
– -4
– -4 = -64)
Tabel Ringkasan, Cara mengubah akar menjadi pangkat
Tabel berikut merangkum hubungan antara bentuk akar pangkat n dan bentuk pangkatnya:
| Bentuk Akar (√[n]x) | Bentuk Pangkat (x^(1/n)) | Keterangan | Contoh |
|---|---|---|---|
| √[2]9 | 9^(1/2) | Akar kuadrat, n = 2 | √[2]9 = 3 |
| √[3]8 | 8^(1/3) | Akar pangkat tiga, n = 3 | √[3]8 = 2 |
| √[4]16 | 16^(1/4) | Akar pangkat empat, n = 4 | √[4]16 = 2 |
| √[-2]4 | 4^(-1/2) | Akar pangkat negatif, n < 0 | √[-2]4 = 1/2 |
| √[3]-27 | (-27)^(1/3) | Akar dari bilangan negatif, n ganjil | √[3]-27 = -3 |
Penerapan dalam Persamaan Aljabar: Cara Mengubah Akar Menjadi Pangkat
Mengubah bentuk akar menjadi bentuk pangkat pecahan adalah teknik krusial dalam menyelesaikan persamaan aljabar. Pendekatan ini bukan hanya menyederhanakan ekspresi yang kompleks, tetapi juga membuka pintu menuju solusi yang lebih mudah dijangkau. Dengan memahami konsep dasar eksponen dan bagaimana aturan-aturannya berlaku, siswa dapat menguasai alat yang ampuh untuk memecahkan berbagai jenis persamaan, mulai dari yang sederhana hingga yang rumit.
Mari kita selami lebih dalam bagaimana transformasi ini bekerja dan bagaimana ia dapat menjadi kunci untuk membuka potensi penuh dalam menyelesaikan persamaan aljabar.
Penjelasan Konseptual
Transformasi akar menjadi pangkat pecahan didasarkan pada hubungan fundamental antara akar dan eksponen. Akar, seperti akar kuadrat (√) atau akar kubik (∛), pada dasarnya adalah operasi kebalikan dari pemangkatan. Sebagai contoh, akar kuadrat dari suatu bilangan adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan awal. Mengubah akar menjadi pangkat pecahan memungkinkan kita untuk merepresentasikan operasi ini menggunakan eksponen, yang memudahkan manipulasi aljabar.
Misalnya, √x dapat ditulis sebagai x 1/2, dan ∛x dapat ditulis sebagai x 1/3. Konsep ini memungkinkan kita menerapkan aturan eksponen yang sudah dikenal, seperti aturan perkalian (x a
– x b = x a+b), aturan pembagian (x a / x b = x a-b), dan aturan pemangkatan ( (x a) b = x a*b). Dengan menggunakan aturan-aturan ini, kita dapat menyederhanakan ekspresi, mengisolasi variabel, dan memecahkan persamaan dengan lebih efisien.
Keuntungan spesifik dari penggunaan pangkat pecahan dalam konteks persamaan aljabar sangat beragam:
- Memudahkan penyederhanaan ekspresi yang kompleks: Mengubah akar menjadi pangkat memungkinkan kita untuk menggabungkan dan menyederhanakan suku-suku yang melibatkan akar dengan lebih mudah.
- Membantu dalam isolasi variabel: Dengan mengubah akar menjadi pangkat, kita dapat memanipulasi persamaan untuk mengisolasi variabel yang dicari, mempermudah pencarian solusi.
- Memfasilitasi penggunaan aturan turunan: (Untuk tingkat pendidikan yang lebih tinggi) Dalam kalkulus, aturan turunan untuk eksponen dapat diterapkan pada bentuk pangkat pecahan, memungkinkan kita untuk menemukan turunan dari fungsi yang melibatkan akar.
Penerapan dalam Rumus Fisika
Konsep akar dan pangkat memiliki peran krusial dalam berbagai rumus fisika, memungkinkan kita untuk memodelkan dan memahami fenomena alam dengan lebih akurat. Kemampuan untuk mengubah akar menjadi pangkat seringkali mempermudah perhitungan, manipulasi aljabar, dan interpretasi hasil. Dalam dunia fisika, pemahaman ini membuka pintu menuju penyelesaian masalah yang kompleks dan aplikasi praktis yang luas.
Mari kita selami lebih dalam bagaimana konsep ini diterapkan dalam berbagai aspek fisika.
Rumus Fisika yang Menggunakan Akar dan Pangkat
Banyak rumus fisika yang memanfaatkan akar dan pangkat untuk menggambarkan hubungan antar variabel. Mengubah akar menjadi pangkat seringkali mempermudah manipulasi rumus dan penyelesaian masalah. Sebagai contoh, dalam mekanika, energi kinetik dan energi potensial gravitasi melibatkan pangkat dua, sementara kecepatan gelombang dan periode osilasi sering melibatkan akar kuadrat.
Berikut adalah beberapa contoh rumus fisika yang menggunakan akar dan pangkat, beserta deskripsi dan contoh penerapannya:
| Rumus | Deskripsi | Contoh |
|---|---|---|
| Kecepatan Gelombang (v)
|
Kecepatan gelombang transversal pada tali, di mana T adalah tegangan tali dan μ adalah massa jenis linier tali. Akar kuadrat digunakan untuk menghitung kecepatan berdasarkan parameter tali. | Sebuah tali dengan tegangan 100 N dan massa jenis linier 0.01 kg/m memiliki kecepatan gelombang:
|
| Periode Osilasi Pegas (T)
Memahami konversi akar menjadi pangkat adalah kunci dalam matematika, membuka pintu ke pemahaman yang lebih dalam tentang eksponen. Sama seperti kita perlu memahami aturan untuk menyederhanakan ekspresi matematika, ada juga aturan dalam mengelola platform digital. Sebagai contoh, pernahkah Anda bertanya-tanya bagaimana seorang admin grup WhatsApp bisa menghapus grup? Prosesnya ternyata cukup sederhana, mirip dengan menyederhanakan persamaan matematika, yang penjelasannya bisa ditemukan di cara admin menghapus grup whatsapp. Kembali ke matematika, kemampuan untuk mengubah akar menjadi pangkat akan sangat membantu dalam menyelesaikan berbagai soal. |
Periode osilasi sebuah pegas, di mana m adalah massa benda dan k adalah konstanta pegas. Akar kuadrat digunakan untuk menghitung periode berdasarkan massa dan konstanta pegas. | Sebuah pegas dengan konstanta 20 N/m dan massa 0.5 kg memiliki periode:
|
| Energi Kinetik (Ek)
|
Energi kinetik sebuah benda, di mana m adalah massa benda dan v adalah kecepatan benda. Kecepatan dikuadratkan untuk menghitung energi kinetik. | Sebuah benda bermassa 2 kg bergerak dengan kecepatan 5 m/s memiliki energi kinetik:
|
| Energi Potensial Gravitasi (Ep)
|
Energi potensial gravitasi sebuah benda, di mana m adalah massa benda, g adalah percepatan gravitasi, dan h adalah ketinggian benda. | Sebuah benda bermassa 1 kg berada pada ketinggian 10 m dari permukaan bumi (g = 9.8 m/s²) memiliki energi potensial gravitasi:
|
| Hukum Coulomb (F)
|
Gaya listrik antara dua muatan, di mana q₁ dan q₂ adalah besar muatan, r adalah jarak antara muatan, dan k adalah konstanta Coulomb. Jarak dikuadratkan dalam penyebut. | Dua muatan sebesar 1 μC dan 2 μC terpisah sejauh 0.1 m. Gaya Coulombnya adalah:
|
| Hukum Gravitasi Newton (F)
|
Gaya gravitasi antara dua massa, di mana m₁ dan m₂ adalah massa, r adalah jarak antara pusat massa, dan G adalah konstanta gravitasi. Jarak dikuadratkan dalam penyebut. | Dua benda bermassa 10 kg dan 20 kg terpisah sejauh 1 m. Gaya gravitasi antara keduanya adalah:
|
Contoh Soal Fisika dan Solusinya
Berikut adalah contoh soal fisika yang melibatkan akar dan pangkat, beserta solusinya:
Soal: Sebuah benda dijatuhkan dari ketinggian 20 meter. Berapa kecepatan benda saat menyentuh tanah? (Gunakan percepatan gravitasi g = 9.8 m/s²)
Solusi:
- Gunakan rumus energi potensial gravitasi (Ep) dan energi kinetik (Ek):
- Ep = mgh
- Ek = (1/2)mv²
- Saat benda jatuh, energi potensial berubah menjadi energi kinetik. Dengan mengabaikan gesekan udara, energi mekanik (Em) sistem konstan:
- Em = Ep + Ek
- Pada awal, Em = Ep (karena v = 0)
- Saat menyentuh tanah, Em = Ek (karena h = 0)
- Jadi, Ep awal = Ek akhir
- mgh = (1/2)mv²
- Massa (m) dapat dihilangkan dari kedua sisi persamaan:
- gh = (1/2)v²
- Isolasi v²:
- v² = 2gh
- Untuk mencari v, ambil akar kuadrat dari kedua sisi:
- v = √(2gh)
- Substitusi nilai:
- v = √(2
– 9.8 m/s²
– 20 m) - v = √(392 m²/s²)
- v ≈ 19.8 m/s
Kesimpulan: Kecepatan benda saat menyentuh tanah adalah sekitar 19.8 m/s.
Mengubah Akar dalam Rumus Fisika untuk Memecahkan Masalah
Kemampuan untuk mengubah akar menjadi pangkat seringkali sangat berguna dalam memecahkan masalah fisika. Sebagai contoh, dalam rumus periode osilasi pegas, kita dapat mengubah akar menjadi pangkat untuk mempermudah perhitungan turunan atau analisis perilaku sistem. Contoh lainnya adalah dalam persamaan gerak, di mana akar kuadrat digunakan untuk menghitung waktu tempuh atau jarak yang ditempuh. Manipulasi aljabar yang tepat memungkinkan kita untuk menyederhanakan persamaan dan mendapatkan solusi yang lebih mudah diinterpretasikan.
Berikut adalah contoh yang menunjukkan bagaimana mengubah akar dalam rumus fisika untuk memecahkan masalah:
Contoh: Sebuah benda bermassa 0.5 kg dihubungkan pada pegas dengan konstanta pegas 20 N/m. Hitung periode osilasi pegas.
- Rumus periode osilasi pegas:
- Ubah akar menjadi pangkat:
- Substitusi nilai:
- Sederhanakan:
- Hitung:
- Hasil akhir:
T = 2π√(m/k)
T = 2π(m/k)^(1/2)
T = 2π(0.5 kg / 20 N/m)^(1/2)
T = 2π(0.025 s²)^(1/2)
T ≈ 2π - 0.158 s
T ≈ 0.99 s
Dengan mengubah akar menjadi pangkat, perhitungan menjadi lebih mudah dikelola, dan kita dapat dengan cepat menemukan periode osilasi pegas.
Penerapan dalam Konsep Geometri
Geometri, sebagai studi tentang bentuk, ukuran, posisi relatif, dan sifat-sifat ruang, seringkali memanfaatkan akar dan pangkat untuk melakukan perhitungan yang akurat. Konsep-konsep ini menjadi krusial dalam menentukan luas, volume, dan dimensi objek geometris. Mari kita telusuri bagaimana akar dan pangkat bekerja secara sinergis dalam berbagai aspek geometri.
Penggunaan Akar dan Pangkat dalam Perhitungan Geometri
Akar dan pangkat memainkan peran penting dalam berbagai perhitungan geometri. Mereka digunakan untuk menghitung luas, volume, dan dimensi objek geometris.
- Luas: Pangkat sering digunakan untuk menghitung luas bangun datar. Misalnya, luas persegi dihitung dengan mengkuadratkan panjang sisinya (s 2), sementara luas lingkaran dihitung dengan menggunakan πr 2 (π dikalikan dengan jari-jari kuadrat). Akar kuadrat digunakan untuk mencari panjang sisi persegi jika luasnya diketahui.
- Volume: Pangkat digunakan untuk menghitung volume bangun ruang. Volume kubus dihitung dengan memangkatkan tiga panjang sisinya (s 3), dan volume bola dihitung menggunakan rumus (4/3)πr 3 (empat per tiga dikalikan π dikalikan jari-jari pangkat tiga). Akar pangkat tiga digunakan untuk mencari panjang sisi kubus jika volumenya diketahui.
- Dimensi: Akar dan pangkat juga digunakan untuk menentukan dimensi objek. Misalnya, dalam geometri analitik, jarak antara dua titik dalam ruang tiga dimensi dapat dihitung menggunakan akar kuadrat dari jumlah kuadrat selisih koordinat x, y, dan z.
Contoh Soal Geometri yang Melibatkan Akar dan Pangkat
Berikut adalah beberapa contoh soal yang mengilustrasikan penggunaan akar dan pangkat dalam geometri, beserta solusinya:
- Soal: Sebuah persegi memiliki luas 144 cm 2. Berapakah panjang sisi persegi tersebut?
- Solusi: Untuk menemukan panjang sisi, kita perlu mencari akar kuadrat dari luas. √144 = 12 cm. Jadi, panjang sisi persegi adalah 12 cm.
- Soal: Sebuah kubus memiliki volume 216 cm 3. Berapakah panjang rusuk kubus tersebut?
- Solusi: Untuk menemukan panjang rusuk, kita perlu mencari akar pangkat tiga dari volume. ∛216 = 6 cm. Jadi, panjang rusuk kubus adalah 6 cm.
- Soal: Sebuah lingkaran memiliki luas 78.5 cm 2 (gunakan π ≈ 3.14). Berapakah jari-jari lingkaran tersebut?
- Solusi: Luas lingkaran = πr 2. 78.5 = 3.14r 2. r 2 = 78.5 / 3.14 = 25. r = √25 = 5 cm. Jadi, jari-jari lingkaran adalah 5 cm.
Ilustrasi Visual Penggunaan Akar dan Pangkat dalam Menghitung Volume
Berikut adalah deskripsi visual mengenai penggunaan akar dan pangkat dalam menghitung volume berbagai bentuk geometris:
- Kubus: Bayangkan sebuah kubus dengan sisi 3 cm. Untuk menghitung volumenya, kita menghitung 3 3 = 27 cm 3. Visualisasikan kubus ini sebagai tumpukan balok satuan berukuran 1 cm x 1 cm x 1 cm. Terdapat 9 balok satuan di lapisan dasar, dan ada 3 lapisan, sehingga total ada 27 balok satuan.
- Balok: Balok dengan panjang 4 cm, lebar 3 cm, dan tinggi 2 cm. Volumenya adalah 4 x 3 x 2 = 24 cm 3. Visualisasikan balok sebagai tumpukan balok satuan. Terdapat 12 balok satuan di lapisan dasar (4 x 3), dan ada 2 lapisan, sehingga total ada 24 balok satuan.
- Bola: Bayangkan sebuah bola dengan jari-jari 3 cm. Untuk menghitung volumenya, kita menggunakan rumus (4/3)πr 3. Volume = (4/3)
– 3.14
– 3 3 ≈ 113.04 cm 3. Visualisasikan bola ini sebagai ruang yang ditempati, yang dapat diisi dengan sejumlah volume tertentu. - Kerucut: Kerucut dengan jari-jari alas 3 cm dan tinggi 5 cm. Volume kerucut = (1/3)πr 2h = (1/3)
– 3.14
– 3 2
– 5 ≈ 47.1 cm 3. Visualisasikan kerucut sebagai sebagian dari volume silinder dengan jari-jari dan tinggi yang sama.
Contoh Soal Geometri Menantang
Berikut adalah contoh soal yang menggabungkan konsep geometri, akar, dan pangkat:
- Soal: Sebuah tangki berbentuk silinder memiliki diameter 10 meter dan tinggi 14 meter. Tangki tersebut akan diisi dengan air. Berapa volume air yang dapat ditampung tangki tersebut? Kemudian, jika tangki tersebut hanya terisi setengahnya, berapa tinggi air di dalam tangki?
- Solusi:
- Langkah 1: Hitung jari-jari (r). Diameter = 10 m, jadi r = 5 m.
- Langkah 2: Hitung volume silinder. Volume = πr 2h = 3.14
– 5 2
– 14 = 1099 m 3. - Langkah 3: Jika tangki terisi setengahnya, volume air = 1099 / 2 = 549.5 m 3.
- Langkah 4: Hitung tinggi air. Volume = πr 2h. 549.5 = 3.14
– 5 2
– h. h = 549.5 / (3.14
– 25) ≈ 7 m. - Jawaban: Tangki dapat menampung 1099 m 3 air. Jika terisi setengahnya, tinggi air adalah sekitar 7 meter.
Sifat-Sifat Pangkat dan Akar yang Perlu Diketahui
Memahami sifat-sifat pangkat dan akar adalah kunci untuk menguasai manipulasi ekspresi matematika yang melibatkan keduanya. Sifat-sifat ini memungkinkan kita untuk menyederhanakan, mengubah, dan menyelesaikan persamaan dengan lebih efisien. Dengan memahami sifat-sifat ini, kita dapat menghindari kesalahan umum dan mengembangkan kemampuan berpikir matematis yang lebih kuat. Mari kita selami lebih dalam tentang sifat-sifat dasar yang perlu diketahui.
Berbicara tentang matematika, mengubah akar menjadi pangkat adalah fondasi penting. Tapi, pernahkah Anda terpikir, bagaimana dengan keamanan informasi digital kita? Sama pentingnya, bukan? Misalnya, ketika Anda ingin mengakses informasi tanpa filter, Anda mungkin perlu tahu bagaimana cara menonaktifkan pencarian aman yandex. Kembali ke akar dan pangkat, pemahaman yang kuat tentang konsep ini akan membantu Anda menyelesaikan berbagai masalah matematika dengan lebih mudah dan efisien, membuka pintu ke pemahaman yang lebih dalam.
Sifat-Sifat Dasar Pangkat dan Akar
Pangkat dan akar memiliki beberapa sifat dasar yang memungkinkan kita untuk memanipulasi ekspresi matematika dengan lebih mudah. Beberapa sifat yang paling penting meliputi sifat distributif, komutatif, dan asosiatif, meskipun penerapannya sedikit berbeda dibandingkan dengan operasi dasar seperti penjumlahan dan perkalian. Mari kita uraikan sifat-sifat ini dan bagaimana mereka diterapkan dalam konteks pangkat dan akar.
- Sifat Distributif: Sifat distributif berkaitan dengan bagaimana operasi perkalian “mendistribusikan” dirinya terhadap operasi penjumlahan atau pengurangan. Dalam konteks pangkat dan akar, sifat ini berlaku saat kita memiliki akar dari suatu perkalian atau pembagian.
Contoh: √(ab) = √a
– √b
Contoh di atas menunjukkan bahwa akar dari perkalian dua bilangan sama dengan perkalian akar-akar dari masing-masing bilangan. Ini sangat berguna untuk menyederhanakan ekspresi yang melibatkan akar.
- Sifat Komutatif: Sifat komutatif menyatakan bahwa urutan operasi tidak memengaruhi hasilnya. Dalam konteks pangkat, sifat komutatif berlaku untuk perkalian dan penjumlahan, tetapi tidak untuk pengurangan atau pembagian. Untuk akar, sifat komutatif tidak secara langsung berlaku dalam arti yang sama seperti pada penjumlahan dan perkalian, karena urutan operasi dalam akar ditentukan oleh struktur ekspresi itu sendiri.
Contoh: a + b = b + a (berlaku untuk penjumlahan)
Contoh di atas menunjukkan bahwa urutan penjumlahan tidak mengubah hasilnya. Namun, untuk akar, kita lebih fokus pada bagaimana kita bisa mengubah bentuk ekspresi agar lebih mudah dikerjakan, bukan mengubah urutan operasi.
- Sifat Asosiatif: Sifat asosiatif menyatakan bahwa pengelompokan operasi tidak memengaruhi hasilnya. Sama seperti sifat komutatif, sifat asosiatif berlaku untuk penjumlahan dan perkalian, tetapi tidak untuk pengurangan atau pembagian. Dalam konteks pangkat dan akar, sifat asosiatif membantu kita dalam mengelompokkan faktor-faktor untuk menyederhanakan ekspresi.
Contoh: (a + b) + c = a + (b + c) (berlaku untuk penjumlahan)
Contoh di atas menunjukkan bahwa bagaimana kita mengelompokkan bilangan saat menjumlahkan tidak mengubah hasilnya. Dalam konteks akar, kita menggunakan sifat asosiatif untuk mengelompokkan faktor-faktor di dalam akar untuk menyederhanakannya.
Daftar Sifat-Sifat Pangkat dan Akar Beserta Contohnya
Berikut adalah daftar sifat-sifat pangkat dan akar yang paling umum beserta contohnya. Memahami dan mengingat sifat-sifat ini akan sangat membantu dalam memecahkan soal-soal matematika yang melibatkan pangkat dan akar.
- Sifat Pangkat:
- a m
– a n = a m+n (Perkalian dengan basis yang sama) - a m / a n = a m-n (Pembagian dengan basis yang sama)
- (a m) n = a m*n (Pangkat dari pangkat)
- (a*b) n = a n
– b n (Pangkat dari perkalian) - (a/b) n = a n / b n (Pangkat dari pembagian)
- a 0 = 1 (Pangkat nol)
- Sifat Akar:
- √(a*b) = √a
– √b (Akar dari perkalian) - √(a/b) = √a / √b (Akar dari pembagian)
- n√a m = a m/n (Mengubah akar menjadi pangkat pecahan)
Mempermudah Manipulasi Ekspresi Matematika
Pemahaman yang mendalam tentang sifat-sifat pangkat dan akar mempermudah manipulasi ekspresi matematika. Sebagai contoh, dengan menggunakan sifat distributif, kita dapat memecah akar dari suatu perkalian menjadi perkalian akar-akar dari masing-masing faktor. Hal ini seringkali menyederhanakan ekspresi dan memungkinkan kita untuk menemukan solusi yang lebih mudah. Misalnya, jika kita memiliki √(16
– 9), kita dapat menyederhanakannya menjadi √16
– √9 = 4
– 3 = 12.
Tanpa pengetahuan tentang sifat distributif, kita mungkin harus menghitung 16
– 9 terlebih dahulu (144) dan kemudian mencari akar kuadratnya, yang juga menghasilkan 12, tetapi membutuhkan lebih banyak langkah.
Demikian pula, sifat-sifat pangkat, seperti aturan pangkat dari pangkat, memungkinkan kita untuk menyederhanakan ekspresi yang kompleks dengan cepat. Misalnya, (2 3) 2 dapat disederhanakan menjadi 2 3*2 = 2 6 = 64. Tanpa pemahaman tentang sifat ini, kita mungkin harus menghitung 2 3 terlebih dahulu (8) dan kemudian mengkuadratkannya, yang juga menghasilkan 64, tetapi lagi-lagi, membutuhkan lebih banyak langkah.
Akar Pangkat Pecahan
Selamat datang! Dalam artikel ini, kita akan menjelajahi dunia akar pangkat pecahan. Konsep ini mungkin terdengar sedikit rumit pada awalnya, tetapi sebenarnya sangat berguna dan sering muncul dalam berbagai bidang. Mari kita selami lebih dalam untuk memahami bagaimana cara kerjanya dan bagaimana kita dapat menerapkannya dalam kehidupan sehari-hari.
Akar Pangkat Pecahan: Penjelasan dan Cara Kerjanya
Akar pangkat pecahan adalah cara lain untuk mengekspresikan operasi matematika yang melibatkan akar dan pangkat. Secara sederhana, akar pangkat pecahan menggabungkan konsep akar dan pangkat dalam satu notasi. Bentuk umumnya adalah am/n, di mana ‘a’ adalah basis, ‘m’ adalah pangkat, dan ‘n’ adalah indeks akar. Ini setara dengan mengambil akar ke-n dari a yang dipangkatkan m, atau n√a m.
Pemahaman ini sangat penting karena memungkinkan kita untuk menyederhanakan ekspresi yang kompleks dan memecahkan masalah yang melibatkan akar dan pangkat dengan lebih efisien.
Contoh Soal Akar Pangkat Pecahan
Mari kita lihat beberapa contoh soal untuk memperjelas konsep ini:
- Contoh 1: Sederhanakan 82/3.
- Kita bisa menganggap ini sebagai akar pangkat tiga dari 8 yang dikuadratkan, atau 3√8 2.
- 8 2 = 64.
- 3√64 = 4. Jadi, 82/3 = 4 .
- Contoh 2: Hitung 271/3.
- Ini berarti akar pangkat tiga dari 27, atau 3√27 .
- 3√27 = 3. Jadi, 271/3 = 3 .
- Contoh 3: Sederhanakan 163/4.
- Ini sama dengan akar pangkat empat dari 16 yang dipangkatkan tiga, atau 4√16 3.
- 16 3 = 4096.
- 4√4096 = 8. Jadi, 163/4 = 8 .
Ilustrasi Visual Akar Pangkat Pecahan
Untuk memvisualisasikan bagaimana akar pangkat pecahan berinteraksi, bayangkan sebuah garis bilangan.
Misalnya, untuk 91/2 (akar kuadrat dari 9), kita mencari nilai yang, jika dikalikan dengan dirinya sendiri, menghasilkan 9. Ini adalah 3. Pada garis bilangan, kita bisa melihat bahwa 3 adalah titik di mana akar kuadrat dari 9 berada.
Mungkin terdengar rumit, tapi mengubah akar menjadi pangkat sebenarnya serupa dengan membalik sebuah operasi matematika. Sama seperti kita bisa melacak lokasi iPhone menggunakan iCloud, pemahaman konsep akar dan pangkat membuka wawasan baru dalam perhitungan. Bayangkan, bagaimana kita bisa menguasai lebih banyak aspek matematika? Nah, dengan pemahaman yang baik tentang cara mengubah akar menjadi pangkat, kita bisa menyederhanakan banyak soal, sama seperti kemudahan yang kita dapatkan saat menggunakan cara melacak iphone dengan icloud untuk menemukan perangkat yang hilang.
Kembali lagi, menguasai konversi akar ke pangkat adalah kunci!
Sekarang, pertimbangkan 82/3. Kita bisa memvisualisasikannya dengan membayangkan sebuah kubus dengan volume 8. Untuk menemukan 81/3, kita mencari panjang sisi kubus tersebut, yang adalah 2. Kemudian, kita mengkuadratkan nilai ini (2 2), yang menghasilkan 4. Ini menunjukkan bagaimana akar pangkat pecahan menggabungkan operasi akar dan pangkat, yang dapat divisualisasikan secara geometris atau dengan menggunakan garis bilangan.
Penggunaan Akar Pangkat Pecahan dalam Konteks Dunia Nyata
Akar pangkat pecahan memiliki banyak aplikasi di dunia nyata:
- Bidang Teknik: Dalam rekayasa listrik, akar pangkat pecahan digunakan untuk menghitung impedansi dalam rangkaian AC. Impedansi adalah ukuran seberapa besar rangkaian menentang aliran arus.
- Bidang Keuangan: Dalam keuangan, akar pangkat pecahan digunakan dalam perhitungan nilai sekarang (present value) dan nilai masa depan (future value) dari investasi. Ini membantu dalam menghitung bunga majemuk dan menganalisis pengembalian investasi.
- Bidang Fisika: Dalam fisika, akar pangkat pecahan digunakan dalam berbagai rumus, misalnya dalam perhitungan kecepatan gelombang, periode osilasi, dan dalam mekanika kuantum.
- Bidang Komputer Grafik: Dalam pembuatan model 3D dan rendering, akar pangkat pecahan digunakan untuk menghitung posisi dan orientasi objek dalam ruang 3D, serta untuk mensimulasikan efek pencahayaan dan bayangan.
- Bidang Musik: Dalam musik, akar pangkat pecahan digunakan untuk menghitung frekuensi nada dalam sistem temperamen yang berbeda, seperti sistem temperamen rata-rata 12 nada.
Memecahkan Soal Kompleks
Kemampuan untuk mengubah akar menjadi pangkat menjadi sangat penting ketika berhadapan dengan soal matematika yang kompleks. Soal-soal ini seringkali melibatkan kombinasi akar, pangkat, dan operasi matematika lainnya, yang membutuhkan strategi penyelesaian yang terencana dan pemahaman yang mendalam. Artikel ini akan membahas bagaimana merancang strategi yang efektif dan memberikan contoh konkret untuk membantu Anda menguasai keterampilan ini.
Rancang Strategi untuk Memecahkan Soal yang Melibatkan Kombinasi Akar, Pangkat, dan Operasi Matematika Lainnya
Memecahkan soal kompleks yang melibatkan akar dan pangkat membutuhkan pendekatan sistematis. Berikut adalah beberapa langkah yang bisa diikuti:
- Identifikasi Masalah: Pahami dengan jelas apa yang diminta oleh soal. Identifikasi semua akar, pangkat, dan operasi matematika yang terlibat.
- Ubah Akar Menjadi Pangkat: Ubah semua akar menjadi bentuk pangkat untuk mempermudah perhitungan. Gunakan aturan √[n]a = a^(1/n).
- Sederhanakan Ekspresi: Gunakan sifat-sifat pangkat untuk menyederhanakan ekspresi. Ingat aturan seperti a^m
a^n = a^(m+n), (a^m)^n = a^(m*n), dan a^m / a^n = a^(m-n).
- Lakukan Operasi Matematika: Lakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian sesuai urutan yang benar (biasanya mengikuti aturan BODMAS/PEMDAS).
- Periksa Kembali: Setelah selesai, periksa kembali pekerjaan Anda untuk memastikan tidak ada kesalahan perhitungan.
Contoh Soal Kompleks Beserta Langkah-Langkah Penyelesaiannya
Mari kita ambil contoh soal berikut:
Sederhanakan: √(9x^4)
– (27x^6)^(1/3) / x^2
- Ubah Akar Menjadi Pangkat: √(9x^4) = (9x^4)^(1/2)
- Sederhanakan Ekspresi Pertama: (9x^4)^(1/2) = 9^(1/2)
x^(4*(1/2)) = 3x^2
- Sederhanakan Ekspresi Kedua: (27x^6)^(1/3) = 27^(1/3)
x^(6*(1/3)) = 3x^2
- Substitusi dan Sederhanakan: 3x^2
3x^2 / x^2 = 9x^4 / x^2 = 9x^2
- Hasil Akhir: 9x^2
Rangkuman Langkah-Langkah Kunci dalam Memecahkan Soal Kompleks yang Melibatkan Akar dan Pangkat
Langkah-langkah Kunci:
- Identifikasi: Kenali semua akar, pangkat, dan operasi.
- Konversi: Ubah akar menjadi bentuk pangkat.
- Sederhanakan: Gunakan sifat-sifat pangkat untuk menyederhanakan.
- Hitung: Lakukan operasi matematika sesuai urutan.
- Verifikasi: Periksa kembali jawaban Anda.
Soal Latihan Tingkat Lanjut yang Menguji Pemahaman tentang Mengubah Akar Menjadi Pangkat
Berikut adalah beberapa soal latihan untuk menguji pemahaman Anda:
- Sederhanakan: √[3](8x^6) / (4x^2)^(1/2)
- Sederhanakan: (16x^8)^(1/4)
√(25x^2) / (2x)
- Selesaikan untuk x: √(x+1) = 3
- Selesaikan untuk x: (x-2)^(1/2) = 4
- Sederhanakan: √(x^2 + 6x + 9)
Peran Eksponen Negatif
Eksponen negatif adalah konsep penting dalam matematika yang seringkali membingungkan bagi siswa. Memahami eksponen negatif memungkinkan kita untuk menyederhanakan ekspresi aljabar, menyelesaikan persamaan, dan memahami berbagai fenomena di dunia nyata. Artikel ini akan membahas secara mendalam tentang definisi, hubungan, contoh soal, ilustrasi visual, tips, dan trik terkait eksponen negatif.
Mari kita selami lebih dalam untuk memahami peran krusial eksponen negatif dalam matematika.
Definisi dan Konsep Dasar
Eksponen negatif, secara sederhana, menunjukkan kebalikan (reciprocal) dari suatu bilangan berpangkat positif. Dalam matematika, eksponen negatif mengindikasikan bahwa bilangan pokok (basis) dibagi, bukan dikalikan, berulang kali. Ini adalah konsep yang sangat penting untuk dipahami karena sering muncul dalam berbagai bidang matematika dan sains.
- Definisi Eksponen Negatif: Eksponen negatif didefinisikan sebagai
a-n = 1 / a n, dimana a ≠ 0.
Ini berarti bahwa a -n sama dengan 1 dibagi dengan a n.
- Interpretasi Kebalikan (Reciprocal): Eksponen negatif menunjukkan kebalikan dari bilangan pokok yang dipangkatkan. Contohnya, 2 -3 adalah kebalikan dari 2 3, yang berarti 1/8.
- Pembagian Berulang: Eksponen negatif merepresentasikan operasi pembagian berulang. Misalnya, 10 -2 sama dengan 1 dibagi dengan 10 dua kali (1 / 10 / 10), yang menghasilkan 0.01.
- Contoh Konkret:
- 2 -1 = 1/2 = 0.5
- 3 -2 = 1/3 2 = 1/9 ≈ 0.111
- 5 -3 = 1/5 3 = 1/125 = 0.008
- Perbandingan dengan Eksponen Positif: Eksponen positif menunjukkan perkalian berulang. Perbedaan mendasar terletak pada operasi yang dilakukan: perkalian (positif) vs. pembagian (negatif).
- 2 3 = 2
– 2
– 2 = 8 (perkalian berulang) - 2 -3 = 1 / (2
– 2
– 2) = 1/8 (pembagian berulang)
- 2 3 = 2
- Analogi untuk Siswa Sekolah Dasar: Bayangkan sebuah kue. Jika Anda membagi kue menjadi dua bagian yang sama, Anda memiliki 1/2 kue. Jika Anda membagi kue lagi menjadi dua bagian, Anda memiliki 1/4 kue (1/2 dari 1/2). Eksponen negatif membantu kita memahami bagaimana ukuran bagian kue tersebut berubah ketika kita membagi kue lebih banyak lagi.
Hubungan dengan Akar dan Pangkat
Eksponen negatif memiliki hubungan erat dengan akar dan pangkat positif. Memahami hubungan ini sangat penting untuk menyederhanakan ekspresi matematika dan menyelesaikan masalah yang lebih kompleks.
- Tabel Perbandingan:
| Eksponen Negatif | Akar | Pangkat Positif | Contoh Numerik |
|---|---|---|---|
| a-n | Tidak langsung, tetapi terkait melalui kebalikan | an | 2-2 = 1/4, √16 = 4, 22 = 4 |
| x-1 | Tidak langsung | x1 | 3-1 = 1/3, 31 = 3 |
| (am)-n | Terkait melalui akar pangkat n dari am | (am)n | (22)-1 = 1/4, (22)1 = 4 |
- Menyederhanakan Ekspresi yang Melibatkan Akar: Eksponen negatif dapat digunakan untuk menyederhanakan ekspresi yang melibatkan akar dengan mengubah akar menjadi bentuk pangkat.
- Mengubah Akar Menjadi Pangkat Negatif: Akar dapat diubah menjadi pangkat negatif dengan menggunakan aturan berikut:
- n√a m = a m/n
- Contoh: 3√8 = 8 1/3. Jika kita ingin mengubahnya menjadi bentuk negatif, kita bisa menulisnya sebagai 1 / (8 -1/3)
- Domain dan Range Fungsi: Eksponen negatif dapat mempengaruhi domain dan range fungsi eksponensial dan fungsi akar.
- Fungsi Eksponensial: Fungsi y = a -x (a > 0) memiliki domain semua bilangan real dan range (0, ∞). Grafiknya mendekati sumbu x (y = 0) tetapi tidak pernah menyentuhnya.
- Fungsi Akar: Fungsi akar yang melibatkan eksponen negatif, seperti y = √x -1, domainnya akan dibatasi karena kita tidak bisa mengambil akar dari bilangan negatif.
Contoh Soal dan Penyelesaian
Berikut adalah beberapa contoh soal yang melibatkan eksponen negatif, beserta solusi langkah demi langkah:
- Soal 1: Penyederhanaan Ekspresi
- Sederhanakan: 3x -2y 3 / (2x -1y)
- Solusi:
- Gunakan sifat eksponen untuk membagi variabel yang sama: x-2 / x -1 = x (-2 – (-1)) = x -1
- y 3 / y = y (3 – 1) = y 2
- Tulis ulang ekspresi: (3/2)
– x -1
– y 2 - Ubah x -1 menjadi 1/x: (3y 2) / (2x)
- Soal 2: Persamaan dengan Eksponen Negatif
- Selesaikan: 2 x = 1/8
- Solusi:
- Ubah 1/8 menjadi bentuk pangkat dengan basis 2: 1/8 = 2-3
- Persamaan menjadi: 2 x = 2 -3
- Karena basisnya sama, samakan eksponennya: x = -3
- Soal 3: Soal Cerita (Peluruhan Radioaktif)
- Suatu zat radioaktif meluruh dengan persamaan A(t) = A 0
– 2 -t/h, di mana A(t) adalah jumlah zat setelah waktu t, A 0 adalah jumlah awal zat, dan h adalah waktu paruh. Jika waktu paruh suatu zat adalah 10 tahun, berapa banyak zat yang tersisa setelah 20 tahun jika awalnya ada 100 gram? - Solusi:
- Gunakan persamaan: A(t) = A0
– 2 -t/h - Substitusikan nilai: A(20) = 100
– 2 -20/10 - Sederhanakan: A(20) = 100
– 2 -2 - Hitung: A(20) = 100
– (1/4) = 25 gram
- Gunakan persamaan: A(t) = A0
- Suatu zat radioaktif meluruh dengan persamaan A(t) = A 0
- Soal 4: Penyederhanaan Ekspresi (Lebih Kompleks)
- Sederhanakan: (4x -3y 2) -2
- Solusi:
- Terapkan aturan pangkat ke pangkat: 4-2
– x (-3
– -2)
– y (2
– -2) - Sederhanakan: 1/16
– x 6
– y -4 - Tulis ulang dengan eksponen positif: x 6 / (16y 4)
- Terapkan aturan pangkat ke pangkat: 4-2
- Soal 5: Persamaan dengan Beberapa Eksponen Negatif
- Selesaikan: (1/2) x = 8
- Solusi:
- Ubah basis menjadi sama: (2-1) x = 2 3
- Sederhanakan: 2 -x = 2 3
- Samakan eksponen: -x = 3
- Selesaikan untuk x: x = -3
- Kesalahan Umum: Kesalahan umum adalah lupa membalikkan basis saat mengubah eksponen negatif menjadi positif. Contohnya, siswa mungkin salah mengartikan 2 -2 sebagai -4, bukan 1/4.
Ilustrasi Visual
Berikut adalah beberapa ilustrasi visual untuk membantu memahami konsep eksponen negatif:
1. Grafik Fungsi: Grafik fungsi y = 2 -x adalah cerminan dari grafik y = 2 x terhadap sumbu y. Grafik y = 2 -x mendekati sumbu x (y = 0) saat x menjadi sangat besar (positif), tetapi tidak pernah menyentuhnya. Sebaliknya, grafik ini meningkat tajam saat x mendekati minus tak hingga.
2. Diagram Alir: Diagram alir akan menunjukkan langkah-langkah untuk mengubah ekspresi dengan eksponen negatif menjadi bentuk positif.Mari kita mulai dengan matematika, mengubah akar menjadi pangkat itu soal mudah, kan? Tapi, bagaimana kalau kita terapkan ke dunia kerja? Sama seperti mengubah akar, mencari pekerjaan baru juga butuh strategi. Pernahkah terpikir untuk langsung menanyakan lowongan kerja? Jangan ragu, karena cara menanyakan lowongan kerja secara langsung bisa jadi kunci.
Kembali ke matematika, setelah menguasai akar dan pangkat, dunia kerja juga akan terasa lebih mudah dihadapi.
- Mulai dengan ekspresi a -n.
- Ubah menjadi 1 / a n.
- Sederhanakan jika memungkinkan.
- Untuk mengubah akar menjadi pangkat negatif: n√a m -> a m/n, kemudian ubah menjadi 1/a -m/n.
-
3. Representasi Visual
Bayangkan sebuah persegi panjang dengan luas 1 unit. Jika kita membagi panjangnya menjadi dua, kita mendapatkan 1/2. Jika kita membagi lagi, kita mendapatkan 1/4. Ilustrasi ini dapat menunjukkan bagaimana eksponen negatif (misalnya, 2 -3 = 1/8) berkaitan dengan pembagian berulang dan bagaimana luasnya menjadi lebih kecil seiring dengan peningkatan eksponen negatif.
Tips dan Trik
Berikut adalah beberapa tips dan trik untuk mempermudah perhitungan yang melibatkan eksponen negatif:
1. Menggunakan Sifat-Sifat Eksponen: Manfaatkan sifat-sifat eksponen seperti a m
– a n = a m+n, a m / a n = a m-n, dan (a m) n = a m*n.
2. Mengubah Eksponen Negatif Menjadi Positif: Ubah eksponen negatif menjadi positif sesegera mungkin untuk menghindari kesalahan.
3. Memahami Urutan Operasi: Selalu ikuti urutan operasi (PEMDAS/BODMAS) saat mengerjakan soal yang melibatkan eksponen negatif.
4. Menggunakan Kalkulator: Gunakan kalkulator dengan benar untuk menghitung eksponen negatif, terutama untuk angka yang kompleks. Pastikan untuk memasukkan tanda kurung dengan benar.
5. Mengenali Pola: Perhatikan pola-pola umum dalam soal eksponen negatif. Ini akan membantu Anda memperkirakan jawaban dan memeriksa apakah perhitungan Anda benar.- Kesalahan Umum yang Harus Dihindari:
- Lupa membalikkan basis saat mengubah eksponen negatif.
- Kesalahan dalam menerapkan urutan operasi.
- Kesalahan dalam menghitung eksponen, terutama dengan angka pecahan.
- Contoh Soal yang Membutuhkan Logaritma: Selesaikan: 2 x = Untuk menyelesaikan soal ini, Anda perlu menggunakan logaritma: x = log 2(5). Logaritma adalah operasi kebalikan dari eksponensial, yang memungkinkan kita untuk menyelesaikan persamaan di mana variabel berada di eksponen.
Aplikasi di Bidang Teknologi
Konsep akar dan pangkat, yang mungkin terlihat sebagai bagian dasar dari matematika, ternyata memiliki peran yang sangat krusial dalam dunia teknologi modern. Dari algoritma kompleks hingga visualisasi grafis yang memukau, akar dan pangkat menjadi fondasi dari banyak aplikasi yang kita gunakan sehari-hari. Artikel ini akan membahas secara mendalam bagaimana konsep-konsep ini diterapkan dalam berbagai bidang teknologi, memberikan contoh konkret, ilustrasi visual, dan studi kasus untuk memberikan pemahaman yang komprehensif.
Oke, mari kita mulai dengan akar pangkat. Ingat, mengubah akar menjadi pangkat itu esensial dalam banyak perhitungan, bukan? Nah, bayangkan Anda sedang menyusun laporan keuangan di Excel. Untuk analisis yang lebih mendalam, Anda mungkin perlu melakukan perhitungan yang melibatkan akar kuadrat atau akar pangkat lainnya. Rumus-rumus ini sangat krusial, sama seperti memahami cara bikin laporan keuangan di excel.
Kembali ke akar pangkat, kemampuan untuk mengutak-atik angka dengan cara ini membuka pintu bagi analisis yang lebih kompleks dan akurat.
Pemahaman tentang akar dan pangkat tidak hanya penting bagi para matematikawan, tetapi juga bagi programmer, ilmuwan data, insinyur, dan siapa saja yang tertarik untuk memahami cara kerja teknologi di balik layar. Artikel ini akan mengungkap bagaimana konsep-konsep ini menjadi tulang punggung dari inovasi teknologi.
Penjelasan Konsep
Akar kuadrat, akar pangkat tiga, dan pangkat (eksponen) adalah konsep matematika yang digunakan untuk memecahkan berbagai masalah dalam teknologi. Mari kita telaah bagaimana konsep-konsep ini diterapkan dalam berbagai bidang:
- Pemrograman Komputer: Bahasa pemrograman seperti Python, C++, dan Java menggunakan akar dan pangkat untuk berbagai operasi matematika. Contohnya, menghitung jarak antara dua titik dalam ruang 2D atau 3D memerlukan penggunaan akar kuadrat. Operasi eksponensial digunakan dalam banyak algoritma, termasuk pemrosesan sinyal dan simulasi fisika.
- Analisis Data: Dalam statistik dan machine learning, akar dan pangkat digunakan dalam berbagai perhitungan. Misalnya, dalam analisis regresi, akar kuadrat digunakan untuk menghitung root mean squared error (RMSE), yang mengukur perbedaan antara nilai yang diprediksi dan nilai sebenarnya. Fungsi eksponensial digunakan dalam regresi logistik dan jaringan saraf tiruan.
- Grafika Komputer: Rendering 3D dan animasi sangat bergantung pada akar dan pangkat. Perhitungan pencahayaan, transformasi geometri, dan normalisasi vektor seringkali melibatkan operasi akar dan pangkat. Misalnya, untuk menghitung jarak antara kamera dan objek dalam adegan 3D, akar kuadrat digunakan.
- Pengolahan Sinyal: Dalam pengolahan audio dan gambar, akar dan pangkat digunakan untuk berbagai tugas. Misalnya, dalam pengolahan gambar, akar kuadrat digunakan untuk normalisasi piksel, sedangkan operasi eksponensial digunakan dalam transformasi Fourier.
- Kriptografi: Kriptografi modern, seperti enkripsi RSA, sangat bergantung pada operasi modular eksponensial. Keamanan data yang kita gunakan setiap hari bergantung pada kemampuan untuk melakukan perhitungan eksponensial yang kompleks dan efisien.
- Simulasi Fisika: Dalam pengembangan game dan rekayasa, akar dan pangkat digunakan untuk mensimulasikan perilaku dunia nyata. Misalnya, menghitung lintasan proyektil, simulasi gerakan objek, dan perhitungan gaya gravitasi semuanya melibatkan operasi akar dan pangkat.
Sebagai contoh analogi dunia nyata, bayangkan menghitung luas sebuah persegi panjang. Luas dihitung dengan mengalikan panjang dan lebar (pangkat). Jika kita ingin mencari panjang sisi persegi yang memiliki luas tertentu, kita menggunakan akar kuadrat. Dalam dunia teknologi, konsep ini diperluas ke dimensi yang lebih tinggi dan masalah yang lebih kompleks.
Contoh Konkret dan Implementasi
Mari kita lihat beberapa contoh konkret bagaimana akar dan pangkat digunakan dalam algoritma dan model matematika:
- Algoritma Jarak Euclidean: Dalam analisis data, jarak Euclidean digunakan untuk mengukur jarak antara dua titik dalam ruang multidimensi. Rumus untuk menghitung jarak Euclidean adalah:
d(p, q) = √((q₁
- p₁)² + (q₂
- p₂)² + … + (qₙ
- pₙ)²)
di mana p dan q adalah titik, dan n adalah jumlah dimensi. Algoritma ini memiliki kompleksitas waktu O(n) karena kita harus melakukan operasi pengurangan, pengkuadratan, penjumlahan, dan akar kuadrat untuk setiap dimensi. Kompleksitas ruang adalah O(1) karena kita hanya memerlukan ruang konstan untuk menyimpan hasil.
- Normalisasi Piksel dalam Pemrosesan Gambar: Dalam pemrosesan gambar, normalisasi piksel seringkali diperlukan untuk meningkatkan kualitas gambar. Salah satu metode normalisasi melibatkan penggunaan akar kuadrat. Misalnya, untuk normalisasi intensitas piksel, kita dapat menggunakan rumus:
I’ = √(I)
di mana I adalah intensitas piksel asli dan I’ adalah intensitas piksel yang dinormalisasi. Algoritma ini memiliki kompleksitas waktu O(n) di mana n adalah jumlah piksel dalam gambar. Kompleksitas ruang adalah O(1) karena kita hanya mengubah nilai piksel di tempat.
- Model Pertumbuhan Eksponensial: Dalam simulasi pertumbuhan populasi atau peluruhan radioaktif, fungsi eksponensial digunakan untuk memodelkan perubahan. Rumus untuk model pertumbuhan eksponensial adalah:
P(t) = P₀
e^(kt)
di mana P(t) adalah populasi pada waktu t, P₀ adalah populasi awal, e adalah bilangan Euler (sekitar 2.71828), dan k adalah laju pertumbuhan. Algoritma ini memiliki kompleksitas waktu O(1) untuk satu perhitungan, tetapi kompleksitas waktu dapat meningkat jika kita perlu menghitung pertumbuhan selama periode waktu yang panjang. Kompleksitas ruang adalah O(1).
Ilustrasi Visual Kode
Berikut adalah beberapa contoh kode Python yang mengilustrasikan penggunaan akar dan pangkat:
Contoh 1: Menghitung Jarak Euclidean
Kode Python di bawah ini menghitung jarak Euclidean antara dua titik dalam ruang 2D. Kode ini menerima dua tuple sebagai input, masing-masing mewakili koordinat titik. Kode menghitung perbedaan koordinat, mengkuadratkannya, menjumlahkannya, dan mengambil akar kuadrat dari hasilnya.
import math
def euclidean_distance(point1, point2):
"""
Menghitung jarak Euclidean antara dua titik.
"""
distance = math.sqrt(sum([(a - b)
-* 2 for a, b in zip(point1, point2)]))
return distance
# Contoh input:
point_a = (1, 2)
point_b = (4, 6)
# Output:
print(euclidean_distance(point_a, point_b)) # Output: 5.0
Contoh 2: Normalisasi Piksel
Kode Python ini mengilustrasikan normalisasi piksel dengan mengambil akar kuadrat dari nilai piksel. Kode menerima daftar nilai piksel sebagai input. Kemudian, untuk setiap nilai piksel, kode mengambil akar kuadrat dan mengembalikan daftar nilai piksel yang dinormalisasi.
import math
def normalize_pixels(pixels):
"""
Normalisasi nilai piksel dengan akar kuadrat.
"""
normalized_pixels = [math.sqrt(pixel) for pixel in pixels]
return normalized_pixels
# Contoh input:
pixel_values = [4, 9, 16, 25]
# Output:
print(normalize_pixels(pixel_values)) # Output: [2.0, 3.0, 4.0, 5.0]
Contoh 3: Model Pertumbuhan Eksponensial
Kode Python ini mensimulasikan pertumbuhan eksponensial. Kode menerima populasi awal, laju pertumbuhan, dan waktu sebagai input. Kode kemudian menghitung populasi pada waktu tertentu menggunakan rumus pertumbuhan eksponensial. Hasilnya adalah populasi pada waktu yang ditentukan.
import math
def exponential_growth(initial_population, growth_rate, time):
"""
Menghitung pertumbuhan eksponensial.
"""
population = initial_population
- math.exp(growth_rate
- time)
return population
# Contoh input:
initial_population = 100
growth_rate = 0.1
time = 5
# Output:
print(exponential_growth(initial_population, growth_rate, time)) # Output: 164.8721270700128
Daftar Aplikasi Teknologi
Berikut adalah tabel yang merangkum aplikasi teknologi yang menggunakan konsep akar dan pangkat:
| Bidang Teknologi | Contoh Aplikasi Spesifik | Bagaimana Akar/Pangkat Digunakan |
|---|---|---|
| Pemrosesan Gambar | Peningkatan Kontras, Deteksi Tepi | Normalisasi piksel, perhitungan gradien |
| Machine Learning | Regresi Logistik, Jaringan Saraf Tiruan | Fungsi aktivasi (sigmoid, ReLU), perhitungan loss function |
| Grafika Komputer | Rendering 3D, Pencahayaan | Perhitungan jarak, normalisasi vektor, transformasi geometri |
| Kriptografi | Enkripsi RSA | Operasi modular eksponensial |
| Analisis Data | Analisis Cluster, Analisis Regresi | Perhitungan jarak, fitting model |
| Pengembangan Game | Simulasi Fisika, Perhitungan Lintasan | Perhitungan gaya, gerakan objek, deteksi tumbukan |
| Sistem Rekomendasi | Sistem Rekomendasi Berbasis Kolaborasi | Perhitungan kesamaan (similarity), normalisasi skor |
| Pengolahan Suara | Pengenalan Ucapan, Kompresi Audio | Transformasi Fourier, perhitungan energi sinyal |
| Robotika | Perencanaan Gerakan, Navigasi | Perhitungan jarak, orientasi, kontrol motor |
| Keuangan | Perhitungan Bunga Majemuk, Analisis Risiko | Perhitungan pertumbuhan investasi, model risiko |
Studi Kasus Tambahan
Mari kita lihat studi kasus mendalam tentang penggunaan akar kuadrat dalam deteksi objek pada kamera pengawas. Sistem deteksi objek menggunakan algoritma untuk mengidentifikasi dan melacak objek dalam video. Salah satu langkah penting adalah mengidentifikasi piksel yang relevan dan mengelompokkannya menjadi objek. Algoritma seringkali menggunakan teknik seperti edge detection untuk menemukan tepi objek. Setelah tepi terdeteksi, algoritma menghitung jarak antara piksel untuk mengelompokkannya menjadi objek.
Akar kuadrat digunakan dalam perhitungan jarak antara piksel.
Tantangan:
- Performa: Algoritma deteksi objek harus berjalan secara real-time, yang berarti perhitungan harus cepat. Perhitungan akar kuadrat bisa memakan waktu.
- Noise: Gambar seringkali memiliki noise yang dapat mengganggu deteksi tepi.
Solusi yang Diterapkan:
- Optimasi Algoritma: Algoritma dioptimalkan untuk mengurangi jumlah perhitungan yang diperlukan. Misalnya, daripada menghitung jarak Euclidean penuh, beberapa algoritma menggunakan perkiraan jarak yang lebih cepat.
- Peningkatan Hardware: Penggunaan GPU (Graphics Processing Unit) untuk melakukan perhitungan paralel dapat mempercepat proses.
- Filter Noise: Filter seperti filter Gaussian digunakan untuk mengurangi noise dalam gambar sebelum deteksi tepi.
Dengan menggunakan akar kuadrat dalam perhitungan jarak, sistem dapat secara akurat mengidentifikasi dan melacak objek dalam video. Optimasi algoritma dan peningkatan hardware membantu memastikan bahwa sistem dapat berjalan secara real-time, bahkan dalam lingkungan yang kompleks.
Kesalahan Umum dan Cara Menghindarinya
Mengubah akar menjadi pangkat adalah keterampilan penting dalam matematika, namun seringkali siswa melakukan kesalahan yang dapat menyebabkan kebingungan dan jawaban yang salah. Memahami kesalahan umum ini dan cara menghindarinya sangat penting untuk menguasai konsep ini. Artikel ini akan membahas beberapa kesalahan yang paling sering terjadi, memberikan tips untuk menghindarinya, dan menyediakan kuis singkat untuk menguji pemahaman Anda.
Kesalahan dalam mengubah akar menjadi pangkat biasanya muncul akibat kurangnya pemahaman terhadap definisi dan sifat-sifat eksponen dan akar. Kesalahan ini dapat menyebabkan kesulitan dalam memecahkan soal matematika yang lebih kompleks. Mari kita bedah beberapa kesalahan umum dan bagaimana cara mengatasinya.
Kesalahan Umum dan Solusinya
Berikut adalah daftar kesalahan umum yang sering terjadi saat mengubah akar menjadi pangkat, beserta solusi untuk menghindarinya:
-
Kesalahan: Salah dalam mengidentifikasi indeks akar dan pangkat dari bilangan di dalam akar.
Solusi: Selalu perhatikan indeks akar (angka kecil di atas simbol akar) dan pangkat dari bilangan di dalam akar. Ingat bahwa
√x = x1/2
dan
n√x m = x m/n
Gunakan contoh soal untuk latihan.
-
Kesalahan: Mengabaikan tanda negatif pada bilangan di dalam akar.
Solusi: Jika bilangan di dalam akar memiliki tanda negatif, pastikan untuk mempertimbangkan hal ini saat mengubahnya menjadi pangkat. Perhatikan apakah indeks akar ganjil atau genap.
Jika indeks ganjil, tanda negatif tetap ada. Jika indeks genap, maka tidak terdefinisi dalam bilangan real, kecuali bilangan di dalam akar positif atau nol.
-
Kesalahan: Salah dalam menyederhanakan pecahan pangkat.
Solusi: Setelah mengubah akar menjadi pangkat, pastikan untuk menyederhanakan pecahan pangkat tersebut. Misalnya, 4√16 = 16 1/4 = (2 4) 1/4 = 2 1 = 2.
Latihan menyederhanakan pecahan adalah kunci.
-
Kesalahan: Tidak memahami urutan operasi matematika.
Solusi: Ingatlah urutan operasi matematika (PEMDAS/BODMAS): Kurung/Bracket, Eksponen/Orders, Perkalian dan Pembagian (dari kiri ke kanan), Penjumlahan dan Pengurangan (dari kiri ke kanan). Pastikan untuk mengikuti urutan operasi yang benar saat memecahkan soal yang melibatkan akar dan pangkat.
Kuis Singkat
Uji pemahaman Anda tentang konsep ini dengan kuis singkat berikut:
- Ubah √9 menjadi pangkat.
- Ubah 3√8 menjadi pangkat.
- Ubah 4√81 menjadi pangkat.
- Sederhanakan 16 1/2.
- Sederhanakan (-27) 1/3.
Sumber Belajar Tambahan
Memahami konsep mengubah akar menjadi pangkat memerlukan lebih dari sekadar membaca definisi dan rumus. Diperlukan latihan, eksplorasi, dan pemahaman yang mendalam. Untuk itu, beragam sumber belajar tambahan dapat menjadi kunci untuk menguasai materi ini. Berikut adalah daftar sumber belajar yang dapat membantu Anda memperdalam pengetahuan tentang akar dan pangkat, serta cara menggunakannya.
Sumber-sumber ini menawarkan pendekatan belajar yang berbeda, mulai dari buku teks yang komprehensif hingga platform interaktif yang menyenangkan. Dengan memanfaatkan berbagai sumber belajar, Anda dapat menemukan metode yang paling sesuai dengan gaya belajar Anda dan memaksimalkan pemahaman Anda tentang materi ini.
Perkaya Daftar Sumber Belajar
Untuk memperkaya pengalaman belajar, berikut adalah daftar sumber belajar tambahan yang bisa Anda manfaatkan. Sumber-sumber ini mencakup berbagai format, mulai dari buku teks hingga aplikasi interaktif, yang dirancang untuk memenuhi kebutuhan belajar yang beragam.
- Buku Teks Matematika SMA/SMK: Buku teks adalah sumber utama untuk mempelajari konsep akar dan pangkat secara sistematis. Buku teks biasanya menyediakan penjelasan yang jelas, contoh soal, dan latihan soal yang terstruktur.
- Website Edukasi Interaktif: Website seperti Khan Academy menawarkan video tutorial, latihan soal interaktif, dan kuis yang membantu Anda memahami konsep dengan cara yang lebih visual dan engaging.
- Kanal YouTube: Banyak kanal YouTube menyediakan video tutorial langkah demi langkah tentang akar dan pangkat. Video ini seringkali menampilkan visualisasi yang memudahkan pemahaman konsep yang kompleks.
- Aplikasi Belajar Matematika Berbasis Game: Aplikasi seperti Photomath atau aplikasi kuis matematika lainnya, mengubah belajar menjadi pengalaman yang lebih menyenangkan dan interaktif. Aplikasi ini seringkali menyediakan latihan soal yang bervariasi dan umpan balik instan.
Tabel Sumber Belajar yang Terstruktur
Berikut adalah tabel yang merangkum sumber belajar tambahan, beserta deskripsi dan tautan (jika tersedia):
| Sumber | Jenis | Deskripsi | Tautan |
|---|---|---|---|
| Khan Academy | Website | Menyediakan video tutorial, latihan soal interaktif, dan kuis tentang akar dan pangkat. Penjelasan mudah dipahami dan cocok untuk pemula. Kelebihan: gratis, akses mudah, materi terstruktur. Kekurangan: memerlukan koneksi internet. | https://www.khanacademy.org/ |
| Buku Matematika SMA Kelas X (contoh) | Buku Teks | Materi akar dan pangkat yang komprehensif, disertai contoh soal dan latihan. Cocok sebagai referensi utama. Kelebihan: materi lengkap, penjelasan detail. Kekurangan: mungkin memerlukan biaya. | (Sebutkan ISBN atau tautan pembelian) |
| YouTube (misalnya, channel “Zenius”) | Video Tutorial | Menyediakan video penjelasan konsep, contoh soal, dan pembahasan. Cocok untuk visual learner. Kelebihan: visual, mudah dipahami. Kekurangan: kualitas bervariasi, memerlukan koneksi internet. | (Cari channel YouTube matematika yang relevan) |
| Photomath | Aplikasi | Aplikasi yang dapat memecahkan soal matematika dengan memindai soal. Menunjukkan langkah-langkah penyelesaian. Kelebihan: instan, membantu memahami langkah-langkah. Kekurangan: tidak selalu akurat, bergantung pada kualitas foto soal. | (Unduh dari App Store atau Google Play) |
| Quipper School | Website | Menyediakan materi pembelajaran, latihan soal, dan kuis. Kelebihan: terstruktur, materi sesuai kurikulum. Kekurangan: mungkin berbayar. | (Cari Quipper School untuk materi matematika) |
Infografis Konseptual
Infografis adalah alat visual yang efektif untuk merangkum konsep kunci. Sebuah infografis tentang mengubah akar menjadi pangkat akan mencakup elemen-elemen berikut:
- Definisi Akar dan Pangkat: Penjelasan singkat dan jelas tentang apa itu akar (termasuk akar kuadrat, akar pangkat tiga, dan seterusnya) dan pangkat (eksponen).
- Hubungan Visual: Ilustrasi yang menunjukkan bagaimana akar dan pangkat saling berhubungan. Misalnya, diagram yang menunjukkan bagaimana akar kuadrat adalah kebalikan dari kuadrat.
- Rumus-Rumus Penting: Rumus-rumus dasar yang terkait dengan akar dan pangkat, seperti:
- a m/n = n√a m
- n√a
– n√b = n√(a*b) - (a m) n = a m*n
- Penyederhanaan Ekspresi: Contoh-contoh visual tentang bagaimana menyederhanakan ekspresi yang melibatkan akar dan pangkat. Ini bisa berupa langkah-langkah penyelesaian soal yang mudah diikuti.
- Desain Menarik: Penggunaan warna, ikon, dan tata letak yang menarik untuk membuat infografis mudah dipahami dan diingat.
Rekomendasi Latihan Soal
Latihan soal adalah kunci untuk menguasai konsep mengubah akar menjadi pangkat. Berikut adalah rekomendasi latihan soal:
- Jenis Soal:
- Pilihan Ganda: Untuk menguji pemahaman dasar dan kemampuan mengidentifikasi konsep yang benar.
- Isian Singkat: Untuk menguji kemampuan menghitung dan menerapkan rumus.
- Uraian: Untuk menguji kemampuan memecahkan masalah yang lebih kompleks dan menunjukkan langkah-langkah penyelesaian.
- Tingkat Kesulitan:
- Mudah: Soal-soal dasar yang menguji pemahaman konsep dasar.
- Sedang: Soal-soal yang memerlukan sedikit lebih banyak langkah penyelesaian dan penerapan rumus.
- Sulit: Soal-soal yang melibatkan kombinasi konsep dan memerlukan pemikiran kritis.
- Sumber Latihan Soal:
- Buku Latihan Soal: Banyak buku latihan soal matematika yang menyediakan soal-soal tentang akar dan pangkat.
- Website Penyedia Soal: Beberapa website menyediakan soal-soal latihan, kuis, dan tes online.
- Aplikasi: Beberapa aplikasi belajar matematika menawarkan latihan soal interaktif.
- Contoh Soal dan Kunci Jawaban:
- Soal: Ubah √25 menjadi bentuk pangkat.
- Kunci Jawaban: 25 1/2 atau 5
- Soal: Sederhanakan (2 3) 2.
- Kunci Jawaban: 2 6 atau 64
- Strategi Belajar:
- Kerjakan Soal Secara Bertahap: Mulailah dengan soal-soal mudah, lalu tingkatkan kesulitan secara bertahap.
- Periksa Jawaban: Selalu periksa jawaban Anda untuk memastikan pemahaman Anda benar.
- Analisis Kesalahan: Jika Anda salah, analisis di mana letak kesalahan Anda dan pelajari kembali konsep yang relevan.
- Latihan Teratur: Latihan secara teratur untuk memperkuat pemahaman dan kemampuan Anda.
Contoh Penerapan Konsep
Konsep akar dan pangkat memiliki banyak penerapan di berbagai bidang. Berikut adalah beberapa contoh:
Contoh: Perhitungan bunga majemuk dalam investasi menggunakan konsep pangkat. Rumus bunga majemuk adalah A = P(1 + r/n)nt, di mana A adalah jumlah akhir, P adalah modal awal, r adalah tingkat bunga, n adalah jumlah kali bunga dihitung per tahun, dan t adalah waktu (dalam tahun).
Contoh: Perhitungan jarak dalam fisika. Rumus jarak yang ditempuh oleh suatu benda yang bergerak dengan percepatan konstan melibatkan akar kuadrat.
Contoh: Dalam bidang komputer, akar kuadrat sering digunakan dalam algoritma untuk menghitung jarak antara dua titik dalam grafik.
Kiat Tambahan
Berikut adalah beberapa tips untuk memahami dan mengingat konsep akar dan pangkat dengan lebih mudah:
- Buat Catatan: Buat catatan singkat tentang rumus-rumus penting dan konsep-konsep kunci.
- Gunakan Visualisasi: Gunakan diagram, grafik, atau ilustrasi untuk membantu Anda memahami konsep secara visual.
- Latih Soal Secara Teratur: Semakin banyak Anda berlatih, semakin baik pemahaman Anda.
- Minta Bantuan: Jika Anda kesulitan, jangan ragu untuk meminta bantuan dari guru, teman, atau tutor.
- Hubungkan dengan Dunia Nyata: Cari contoh-contoh penerapan akar dan pangkat dalam kehidupan sehari-hari atau bidang yang Anda minati.
Penutupan
Menguasai ‘cara mengubah akar menjadi pangkat’ bukan hanya tentang memecahkan soal matematika; ini adalah tentang membangun fondasi yang kuat untuk pemahaman matematika yang lebih dalam. Dengan memahami konsep ini, Anda membuka pintu ke dunia aljabar, fisika, geometri, dan bahkan teknologi. Ingatlah, matematika adalah bahasa yang terus berkembang, dan dengan setiap konsep yang Anda kuasai, Anda semakin fasih dalam bahasa ini.
Teruslah berlatih, eksplorasi, dan jangan pernah berhenti bertanya. Selamat menjelajahi dunia matematika!
Pertanyaan yang Kerap Ditanyakan
Apa perbedaan utama antara akar dan pangkat?
Akar adalah operasi kebalikan dari pangkat. Pangkat menunjukkan berapa kali suatu bilangan dikalikan dengan dirinya sendiri, sementara akar mencari bilangan yang, jika dipangkatkan, akan menghasilkan bilangan asli.
Bagaimana cara mengubah akar kuadrat menjadi pangkat?
Akar kuadrat dari suatu bilangan (misalnya, √x) dapat diubah menjadi pangkat dengan eksponen 1/2 (x^(1/2)).
Apakah akar kubik juga bisa diubah menjadi pangkat?
Ya, akar kubik dari suatu bilangan (∛x) dapat diubah menjadi pangkat dengan eksponen 1/3 (x^(1/3)).
Bagaimana cara menangani akar dari variabel?
Akar dari variabel juga diubah menjadi bentuk pangkat dengan eksponen pecahan. Contoh: √x = x^(1/2), ∛x² = x^(2/3).
Apa saja kesalahan umum yang harus dihindari saat mengerjakan soal akar dan pangkat?
Kesalahan umum meliputi: salah mengaplikasikan aturan eksponen, lupa menyederhanakan, dan salah mengartikan notasi. Selalu periksa kembali pekerjaan Anda.
