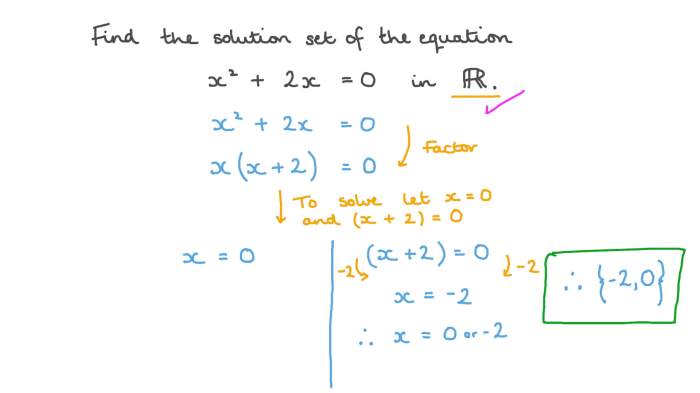Cara Mengerjakan Himpunan Penyelesaian: Panduan Langkah Demi Langkah

Himpunan penyelesaian adalah kumpulan nilai yang memenuhi suatu persamaan atau pertidaksamaan. Mengerjakan himpunan penyelesaian sangat penting dalam matematika dan memiliki berbagai aplikasi dalam kehidupan nyata. Artikel ini akan memberikan panduan langkah demi langkah tentang cara mengerjakan himpunan penyelesaian, termasuk jenis-jenisnya, operasi yang dapat dilakukan, dan kesalahan umum yang harus dihindari.

Table of Contents

Pengertian Himpunan Penyelesaian

Himpunan penyelesaian adalah sekumpulan semua nilai yang memenuhi suatu persamaan atau pertidaksamaan. Himpunan penyelesaian memainkan peran penting dalam aljabar, memungkinkan kita untuk menentukan solusi yang valid untuk persamaan atau pertidaksamaan yang diberikan.

Sebagai contoh, persamaan x+ 2 = 5 memiliki himpunan penyelesaian 3, karena menggantikan xdengan 3 menghasilkan persamaan yang benar. Demikian pula, pertidaksamaan x– 1 < 4 memiliki himpunan penyelesaian x| x < 5, yang merupakan semua nilai xyang kurang dari 5.

Mencari himpunan penyelesaian melibatkan penyederhanaan persamaan atau pertidaksamaan, mengisolasi variabel yang diinginkan, dan kemudian menentukan nilai yang memenuhi persamaan atau pertidaksamaan.

– Jelaskan langkah-langkah umum untuk menyelesaikan himpunan penyelesaian.

Langkah-langkah umum untuk menyelesaikan himpunan penyelesaian meliputi:

1. Isolasi variabel yang akan dipecahkan dengan melakukan operasi matematika pada kedua sisi persamaan. 2. Sederhanakan persamaan dengan menggabungkan istilah serupa dan melakukan operasi aritmatika. 3. Pecahkan persamaan untuk variabel yang diinginkan dengan menerapkan sifat-sifat kesetaraan. 4. Periksa solusi dengan mengganti nilai yang diperoleh ke dalam persamaan asli untuk memastikannya benar.

Metode Penyelesaian

Ada beberapa metode yang dapat digunakan untuk menyelesaikan himpunan penyelesaian, antara lain:

Isolasi variabel: Metode ini melibatkan pemindahan semua suku yang mengandung variabel yang akan dipecahkan ke satu sisi persamaan dan semua suku konstan ke sisi lainnya.
Faktorisasi: Metode ini melibatkan pemfaktoran sisi kiri persamaan menjadi dua atau lebih suku yang dapat dikalikan menjadi nol. Solusi diperoleh dengan menetapkan setiap faktor sama dengan nol dan menyelesaikan variabel.
Kuadrat sempurna: Metode ini digunakan ketika sisi kiri persamaan adalah kuadrat dari suatu suku. Suku tersebut dikalikan dengan dirinya sendiri dan persamaan diselesaikan dengan menggunakan metode pemfaktoran.

Tabel Metode Penyelesaian

Metode	Kelebihan	Kekurangan
Isolasi variabel	Mudah diterapkan	Dapat menjadi rumit untuk persamaan yang kompleks
Faktorisasi	Efektif untuk persamaan yang dapat difaktorkan	Tidak selalu memungkinkan untuk memfaktorkan semua persamaan
Kuadrat sempurna	Efektif untuk persamaan kuadrat sempurna	Hanya berlaku untuk persamaan kuadrat sempurna

Contoh Soal Terpecahkan

Isolasi variabel: Pecahkan persamaan 2x + 5 = 11 untuk x.

2x = 11 – 5 2x = 6 x = 6/2 x = 3

Faktorisasi: Pecahkan persamaan x^2 – 5x + 6 = 0 untuk x.

(x – 2)(x – 3) = 0 x – 2 = 0 atau x – 3 = 0 x = 2 atau x = 3

Kuadrat sempurna: Pecahkan persamaan (x – 5)^2 = 25 untuk x.

x – 5 = ±5 x = 5 ± 5 x = 10 atau x = 0

Cara Mengecek Jawaban

Setelah memperoleh himpunan penyelesaian, penting untuk mengecek jawaban dengan mengganti nilai yang diperoleh ke dalam persamaan asli. Jika persamaan menjadi benar, maka jawabannya valid.

Himpunan Penyelesaian Persamaan Linear

Persamaan linear adalah persamaan yang hanya memiliki pangkat satu dari variabel. Persamaan linear dapat digunakan untuk memodelkan berbagai situasi di dunia nyata, seperti gerak benda, pertumbuhan populasi, dan biaya.

Himpunan penyelesaian dari persamaan linear adalah himpunan semua nilai variabel yang memenuhi persamaan tersebut. Dengan kata lain, himpunan penyelesaian adalah himpunan semua nilai variabel yang membuat persamaan benar.

Mengisolasi Variabel

Untuk menemukan himpunan penyelesaian dari persamaan linear, kita perlu mengisolasi variabel pada satu sisi persamaan. Ini berarti kita perlu menyelesaikan persamaan untuk variabel.

Untuk mengisolasi variabel, kita dapat menggunakan operasi dasar berikut:

Menambahkan atau mengurangi angka yang sama pada kedua sisi persamaan
Mengalikan atau membagi kedua sisi persamaan dengan angka yang sama

Misalnya, untuk menyelesaikan persamaan 2x + 3 = 7, kita dapat menggunakan operasi dasar sebagai berikut:

Kurangi 3 dari kedua sisi persamaan: 2x + 3 – 3 = 7 – 3
Sederhanakan: 2x = 4
Bagi kedua sisi persamaan dengan 2: 2x/2 = 4/2
Sederhanakan: x = 2

Jadi, himpunan penyelesaian dari persamaan 2x + 3 = 7 adalah 2.

Menemukan Himpunan Penyelesaian

Setelah kita mengisolasi variabel, kita dapat menemukan himpunan penyelesaian dengan mensubstitusikan nilai variabel ke dalam persamaan aslinya.

Misalnya, untuk menemukan himpunan penyelesaian dari persamaan 2x + 3 = 7, kita dapat mensubstitusikan x = 2 ke dalam persamaan aslinya:

2(2) + 3 = 7

4 + 3 = 7

7 = 7

Karena persamaan tersebut benar, maka himpunan penyelesaian dari persamaan 2x + 3 = 7 adalah 2.

Himpunan Penyelesaian Persamaan Kuadrat

Persamaan kuadrat merupakan persamaan polinomial berderajat dua, yang memiliki bentuk umum ax²+ bx+ c= 0, dengan a, b, dan csebagai konstanta dan xsebagai variabel.

Metode Penyelesaian Himpunan Penyelesaian Persamaan Kuadrat

Faktorisasi

Jika persamaan kuadrat dapat difaktorkan menjadi dua bentuk linear, maka himpunan penyelesaiannya dapat ditemukan dengan menetapkan setiap faktor sama dengan nol.

Rumus Kuadrat

Rumus kuadrat digunakan untuk menemukan himpunan penyelesaian persamaan kuadrat yang tidak dapat difaktorkan. Rumusnya adalah:

x= (- b± √( b²– 4 ac)) / 2 a

Menyelesaikan Kuadrat Sempurna

Jika persamaan kuadrat dapat diselesaikan menjadi kuadrat sempurna, maka himpunan penyelesaiannya dapat ditemukan dengan mengambil akar kuadrat dari kedua sisi persamaan.

Himpunan Penyelesaian Pertidaksamaan Linear

Himpunan penyelesaian pertidaksamaan linear adalah kumpulan nilai variabel yang memenuhi pertidaksamaan tersebut. Menentukan himpunan penyelesaian sangat penting dalam matematika untuk memahami sifat-sifat dan solusi pertidaksamaan.

Langkah-langkah Menentukan Himpunan Penyelesaian

Isolasi Variabel:Isolasi variabel pada satu sisi pertidaksamaan dengan melakukan operasi matematika yang sama pada kedua sisi.
Tentukan Batas Solusi:Temukan nilai-nilai variabel yang membuat pertidaksamaan benar. Ini disebut batas solusi.
Buat Garis Bilangan:Buat garis bilangan dan tandai batas solusi.
Tentukan Solusi:Tentukan solusi pertidaksamaan dengan melihat bagian garis bilangan yang memenuhi pertidaksamaan.

Contoh

Misalkan kita memiliki pertidaksamaan 2x – 5< 10. Kita dapat menentukan himpunan penyelesaiannya sebagai berikut:

Isolasi Variabel:2x< 15
Tentukan Batas Solusi:x< 15/2 = 7,5
Buat Garis Bilangan:(Gambar garis bilangan dengan tanda 7,5 sebagai batas solusi)
Tentukan Solusi:Solusi adalah semua nilai x yang lebih kecil dari 7,5. Jadi, himpunan penyelesaiannya adalah x | x< 7,5.

Himpunan Penyelesaian Pertidaksamaan Kuadrat: Cara Mengerjakan Himpunan Penyelesaian

Pertidaksamaan kuadrat adalah persamaan kuadrat yang melibatkan tanda pertidaksamaan ( <, >, ≤, atau ≥). Himpunan penyelesaian dari pertidaksamaan kuadrat adalah nilai-nilai variabel yang memenuhi pertidaksamaan tersebut.

Cara mengerjakan himpunan penyelesaian tidak sesulit yang dibayangkan. Dengan memahami konsep dasar, kita dapat menyelesaikan soal-soal matematika dengan mudah. Misalnya, untuk menghilangkan kelopak mata berlipat, kita dapat menggunakan teknik blepharoplasty . Teknik ini melibatkan pemotongan kulit berlebih dan lemak di sekitar kelopak mata, sehingga menciptakan tampilan yang lebih muda dan segar.

Kembali ke topik himpunan penyelesaian, dengan menggunakan langkah-langkah sistematis, kita dapat menentukan himpunan solusi dari persamaan atau pertidaksamaan dengan tepat.

Ada beberapa metode untuk menyelesaikan himpunan penyelesaian pertidaksamaan kuadrat, yaitu menggunakan grafik, pengujian titik kritis, atau metode aljabar.

Grafik

Grafik fungsi kuadrat berbentuk parabola. Dengan membuat grafik fungsi kuadrat, kita dapat menentukan daerah yang memenuhi pertidaksamaan. Jika pertidaksamaannya adalah ≥ atau ≤, daerah yang memenuhi pertidaksamaan adalah area di bawah atau di atas parabola. Jika pertidaksamaannya adalah < atau >, daerah yang memenuhi pertidaksamaan adalah area di luar parabola.

Pengujian Titik Kritis

Titik kritis dari fungsi kuadrat adalah titik di mana turunan pertama sama dengan nol. Dengan menguji tanda turunan pertama di sekitar titik kritis, kita dapat menentukan daerah yang memenuhi pertidaksamaan. Jika turunan pertama positif, fungsi kuadrat meningkat, dan jika turunan pertama negatif, fungsi kuadrat menurun.

Metode Aljabar

Metode aljabar untuk menyelesaikan himpunan penyelesaian pertidaksamaan kuadrat melibatkan penyelesaian persamaan kuadrat yang dihasilkan dengan menyamakan fungsi kuadrat dengan nol. Dengan menggunakan teorema nilai nol, kita dapat menemukan akar-akar fungsi kuadrat dan menentukan daerah yang memenuhi pertidaksamaan.

Kelebihan dan Kekurangan Setiap Metode

Metode	Kelebihan	Kekurangan
Grafik	Visualisasi yang jelas	Sulit untuk mendapatkan solusi yang tepat
Pengujian Titik Kritis	Mudah diterapkan	Dapat memberikan solusi yang tidak tepat
Metode Aljabar	Memberikan solusi yang tepat	Proses perhitungan yang lebih kompleks

Poin Penting yang Perlu Diingat:

Himpunan penyelesaian pertidaksamaan kuadrat dapat ditentukan menggunakan grafik, pengujian titik kritis, atau metode aljabar.

Grafik fungsi kuadrat berbentuk parabola.

Titik kritis adalah titik di mana turunan pertama sama dengan nol.

Metode aljabar memberikan solusi yang tepat, tetapi proses perhitungannya lebih kompleks.

Untuk mempelajari lebih lanjut tentang himpunan penyelesaian pertidaksamaan kuadrat, Anda dapat merujuk ke sumber daya berikut:

Himpunan Penyelesaian Sistem Persamaan

Dalam matematika, himpunan penyelesaian sistem persamaan adalah sekumpulan semua nilai variabel yang memenuhi setiap persamaan dalam sistem tersebut. Sistem persamaan adalah kumpulan dua atau lebih persamaan yang melibatkan variabel yang sama. Menemukan himpunan penyelesaian sangat penting untuk memahami hubungan antara variabel dan memecahkan masalah yang melibatkan sistem persamaan.

Metode Substitusi

Metode substitusi adalah salah satu metode yang paling umum digunakan untuk menyelesaikan himpunan penyelesaian. Dalam metode ini, kita mengganti salah satu variabel dalam satu persamaan dengan ekspresi yang setara dari variabel tersebut dalam persamaan lainnya. Dengan cara ini, kita dapat mengurangi sistem menjadi satu persamaan dalam satu variabel, yang kemudian dapat kita selesaikan.

Metode Eliminasi

Metode eliminasi adalah metode lain yang dapat digunakan untuk menyelesaikan himpunan penyelesaian. Dalam metode ini, kita mengalikan kedua sisi persamaan dengan konstanta sehingga koefisien salah satu variabel menjadi sama. Kemudian, kita menjumlahkan atau mengurangkan persamaan yang dihasilkan untuk menghilangkan salah satu variabel.

Dengan cara ini, kita dapat mengurangi sistem menjadi satu persamaan dalam satu variabel, yang kemudian dapat kita selesaikan.

Metode Matriks

Metode matriks adalah metode yang lebih umum yang dapat digunakan untuk menyelesaikan sistem persamaan dengan dua atau lebih variabel. Dalam metode ini, kita menulis sistem persamaan dalam bentuk matriks dan kemudian menggunakan operasi matriks untuk menemukan himpunan penyelesaian. Metode matriks sangat efisien untuk menyelesaikan sistem persamaan yang besar atau kompleks.

Kesimpulan

Menemukan himpunan penyelesaian sistem persamaan adalah keterampilan penting dalam matematika. Ada beberapa metode yang dapat digunakan untuk menyelesaikan himpunan penyelesaian, termasuk metode substitusi, eliminasi, dan matriks. Metode yang digunakan tergantung pada sistem persamaan yang diberikan dan preferensi individu.

Cara Menyelesaikan Himpunan Penyelesaian Sistem Pertidaksamaan Linear Dua Variabel

Sistem pertidaksamaan linear dua variabel terdiri dari dua atau lebih pertidaksamaan yang memuat dua variabel. Untuk menyelesaikan sistem ini, kita perlu menemukan semua pasangan nilai variabel yang memenuhi semua pertidaksamaan secara bersamaan.

Menggambar Grafik

Untuk menyelesaikan sistem pertidaksamaan, kita bisa menggambar grafik dari setiap pertidaksamaan pada bidang koordinat. Batas grafik adalah garis yang memisahkan area solusi dari area non-solusi.

Menentukan Solusi

Setelah menggambar grafik, kita perlu menentukan solusi yang memenuhi semua pertidaksamaan. Area yang memenuhi semua pertidaksamaan disebut daerah penyelesaian atau himpunan penyelesaian.

Menggunakan Garis Uji

Untuk menentukan daerah penyelesaian, kita dapat menggunakan garis uji. Garis uji adalah garis lurus yang sejajar dengan salah satu sumbu koordinat. Kita menggerakkan garis uji sampai menyentuh batas-batas grafik. Titik potong garis uji dengan batas grafik menunjukkan solusi yang memenuhi pertidaksamaan.

Menulis Himpunan Penyelesaian

Himpunan penyelesaian adalah kumpulan semua solusi yang memenuhi sistem pertidaksamaan. Himpunan ini dapat ditulis dalam notasi himpunan menggunakan kurung kurawal . Misalnya, himpunan penyelesaian (x, y) | x > 2, y < 5 mewakili semua pasangan nilai (x, y) yang memenuhi x lebih besar dari 2 dan y kurang dari 5.

Pentingnya Menyelesaikan Sistem Pertidaksamaan

Menyelesaikan sistem pertidaksamaan sangat penting dalam berbagai aplikasi dunia nyata, seperti:

Optimasi

Menemukan nilai variabel yang memaksimalkan atau meminimalkan fungsi tertentu.

Pembatasan

Memastikan bahwa solusi memenuhi persyaratan atau batasan tertentu.

Perencanaan

Membuat keputusan berdasarkan kendala atau preferensi yang berbeda.

Menyelesaikan himpunan penyelesaian merupakan tugas yang menantang, tetapi dengan langkah sistematis, kita dapat mengatasinya. Setelah mengidentifikasi himpunan semesta dan himpunan bagian, kita dapat menggunakan operasi himpunan untuk menemukan irisan, gabungan, selisih, dan komplemennya. Sama seperti menghapus ulasan negatif di Google Maps, prosesnya memerlukan pendekatan yang komprehensif.

Untuk panduan lengkap tentang cara menghapus ulasan negatif, silakan kunjungi Hapus Ulasan Negatif di Google Maps: Panduan Lengkap . Setelah memperoleh solusi untuk himpunan penyelesaian, kita dapat memperoleh wawasan berharga dari hubungan antar himpunan.

– Jelaskan konsep himpunan penyelesaian dan berikan contoh dalam konteks matematika.

Dalam matematika, himpunan penyelesaian adalah kumpulan semua nilai yang memenuhi persamaan atau sistem persamaan. Himpunan penyelesaian dapat ditentukan dengan berbagai metode, seperti substitusi, eliminasi, atau pemfaktoran.

Contohnya, misalkan kita memiliki persamaan x + 2 = 5. Himpunan penyelesaiannya adalah 3, karena ketika kita mengganti x dengan 3, persamaannya menjadi benar: 3 + 2 = 5.

Aplikasi Himpunan Penyelesaian dalam Fisika

Dalam fisika, himpunan penyelesaian digunakan untuk menghitung lintasan suatu benda. Misalnya, jika kita memiliki benda yang dilempar vertikal ke atas dengan kecepatan awal v, maka persamaan lintasannya adalah:

h = vt – 1/2 gt^2

di mana h adalah tinggi benda pada waktu t, g adalah percepatan gravitasi, dan v adalah kecepatan awal benda.

Untuk menentukan waktu yang dibutuhkan benda untuk mencapai ketinggian tertentu, kita dapat menyelesaikan persamaan ini untuk t. Himpunan penyelesaian persamaan tersebut akan memberikan waktu yang dibutuhkan benda untuk mencapai ketinggian tersebut.

Aplikasi Himpunan Penyelesaian dalam Ekonomi

Dalam ekonomi, himpunan penyelesaian digunakan untuk menentukan titik keseimbangan pasar. Titik keseimbangan pasar adalah harga dan kuantitas di mana penawaran dan permintaan berada dalam keseimbangan.

Misalkan kita memiliki fungsi penawaran Qs = 2P dan fungsi permintaan Qd = 10 – P. Untuk menentukan titik keseimbangan pasar, kita dapat menyelesaikan kedua persamaan ini untuk P.

Untuk menguasai cara mengerjakan himpunan penyelesaian, penting untuk memahami konsep dasarnya terlebih dahulu. Setelah memahami konsepnya, kamu dapat memanfaatkan Tutorial untuk mengasah keterampilanmu. Tutorial ini akan memandu kamu langkah demi langkah dalam mengerjakan berbagai jenis himpunan penyelesaian. Dengan mengikuti langkah-langkah yang tepat dan berlatih secara teratur, kamu akan semakin mahir dalam mengerjakan himpunan penyelesaian.

Himpunan penyelesaian kedua persamaan ini akan memberikan harga keseimbangan pasar.

Aplikasi Himpunan Penyelesaian di Bidang Lainnya, Cara mengerjakan himpunan penyelesaian

Bidang	Contoh Aplikasi
Kimia	Menentukan konsentrasi suatu zat dalam reaksi kimia
Biologi	Menghitung pertumbuhan populasi
Teknik	Merancang struktur yang tahan gempa

Dengan menggunakan himpunan penyelesaian, kita dapat menyelesaikan masalah dunia nyata di berbagai bidang. Himpunan penyelesaian sangat penting untuk memahami dan memprediksi perilaku sistem dalam berbagai disiplin ilmu.

Himpunan penyelesaian adalah alat yang ampuh untuk memecahkan masalah praktis. Dengan menentukan himpunan penyelesaian persamaan atau sistem persamaan, kita dapat memperoleh informasi penting tentang sistem yang sedang dipelajari.

Referensi:

Kesalahan Umum dalam Menyelesaikan Himpunan Penyelesaian

Menyelesaikan himpunan penyelesaian adalah keterampilan penting dalam matematika. Namun, siswa sering melakukan kesalahan yang dapat menghambat pemahaman mereka. Memahami kesalahan umum ini dan cara menghindarinya sangat penting untuk meningkatkan akurasi dan pemahaman siswa.

Mengabaikan Kondisi

Salah satu kesalahan umum adalah mengabaikan kondisi yang diberikan dalam soal. Kondisi ini membatasi nilai variabel yang dapat diterima sebagai solusi. Misalnya, jika soal menyatakan “x > 0”, siswa harus memastikan bahwa solusi yang mereka temukan memenuhi kondisi ini. Mengabaikan kondisi dapat menyebabkan solusi yang tidak valid.

Untuk menyelesaikan himpunan penyelesaian, kita harus menentukan nilai yang memenuhi persamaan. Seperti halnya mencari uang di Spotify, kita perlu menemukan cara untuk menghasilkan pendapatan melalui platform ini. Spotify menawarkan berbagai metode untuk memonetisasi konten, seperti mendapatkan royalti dari streaming , menjadi afiliasi, atau menjual merchandise.

Dengan memahami persamaan dan mengidentifikasi metode yang tepat, kita dapat memperoleh penghasilan dari himpunan penyelesaian dan Spotify.

Menggunakan Operasi yang Salah

Kesalahan umum lainnya adalah menggunakan operasi yang salah saat menyelesaikan persamaan atau pertidaksamaan. Misalnya, siswa mungkin secara tidak sengaja mengurangkan alih-alih menambah, atau membagi alih-alih mengalikan. Menggunakan operasi yang salah dapat menghasilkan solusi yang salah.

Membagi dengan Nol

Membagi dengan nol adalah kesalahan serius yang dapat membuat penyelesaian tidak valid. Saat menyelesaikan pertidaksamaan, siswa harus memastikan bahwa penyebut tidak sama dengan nol. Membagi dengan nol dapat menyebabkan hasil yang tidak terdefinisi atau tak hingga.

Menggunakan Nilai Negatif untuk Akar Kuadrat

Akar kuadrat dari angka positif selalu positif. Kesalahan umum adalah menggunakan nilai negatif untuk akar kuadrat dari angka positif. Ini dapat menyebabkan solusi yang salah atau tidak valid.

Mengabaikan Solusi Ekstrinsik

Saat menyelesaikan pertidaksamaan, penting untuk memeriksa solusi ekstrinsik. Solusi ekstrinsik adalah solusi yang memenuhi pertidaksamaan tetapi tidak memenuhi kondisi yang diberikan. Mengabaikan solusi ekstrinsik dapat menyebabkan kesimpulan yang salah.

Sumber Daya Tambahan untuk Mempelajari Himpunan Penyelesaian

Untuk memperluas pengetahuan Anda tentang himpunan penyelesaian, berikut beberapa sumber daya tambahan yang dapat Anda manfaatkan:

Buku Teks

Matematika untuk Sekolah Menengah Atas oleh Muslimin dan Asmarani
Himpunan Penyelesaian oleh Drs. Hartono
Algebra Dasar oleh Prof. Dr. A. Buchori

Situs Web

Video Tutorial

Contoh Soal dan Solusi

Untuk memahami konsep himpunan penyelesaian, kita akan membahas beberapa contoh soal beserta langkah-langkah penyelesaiannya. Soal-soal ini mencakup berbagai jenis persamaan dan pertidaksamaan, serta menunjukkan penerapan sifat-sifat persamaan dan pertidaksamaan.

Soal 1: Persamaan Linear Satu Variabel

Selesaikan persamaan berikut untuk x:

2x + 5 = 11

Langkah 1: Kurangi 5 dari kedua sisi persamaan

2x + 5 – 5 = 11 – 5

2x = 6

Langkah 2: Bagi kedua sisi persamaan dengan 2

(2x) / 2 = 6 / 2

x = 3

Himpunan Penyelesaian: 3

Untuk menyelesaikan himpunan penyelesaian suatu persamaan, kita perlu memahami konsep-konsep dasar aljabar. Persamaan adalah suatu pernyataan yang menyatakan bahwa dua ekspresi matematika adalah sama. Salah satu cara mengerjakan himpunan penyelesaian adalah dengan memindahkan semua suku yang mengandung variabel ke satu sisi persamaan dan suku-suku konstanta ke sisi lainnya.

Setelah itu, kita dapat menyelesaikan variabel dengan melakukan operasi matematika sederhana. Nah, tahukah kamu? Selain mengerjakan soal matematika, kamu juga bisa dengan mudah mengirim uang dari PayPal ke DANA. Cara Mudah Kirim Uang dari PayPal ke DANA sangat praktis dan hanya membutuhkan beberapa langkah saja.

Kembali ke topik himpunan penyelesaian, setelah mendapatkan nilai variabel, kita telah menyelesaikan himpunan penyelesaian persamaan tersebut.

Rangkuman Poin-Poin Penting

Berikut ini adalah rangkuman poin-poin penting tentang cara mengerjakan himpunan penyelesaian:

Himpunan penyelesaian adalah kumpulan semua nilai yang memenuhi persamaan atau pertidaksamaan tertentu. Untuk mengerjakan himpunan penyelesaian, ada beberapa langkah yang dapat diikuti:

Langkah 1: Ubah Persamaan ke Bentuk Standar

Ubah persamaan ke bentuk standar dengan mengisolasi variabel pada satu sisi persamaan. Misalnya, untuk persamaan 2x + 5 = 11, kurangi 5 dari kedua sisi untuk mendapatkan 2x = 6.

Langkah 2: Bagi Kedua Sisi dengan Koefisien Variabel

Bagi kedua sisi persamaan dengan koefisien variabel. Dalam contoh sebelumnya, bagi kedua sisi dengan 2 untuk mendapatkan x = 3.

Langkah 3: Periksa Solusi

Ganti nilai yang diperoleh ke dalam persamaan asli untuk memeriksa apakah itu benar-benar merupakan solusi. Dalam contoh ini, ganti x dengan 3 ke dalam 2x + 5 = 11 menghasilkan 2(3) + 5 = 11, yang benar.

Langkah 4: Tulis Himpunan Penyelesaian

Tulis himpunan penyelesaian dalam bentuk x | x = nilai yang diperoleh. Dalam contoh ini, himpunan penyelesaiannya adalah x | x = 3.

Tips dan Trik

Gunakan kalkulator atau alat aljabar untuk menyelesaikan persamaan yang rumit.
Perhatikan tanda-tanda pertidaksamaan saat menyelesaikan pertidaksamaan.
Latih secara teratur untuk meningkatkan keterampilan mengerjakan himpunan penyelesaian.

Ringkasan Terakhir

Mengerjakan himpunan penyelesaian adalah keterampilan penting yang dapat membantu Anda memecahkan masalah, membuat keputusan, dan memahami berbagai konsep matematika. Dengan mengikuti langkah-langkah yang diuraikan dalam artikel ini, Anda dapat menguasai teknik ini dan menjadi ahli dalam menyelesaikan himpunan penyelesaian.

Panduan Pertanyaan dan Jawaban

Apa itu himpunan penyelesaian?

Himpunan penyelesaian adalah kumpulan semua nilai yang membuat persamaan atau pertidaksamaan menjadi benar.

Bagaimana cara mengerjakan himpunan penyelesaian persamaan linear?

Isolasi variabel pada satu sisi persamaan dan selesaikan untuk variabel tersebut.

Apa saja jenis-jenis himpunan penyelesaian?

Himpunan kosong, himpunan tunggal, himpunan terbatas, dan himpunan tak terbatas.

Post Views: 141