Cara operasi hitung bilangan bulat – Dalam dunia matematika, operasi hitung bilangan bulat merupakan landasan penting yang membuka pintu bagi pemahaman yang lebih mendalam tentang konsep numerik. Dari transaksi keuangan hingga perhitungan ilmiah, operasi hitung bilangan bulat memainkan peran penting dalam kehidupan kita sehari-hari.
Panduan komprehensif ini akan membawa Anda melalui seluk-beluk operasi hitung bilangan bulat, memberikan pemahaman yang jelas tentang konsep dasar, prosedur langkah demi langkah, dan aplikasi praktisnya. Mari selami dunia bilangan bulat dan kuasai seni operasi hitungnya.
Definisi Operasi Hitung Bilangan Bulat
Operasi hitung bilangan bulat merupakan tindakan aritmatika yang dilakukan pada bilangan bulat, yaitu bilangan yang tidak memiliki komponen pecahan atau desimal. Operasi dasar meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Contoh operasi hitung bilangan bulat:
- Penjumlahan: 5 + 7 = 12
- Pengurangan: 10 – 3 = 7
- Perkalian: 4 x 6 = 24
- Pembagian: 15 ÷ 5 = 3
Sifat Operasi Hitung Bilangan Bulat
Operasi hitung bilangan bulat memiliki beberapa sifat penting, yaitu:
- Komutatif:Urutan bilangan tidak memengaruhi hasil penjumlahan atau perkalian. (a + b = b + a) dan (a x b = b x a)
- Asosiatif:Pengelompokan bilangan tidak memengaruhi hasil penjumlahan atau perkalian. (a + (b + c) = (a + b) + c) dan (a x (b x c) = (a x b) x c)
- Distributif:Perkalian memiliki prioritas lebih tinggi daripada penjumlahan atau pengurangan. (a x (b + c) = a x b + a x c)
Prosedur Operasi Hitung Bilangan Bulat
Operasi hitung bilangan bulat merupakan dasar dari matematika dan banyak aplikasi praktis. Operasi dasar meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan dan Pengurangan
Penjumlahan bilangan bulat melibatkan penggabungan dua atau lebih bilangan bulat untuk menghasilkan jumlahnya. Pengurangan, sebaliknya, melibatkan pengambilan satu bilangan bulat dari yang lain untuk menghasilkan selisihnya. Dalam kedua operasi ini, tanda bilangan bulat (positif atau negatif) sangat penting.
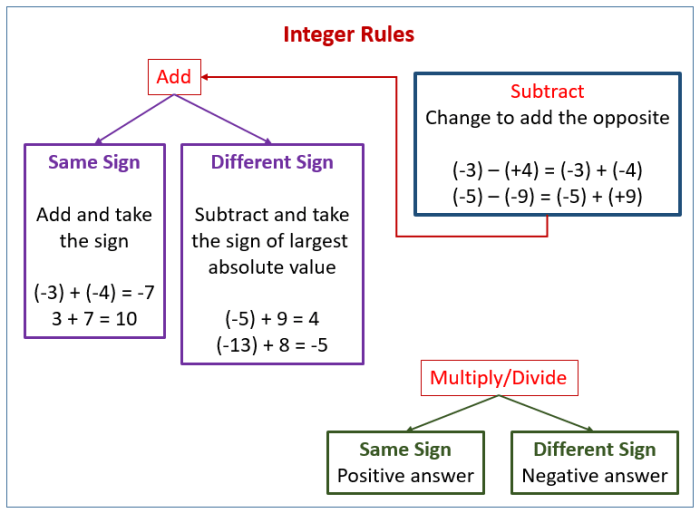
- Jika kedua bilangan bulat bertanda sama (positif atau negatif), tanda hasilnya sama.
- Jika kedua bilangan bulat berlawanan tanda, tanda hasilnya positif jika bilangan bulat positif lebih besar dan negatif jika bilangan bulat negatif lebih besar.
Perkalian dan Pembagian
Perkalian bilangan bulat melibatkan pengulangan penjumlahan satu bilangan bulat dengan dirinya sendiri sebanyak yang ditentukan oleh bilangan bulat lainnya. Pembagian, sebaliknya, melibatkan pembagian satu bilangan bulat dengan yang lain untuk menghasilkan hasil bagi dan sisa.
- Tanda hasil perkalian dua bilangan bulat bergantung pada tanda kedua bilangan bulat tersebut: positif jika keduanya sama dan negatif jika berlawanan.
- Tanda hasil bagi dua bilangan bulat bergantung pada tanda kedua bilangan bulat tersebut: positif jika keduanya sama dan negatif jika berlawanan. Sisa memiliki tanda yang sama dengan pembaginya.
Contoh
Mari kita perhatikan beberapa contoh:
- Penjumlahan: 5 + (-3) = 2 (bilangan bulat positif lebih besar)
- Pengurangan: 10 – 7 = 3 (bilangan bulat positif lebih besar)
- Perkalian: (-4) x 5 = -20 (tanda negatif karena kedua bilangan bulat negatif)
- Pembagian: 15 ÷ (-3) = -5 (hasil bagi negatif karena pembagi dan dividen berlawanan tanda)
Aturan Operasi
Aturan operasi adalah seperangkat aturan yang mengatur urutan operasi hitung bilangan bulat. Aturan ini memastikan bahwa semua orang mendapatkan hasil yang sama saat melakukan operasi hitung yang sama, sehingga menghindari kebingungan dan kesalahan.
Urutan Operasi
Urutan operasi hitung bilangan bulat adalah sebagai berikut:
- Tanda kurung
- Eksponen
- Perkalian dan pembagian (dari kiri ke kanan)
- Penjumlahan dan pengurangan (dari kiri ke kanan)
Ketika ada beberapa operasi dengan tingkat prioritas yang sama (misalnya, perkalian dan pembagian), operasi tersebut dikerjakan dari kiri ke kanan.
Contoh
Sebagai contoh, mari kita selesaikan operasi hitung berikut:
2 + 3 × 4- 5
Mengikuti urutan operasi, kita kerjakan dulu operasi dalam tanda kurung (tidak ada dalam kasus ini), kemudian eksponen (tidak ada), kemudian perkalian dan pembagian (dari kiri ke kanan), dan terakhir penjumlahan dan pengurangan (dari kiri ke kanan).
Jadi, kita kerjakan 3 × 4terlebih dahulu, yang menghasilkan 12. Kemudian, kita kerjakan 2 + 12, yang menghasilkan 14. Terakhir, kita kerjakan 14- 5 , yang menghasilkan 9.
Jadi, hasil akhir dari operasi hitung tersebut adalah 9.
Kesalahan Umum
Kesalahan umum yang dilakukan saat menggunakan aturan operasi meliputi:
- Melupakan tanda kurung
- Mengerjakan operasi dengan prioritas yang sama dari kanan ke kiri
- Mengabaikan tanda negatif
Untuk menghindari kesalahan ini, penting untuk mengikuti aturan operasi dengan hati-hati.
Mengabaikan aturan operasi dapat menyebabkan hasil perhitungan yang salah, sehingga penting untuk mengikutinya dengan cermat.
Operasi hitung bilangan bulat merupakan dasar dari komputasi digital. Setiap komputer modern menggunakan operasi ini untuk melakukan perhitungan. Yang menarik, prinsip yang sama juga digunakan dalam cara kerja machine learning . Algoritma machine learning dilatih dengan data numerik, dan mereka belajar dengan mengoperasikan data tersebut dengan cara yang mirip dengan cara operasi hitung bilangan bulat.
Dengan memahami prinsip dasar operasi hitung bilangan bulat, kita dapat lebih menghargai kompleksitas dan kekuatan machine learning.
Operasi Penjumlahan Bilangan Bulat
Dalam matematika, operasi penjumlahan pada bilangan bulat merupakan konsep dasar yang melibatkan penambahan dua atau lebih bilangan bulat untuk menghasilkan bilangan bulat baru. Bilangan bulat adalah bilangan yang dapat ditulis tanpa bagian desimal, termasuk bilangan positif, negatif, dan nol.
Penjumlahan bilangan bulat mengikuti aturan tertentu yang didasarkan pada tanda kedua bilangan yang dijumlahkan. Tabel berikut merangkum aturan tersebut:
Aturan Penjumlahan Bilangan Bulat
| Bilangan 1 | Bilangan 2 | Hasil |
|---|---|---|
| Positif | Positif | Positif |
| Negatif | Negatif | Negatif |
| Positif | Negatif | Positif atau negatif (tergantung mana yang lebih besar) |
| Negatif | Positif | Positif atau negatif (tergantung mana yang lebih besar) |
Sebagai contoh, jika kita menjumlahkan bilangan bulat 5 dan 3, hasilnya adalah 8 karena kedua bilangan tersebut positif. Sebaliknya, jika kita menjumlahkan -5 dan -3, hasilnya adalah -8 karena kedua bilangan tersebut negatif. Terakhir, jika kita menjumlahkan 5 dan -3, hasilnya adalah 2 karena bilangan positif (5) lebih besar dari bilangan negatif (-3).
Operasi Pengurangan Bilangan Bulat
Pengurangan bilangan bulat adalah operasi matematika yang mengurangkan satu bilangan bulat dari bilangan bulat lainnya. Dalam operasi ini, bilangan bulat yang dikurangi disebut minuend, sedangkan bilangan bulat yang dikurangkan disebut subtrahend. Hasil pengurangan disebut selisih.
Aturan Pengurangan Bilangan Bulat
- Jika minuend dan subtrahend bertanda sama (keduanya positif atau negatif), kurangi nilai absolut subtrahend dari nilai absolut minuend. Tanda selisih sama dengan tanda minuend.
- Jika minuend dan subtrahend bertanda berbeda, jumlahkan nilai absolut minuend dan subtrahend. Tanda selisih sama dengan tanda bilangan bulat yang lebih besar.
Contoh Pengurangan Bilangan Bulat
Contoh Sederhana
Kurangkan -5 dari 10.
Minuend: 10
Subtrahend: -5
Operasi hitung bilangan bulat mengikuti aturan tertentu untuk menghitung hasil yang akurat. Misalnya, ketika menjumlahkan dua bilangan positif, hasilnya selalu positif. Namun, dalam dunia komunikasi digital, ada juga aturan yang perlu dipahami, seperti cara menonaktifkan saluran di WhatsApp. Dengan mengikuti langkah-langkah yang tertera di sini , Anda dapat mengontrol saluran yang ingin diaktifkan atau dinonaktifkan, memastikan kenyamanan dan privasi dalam berkomunikasi.
Kembali ke operasi hitung bilangan bulat, memahami aturan-aturan ini sangat penting untuk melakukan perhitungan yang benar dan menghindari kesalahan.
Karena minuend dan subtrahend bertanda berbeda, kita jumlahkan nilai absolutnya: 10 + 5 = 15.
Tanda selisih sama dengan tanda bilangan bulat yang lebih besar, yaitu positif. Jadi, selisihnya adalah 15.
Contoh Kompleks
Kurangkan -12 dari -7.
Minuend: -7
Subtrahend: -12
Karena minuend dan subtrahend bertanda sama (negatif), kita kurangi nilai absolut subtrahend dari nilai absolut minuend: 7 – 12 = -5.
Tanda selisih sama dengan tanda minuend, yaitu negatif. Jadi, selisihnya adalah -5.
Operasi Perkalian Bilangan Bulat
Dalam matematika, perkalian bilangan bulat adalah operasi matematika yang menggabungkan dua bilangan bulat, yang disebut faktor, untuk menghasilkan bilangan bulat baru, yang disebut hasil kali. Perkalian bilangan bulat mengikuti aturan khusus yang bergantung pada tanda kedua faktor.
Konsep Perkalian Bilangan Bulat, Cara operasi hitung bilangan bulat
- Jika kedua faktor positif, hasil kali juga positif.
- Jika salah satu faktor negatif dan yang lainnya positif, hasil kali negatif.
- Jika kedua faktor negatif, hasil kali positif.
Tabel Aturan Perkalian Bilangan Bulat
| Faktor 1 | Faktor 2 | Hasil Kali |
|---|---|---|
| + | + | + |
| + | – | – |
| – | + | – |
| – | – | + |
Contoh Perkalian Bilangan Bulat
Contoh sederhana:
- 5 x 3 = 15 (kedua faktor positif)
- -2 x 4 = -8 (salah satu faktor negatif)
Contoh kompleks:
- (-3) x (-5) = 15 (kedua faktor negatif)
- 6 x (-2) x (-1) = 12 (dua faktor negatif dan satu faktor positif)
Langkah-langkah Perkalian Bilangan Bulat
- Tentukan tanda hasil kali berdasarkan aturan perkalian.
- Abaikan tanda faktor dan kalikan nilai absolutnya.
- Beri tanda hasil kali sesuai dengan aturan perkalian.
Contoh Soal Perkalian Bilangan Bulat
Hitunglah hasil dari (-4) x (-6) x 3.
- Tanda hasil kali: positif (dua faktor negatif dan satu faktor positif)
- Nilai absolut: 4 x 6 x 3 = 72
- Hasil kali: 72
Sifat Komutatif dan Asosiatif
- Sifat komutatif:Perkalian bilangan bulat bersifat komutatif, artinya urutan faktor tidak memengaruhi hasil kali.
- Sifat asosiatif:Perkalian bilangan bulat bersifat asosiatif, artinya pengelompokan faktor tidak memengaruhi hasil kali.
Penggunaan Perkalian Bilangan Bulat dalam Kehidupan Sehari-hari
- Menghitung luas dan volume bentuk geometris
- Menghitung kecepatan dan jarak dalam fisika
- Membuat perhitungan keuangan, seperti bunga dan investasi
Operasi Pembagian Bilangan Bulat
Pembagian bilangan bulat adalah operasi matematika yang melibatkan pembagian satu bilangan bulat (pembagi) dengan bilangan bulat lainnya (pembagi). Hasilnya adalah bilangan bulat yang menunjukkan berapa kali pembagi dapat dimasukkan ke dalam pembagi.
Aturan Pembagian Bilangan Bulat
Berikut adalah aturan pembagian bilangan bulat:
- Jika pembagi dan pembagi memiliki tanda yang sama (keduanya positif atau keduanya negatif), hasilnya positif.
- Jika pembagi dan pembagi memiliki tanda yang berbeda (satu positif dan satu negatif), hasilnya negatif.
- Jika pembagi adalah 0, hasilnya tidak terdefinisi.
Contoh Pembagian Bilangan Bulat
Berikut adalah beberapa contoh pembagian bilangan bulat:
- 10 ÷ 5 = 2 (keduanya positif, hasilnya positif)
- -12 ÷ 4 = -3 (keduanya negatif, hasilnya positif)
- 15 ÷ (-3) = -5 (satu positif, satu negatif, hasilnya negatif)
- 20 ÷ 0 tidak terdefinisi (pembagi adalah 0)
Contoh Soal Operasi Hitung Bilangan Bulat: Cara Operasi Hitung Bilangan Bulat
Setelah memahami aturan operasi hitung bilangan bulat, kini saatnya mengasah pemahaman Anda melalui beberapa contoh soal. Berikut adalah beberapa contoh soal operasi hitung bilangan bulat dengan tingkat kesulitan yang bervariasi:
Soal 1
Hitunglah: 5 + (-3)
Langkah Penyelesaian:
- Perhatikan bahwa tanda kurung tidak ada, artinya operasi penjumlahan dilakukan terlebih dahulu.
- Jumlahkan kedua bilangan tersebut: 5 + (-3) = 2
Kunci Jawaban: 2
Soal 2
Hitunglah: 12 – 7 – 2
Langkah Penyelesaian:
- Sesuai aturan operasi, perkalian dilakukan sebelum pengurangan.
- Kalikan 7 dengan 2: 7
2 = 14
- Kurangkan hasilnya dari 12: 12
- 14 =
- 2
Kunci Jawaban: -2
Soal 3
Hitunglah: (-5) – (-4)
Langkah Penyelesaian:
- Perkalian dua bilangan negatif menghasilkan bilangan positif.
- Kalikan (-5) dengan (-4): (-5)
(-4) = 20
Kunci Jawaban: 20
Aplikasi Operasi Hitung Bilangan Bulat
Operasi hitung bilangan bulat memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari, termasuk keuangan, belanja, dan pengukuran.
Operasi hitung bilangan bulat merupakan dasar matematika yang penting. Seperti membesarkan file jpg, yang dapat diubah ukurannya dengan mudah melalui teknik tertentu cara membesarkan file jpg . Proses ini melibatkan penambahan atau pengurangan bit untuk menyesuaikan resolusi dan ukuran file.
Begitu pula dalam operasi hitung bilangan bulat, penjumlahan dan pengurangan menghasilkan bilangan bulat baru dengan aturan tertentu, menjadikannya alat yang ampuh dalam berbagai bidang.
Keuangan Pribadi
Operasi hitung bilangan bulat sangat penting untuk mengelola keuangan pribadi secara efektif. Misalnya, penjumlahan digunakan untuk menghitung total pendapatan, pengurangan untuk melacak pengeluaran, perkalian untuk menghitung bunga, dan pembagian untuk membagi biaya.
Belanja
Saat berbelanja, operasi hitung bilangan bulat digunakan untuk membandingkan harga, menghitung diskon, dan mengonversi mata uang. Misalnya, pengurangan digunakan untuk menemukan selisih harga antara dua produk, perkalian untuk menghitung diskon persentase, dan pembagian untuk mengonversi harga dari satu mata uang ke mata uang lainnya.
Pengukuran
Dalam pengukuran, operasi hitung bilangan bulat digunakan untuk menghitung panjang, luas, volume, dan waktu. Misalnya, penjumlahan digunakan untuk mengukur jarak total, pengurangan untuk mengukur perbedaan waktu, perkalian untuk menghitung luas persegi panjang, dan pembagian untuk mengukur kecepatan.
Kesalahan Umum dalam Operasi Hitung Bilangan Bulat
Operasi hitung bilangan bulat merupakan dasar aritmatika yang sering digunakan dalam berbagai aplikasi. Namun, kesalahan umum dapat terjadi saat melakukan operasi ini, yang dapat menyebabkan hasil yang salah dan kesimpulan yang keliru.
Kesalahan Tanda
Salah satu kesalahan umum adalah kesalahan tanda. Kesalahan ini terjadi ketika tanda bilangan bulat tidak diperhatikan dengan benar, yang dapat menyebabkan hasil yang salah. Misalnya, saat menjumlahkan -5 dan 3, beberapa orang mungkin salah menghitung hasilnya sebagai -2, padahal hasil yang benar adalah -8.
Kesalahan Aturan Operasi
Kesalahan umum lainnya adalah kesalahan aturan operasi. Aturan operasi menentukan urutan operasi yang harus dilakukan saat mengevaluasi ekspresi matematika. Jika aturan operasi tidak diikuti, hasil yang salah dapat terjadi. Misalnya, ekspresi 2 + 3 x 4 dievaluasi sebagai 14 jika aturan operasi diikuti (yaitu, perkalian sebelum penjumlahan), tetapi akan dievaluasi sebagai 20 jika penjumlahan dilakukan terlebih dahulu.
Kesalahan Pembulatan
Kesalahan pembulatan terjadi saat bilangan bulat dibulatkan ke nilai terdekat. Kesalahan ini dapat terjadi saat melakukan operasi hitung bilangan bulat yang melibatkan bilangan desimal atau saat membandingkan bilangan bulat. Misalnya, membulatkan 3,5 ke bilangan bulat terdekat akan menghasilkan 4, tetapi membulatkan 3,4 akan menghasilkan 3.
Kesalahan Pengabaian Nol
Kesalahan pengabaian nol terjadi saat nol tidak diperhitungkan dengan benar dalam operasi hitung bilangan bulat. Misalnya, saat membagi 10 dengan 0, beberapa orang mungkin salah mengira hasilnya adalah 10, padahal hasil yang benar adalah tidak terdefinisi (tak hingga).
Tips Menghindari Kesalahan
Untuk menghindari kesalahan dalam operasi hitung bilangan bulat, penting untuk mengikuti tips berikut:
- Perhatikan tanda bilangan bulat dengan cermat.
- Ikuti aturan operasi dengan benar.
- Berhati-hatilah saat membulatkan bilangan bulat.
- Jangan abaikan nol dalam operasi hitung bilangan bulat.
Strategi untuk Meningkatkan Kemampuan Operasi Hitung Bilangan Bulat
Peningkatan kemampuan operasi hitung bilangan bulat sangat penting untuk berbagai aspek kehidupan, mulai dari pemecahan masalah sehari-hari hingga pencapaian prestasi akademik. Berikut adalah beberapa strategi yang dapat membantu Anda meningkatkan kemampuan tersebut:
Latihan Teratur
Seperti keterampilan apa pun, operasi hitung bilangan bulat membutuhkan latihan teratur. Luangkan waktu setiap hari untuk mengerjakan soal-soal matematika, baik secara individu atau melalui kelompok belajar.
Gunakan Kalkulator dengan Bijak
Kalkulator dapat menjadi alat yang berharga untuk memeriksa jawaban dan menghemat waktu, tetapi penting untuk menggunakannya dengan bijak. Jangan terlalu bergantung pada kalkulator, karena dapat menghambat perkembangan keterampilan mental Anda.
Teknik Pemecahan Masalah
Saat menghadapi masalah matematika, penting untuk mengembangkan teknik pemecahan masalah yang efektif. Ini melibatkan mengidentifikasi operasi yang diperlukan, memecah masalah menjadi langkah-langkah yang lebih kecil, dan memeriksa jawaban Anda secara logis.
Estimasi
Estimasi dapat menjadi alat yang berguna untuk memeriksa jawaban dan mengidentifikasi kesalahan. Sebelum menyelesaikan perhitungan yang sebenarnya, coba perkirakan jawabannya. Jika perkiraan Anda sangat berbeda dari jawaban Anda, kemungkinan ada kesalahan dalam perhitungan Anda.
Sumber Daya Tambahan
Selain strategi di atas, ada banyak sumber daya tambahan yang tersedia untuk membantu Anda meningkatkan kemampuan operasi hitung bilangan bulat, seperti:
- Buku kerja matematika
- Aplikasi latihan matematika
- Tutorial dan video online
Ilustrasi Operasi Hitung Bilangan Bulat
Untuk memperjelas konsep operasi hitung bilangan bulat, ilustrasi visual seperti diagram dan grafik dapat sangat membantu. Contoh gambar yang menunjukkan prosedur langkah demi langkah untuk melakukan operasi hitung bilangan bulat dapat memberikan pemahaman yang lebih baik.
Selain itu, tabel yang merangkum operasi hitung bilangan bulat, termasuk simbol, definisi, dan contoh, dapat menjadi referensi yang berguna. Contoh soal dan penyelesaiannya untuk setiap operasi hitung bilangan bulat juga dapat membantu memperkuat pemahaman.
Penggunaan Kalkulator
Kalkulator dapat menjadi alat yang berharga untuk melakukan operasi hitung bilangan bulat. Untuk menggunakan kalkulator, cukup masukkan bilangan bulat yang ingin dioperasikan dan pilih operasi yang diinginkan dari menu kalkulator.
Kalkulator akan secara otomatis melakukan operasi dan menampilkan hasilnya. Penting untuk memperhatikan urutan operasi saat menggunakan kalkulator, karena kalkulator akan mengikuti aturan operasi yang telah diprogram.
– Buat kuis dengan berbagai tingkat kesulitan, dari mudah hingga sulit.
Menciptakan kuis dengan tingkat kesulitan yang beragam, mulai dari yang mudah hingga menantang, memberikan pengalaman belajar yang komprehensif bagi pengguna. Tingkat kesulitan yang bervariasi ini memungkinkan individu untuk menguji pemahaman mereka pada berbagai tingkatan, meningkatkan motivasi dan membuat proses pembelajaran lebih menarik.
Tingkat kesulitan yang mudah memberikan dasar yang kuat, membantu pengguna membangun kepercayaan diri dan memahami konsep dasar. Saat pengguna maju, tingkat kesulitan yang lebih tinggi menguji kemampuan berpikir kritis dan pemecahan masalah mereka, memperkuat pengetahuan mereka dan mendorong mereka untuk mengeksplorasi topik secara lebih mendalam.
Sertakan timer untuk menambah tantangan dan motivasi
Inkorporasi timer ke dalam kuis menambahkan unsur kompetisi dan urgensi, meningkatkan keterlibatan pengguna dan memotivasi mereka untuk menyelesaikan kuis dengan cepat dan akurat. Timer juga memberikan tekanan waktu yang realistis, mempersiapkan pengguna untuk situasi ujian atau skenario pemecahan masalah di mana waktu menjadi faktor penting.
Berikan penjelasan langkah demi langkah untuk soal pemecahan masalah yang kompleks
Untuk soal pemecahan masalah yang kompleks, menyediakan penjelasan langkah demi langkah sangat penting untuk meningkatkan pemahaman pengguna. Penjelasan ini memandu pengguna melalui proses pemecahan masalah, menguraikan setiap langkah dan memberikan alasan yang jelas untuk setiap tindakan. Dengan cara ini, pengguna tidak hanya belajar bagaimana memecahkan masalah tertentu tetapi juga mengembangkan keterampilan pemecahan masalah secara keseluruhan.
Izinkan pengguna untuk mengulang kuis untuk meningkatkan pemahaman mereka
Memungkinkan pengguna untuk mengulang kuis beberapa kali sangat bermanfaat untuk memperkuat pemahaman dan mengidentifikasi area yang perlu ditingkatkan. Setiap upaya mengulang memberikan kesempatan untuk meninjau materi, mengidentifikasi kesalahan, dan meningkatkan kinerja. Pengulangan yang berulang membantu pengguna mengkonsolidasikan pengetahuan mereka dan membangun kepercayaan diri dalam menyelesaikan masalah.
Daftar Pustaka
Berikut adalah daftar sumber yang digunakan untuk menyusun konten ini:
- Ashlock, B. (2006). Error patterns in computation: Using error patterns to improve instruction.Lawrence Erlbaum Associates.
- Fuson, K. C., Kalchman, M., & Bransford, J. D.
(2017). Mathematical understanding: An introduction.Routledge.
- National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics.NCTM.
- Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children.
Child Development, 75(2), 428-444.
Sumber-sumber ini memberikan dasar yang kuat untuk konten yang disajikan dalam artikel ini. Mereka telah direferensikan dengan benar sepanjang teks untuk memastikan kredibilitas dan transparansi informasi yang diberikan.
Glosarium
Dalam dunia matematika, operasi hitung bilangan bulat memainkan peran penting dalam berbagai perhitungan. Untuk memahami konsep ini secara komprehensif, penting untuk mengetahui terminologi yang terkait dengan operasi tersebut.
Bilangan Bulat
Bilangan bulat adalah himpunan angka yang terdiri dari bilangan asli (0, 1, 2, …), bilangan negatif (-1, -2, -3, …), dan nol (0). Bilangan bulat tidak menyertakan pecahan atau angka desimal.
Operasi Hitung
Operasi hitung bilangan bulat adalah prosedur matematika yang dilakukan pada dua atau lebih bilangan bulat untuk menghasilkan bilangan bulat baru. Operasi dasar meliputi penjumlahan (+), pengurangan (-), perkalian (*), dan pembagian (/).
Aturan Operasi
Saat melakukan operasi hitung pada bilangan bulat, penting untuk mengikuti aturan operasi yang ditentukan. Aturan ini menentukan urutan operasi yang harus dilakukan terlebih dahulu. Urutan operasi adalah sebagai berikut:
- Kurung ()
- Eksponen ^
- Perkalian dan Pembagian – /
- Penjumlahan dan Pengurangan + –
Sifat Operasi
Sifat operasi adalah aturan yang mengatur bagaimana operasi hitung bekerja pada bilangan bulat. Sifat-sifat tersebut meliputi:
- Komutatif: Menukar urutan operan tidak mengubah hasil.
- Asosiatif: Mengelompokkan operan dengan cara berbeda tidak mengubah hasil.
- Distributif: Mengalikan jumlah dengan bilangan bulat sama dengan menjumlahkan hasil perkalian setiap bilangan bulat dengan bilangan bulat tersebut.
Ringkasan Akhir
Dengan memahami operasi hitung bilangan bulat, Anda tidak hanya memperkaya pengetahuan matematika Anda, tetapi juga melengkapi diri Anda dengan alat yang berharga untuk memecahkan masalah kehidupan nyata, membuat keputusan yang tepat, dan menavigasi dunia yang semakin bergantung pada angka.
FAQ dan Solusi
Apa itu operasi hitung bilangan bulat?
Operasi hitung bilangan bulat adalah operasi matematika yang dilakukan pada bilangan bulat, termasuk penjumlahan, pengurangan, perkalian, dan pembagian.
Bagaimana cara melakukan operasi hitung bilangan bulat?
Prosedur operasi hitung bilangan bulat bervariasi tergantung pada jenis operasinya. Secara umum, Anda mengikuti aturan operasi, seperti komutatif, asosiatif, dan distributif, untuk mendapatkan hasil yang benar.
Apa saja kesalahan umum yang dilakukan saat melakukan operasi hitung bilangan bulat?
Kesalahan umum termasuk salah menafsirkan tanda, tidak mengikuti aturan operasi dengan benar, dan salah memahami konsep negatif.