Dalam matematika, operasi hitung bilangan bulat memegang peran penting dalam berbagai aspek kehidupan. Dari menghitung uang hingga mengukur jarak, pemahaman tentang operasi dasar ini sangatlah penting. Artikel ini akan menyajikan panduan komprehensif tentang cara operasi hitung bilangan bulat, lengkap dengan contoh dan penjelasan langkah demi langkah.
Bilangan bulat adalah himpunan angka yang terdiri dari bilangan asli, nol, dan bilangan negatif. Operasi hitung bilangan bulat meliputi penjumlahan, pengurangan, perkalian, pembagian, dan operasi lainnya yang lebih kompleks.
Operasi Hitung Bilangan Bulat Dasar
Bilangan bulat adalah sekumpulan angka yang terdiri dari bilangan positif, negatif, dan nol. Operasi hitung dasar yang dapat dilakukan pada bilangan bulat adalah penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan
Penjumlahan adalah operasi yang menggabungkan dua bilangan bulat untuk menghasilkan bilangan bulat baru. Penjumlahan dilambangkan dengan tanda “+”. Sifat komutatif penjumlahan menyatakan bahwa mengubah urutan bilangan yang dijumlahkan tidak mengubah hasil penjumlahan.
Pengurangan
Pengurangan adalah operasi yang mengurangi satu bilangan bulat dari bilangan bulat lainnya. Pengurangan dilambangkan dengan tanda “-“. Sifat asosiatif pengurangan menyatakan bahwa mengelompokkan bilangan bulat dalam urutan yang berbeda tidak mengubah hasil pengurangan.
Perkalian
Perkalian adalah operasi yang mengulangi penambahan bilangan bulat yang sama sebanyak kali yang ditentukan. Perkalian dilambangkan dengan tanda “×” atau “.”. Sifat distributif perkalian menyatakan bahwa perkalian suatu bilangan bulat dengan jumlah dua bilangan bulat sama dengan jumlah perkalian bilangan bulat itu dengan masing-masing bilangan bulat.
Pembagian
Pembagian adalah operasi yang mendistribusikan suatu bilangan bulat secara merata ke bilangan bulat lainnya. Pembagian dilambangkan dengan tanda “÷” atau “:”. Pembagian tidak selalu menghasilkan bilangan bulat, dan hasilnya dapat berupa pecahan atau desimal.
Penjumlahan dan Pengurangan Bilangan Bulat
Bilangan bulat adalah bilangan yang dapat ditulis sebagai kelipatan bilangan bulat 1, yang mencakup bilangan positif, nol, dan bilangan negatif. Operasi hitung pada bilangan bulat mengikuti aturan khusus yang membantu kita memahami perilaku bilangan ini.
Penjumlahan bilangan bulat menggabungkan nilai dari dua bilangan atau lebih, sedangkan pengurangan bilangan bulat menunjukkan selisih antara dua bilangan. Dalam kedua operasi ini, tanda bilangan (positif atau negatif) memainkan peran penting dalam menentukan hasil operasi.
Dalam operasi hitung bilangan bulat, penjumlahan dua bilangan positif akan menghasilkan bilangan positif, sedangkan penjumlahan dua bilangan negatif akan menghasilkan bilangan negatif. Menariknya, ketika kita beralih ke ranah finansial, kita dapat menerapkan prinsip yang sama. Jika kita ingin mengajukan cara kredit motor di bank bri , kita perlu memahami operasi penjumlahan pendapatan dan pengeluaran.
Dengan menghitung selisih antara pendapatan dan pengeluaran, kita dapat menentukan kemampuan finansial kita untuk membayar cicilan kredit.
Penjumlahan Bilangan Bulat
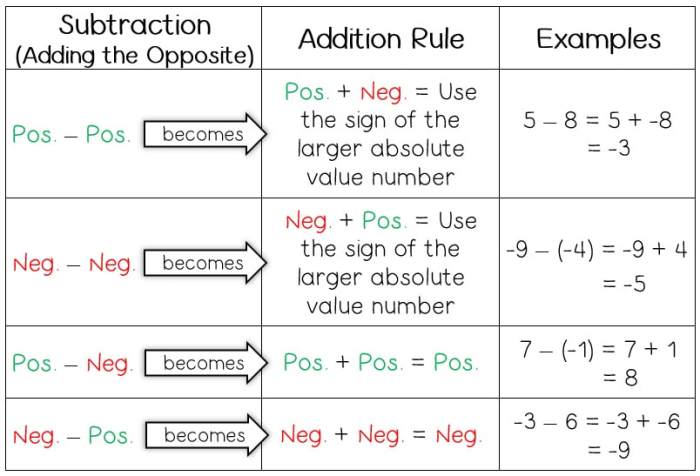
Saat menjumlahkan dua bilangan bulat dengan tanda yang sama (keduanya positif atau negatif), tanda hasilnya akan sama dengan tanda bilangan yang dijumlahkan. Nilai absolut (besarnya) hasil penjumlahan sama dengan jumlah nilai absolut bilangan yang dijumlahkan.
- Jika kedua bilangan positif, jumlahnya positif.
- Jika kedua bilangan negatif, jumlahnya negatif.
Pengurangan Bilangan Bulat
Saat mengurangi dua bilangan bulat dengan tanda yang sama, tanda hasilnya akan berlawanan dengan tanda bilangan yang dikurangi. Nilai absolut hasil pengurangan sama dengan selisih nilai absolut bilangan yang dikurangi.
Operasi hitung bilangan bulat merupakan dasar matematika yang penting. Namun, tahukah Anda bahwa prinsip serupa juga berlaku dalam memasak? Sama seperti menggabungkan bilangan, memasak gandum utuh membutuhkan langkah-langkah berurutan, seperti membersihkan, merendam, dan memasak . Proses ini menggabungkan bahan-bahan dasar untuk menghasilkan hidangan yang lezat.
Dengan memahami cara mengoperasikan bilangan bulat, Anda juga dapat menguasai seni memasak gandum utuh yang sempurna.
- Jika kedua bilangan positif, selisihnya positif.
- Jika kedua bilangan negatif, selisihnya negatif.
Tanda Berbeda dalam Penjumlahan dan Pengurangan
Ketika menjumlahkan atau mengurangi bilangan bulat dengan tanda yang berbeda, aturannya sedikit berbeda:
- Penjumlahan:Jika satu bilangan positif dan satu bilangan negatif, tanda hasilnya akan sama dengan tanda bilangan dengan nilai absolut lebih besar.
- Pengurangan:Jika satu bilangan positif dan satu bilangan negatif, tanda hasilnya akan sama dengan tanda bilangan yang dikurangi (yang ditulis di depan).
Aturan-aturan ini memungkinkan kita untuk melakukan operasi hitung pada bilangan bulat secara akurat, bahkan ketika tanda-tanda bilangan tersebut berbeda.
Perkalian dan Pembagian Bilangan Bulat
Operasi perkalian dan pembagian bilangan bulat mengikuti aturan yang jelas untuk menentukan tanda hasil operasi. Aturan ini didasarkan pada prinsip matematika yang telah terbukti dan memberikan dasar untuk operasi aritmatika dasar.
Langkah-langkah Perkalian Bilangan Bulat
- Kalikan kedua bilangan tersebut tanpa memperhatikan tanda.
- Jika kedua bilangan memiliki tanda yang sama (positif atau negatif), hasil operasi adalah positif.
- Jika kedua bilangan memiliki tanda yang berbeda (satu positif dan satu negatif), hasil operasi adalah negatif.
Langkah-langkah Pembagian Bilangan Bulat
- Bagilah bilangan yang lebih besar (pembilang) dengan bilangan yang lebih kecil (penyebut) tanpa memperhatikan tanda.
- Jika pembilang dan penyebut memiliki tanda yang sama (positif atau negatif), hasil operasi adalah positif.
- Jika pembilang dan penyebut memiliki tanda yang berbeda (satu positif dan satu negatif), hasil operasi adalah negatif.
Tabel Aturan Perkalian dan Pembagian Bilangan Bulat
| Operasi | Tanda Bilangan | Hasil Tanda |
|---|---|---|
| Perkalian | Sama | Positif |
| Perkalian | Berbeda | Negatif |
| Pembagian | Sama | Positif |
| Pembagian | Berbeda | Negatif |
Contoh
- 5 x (-3) = -15 (tanda berbeda, hasil negatif)
- (-4) x (-6) = 24 (tanda sama, hasil positif)
- 12 ÷ (-4) = -3 (pembilang dan penyebut tanda berbeda, hasil negatif)
- (-15) ÷ 3 = -5 (pembilang dan penyebut tanda sama, hasil positif)
Berikan contoh soal hitung bilangan bulat yang melibatkan operasi dengan prioritas yang berbeda dan jelaskan langkah-langkah penyelesaiannya.
Pertimbangkan soal berikut: 10 – 5 x (2 + 3) x 4
Urutan operasi prioritas, dari yang tertinggi hingga terendah, adalah:
- Tanda kurung
- Eksponen
- Perkalian dan Pembagian
- Penjumlahan dan Pengurangan
Langkah penyelesaian:
- Hitung operasi dalam tanda kurung terlebih dahulu: 2 + 3 = 5
- Lakukan perkalian: 5 x 5 = 25
- Lakukan perkalian lagi: 25 x 4 = 100
- Terakhir, lakukan pengurangan: 10
- 100 =
- 90
Jadi, hasil dari soal tersebut adalah -90.
Bilangan Campuran dan Bilangan Desimal
Bilangan campuran adalah bilangan yang terdiri dari bagian bilangan bulat dan bagian pecahan. Bilangan desimal adalah bilangan yang dinyatakan menggunakan angka di belakang titik desimal.
Mengubah Bilangan Campuran menjadi Bilangan Desimal
Untuk mengubah bilangan campuran menjadi bilangan desimal, ikuti langkah-langkah berikut:
- Kalikan bagian bilangan bulat dengan penyebut pecahan.
- Tambahkan hasil perkalian dengan pembilang pecahan.
- Bagi hasil penjumlahan dengan penyebut pecahan.
Contoh:
Mengubah 2 1/4 menjadi desimal:
- 2 x 4 = 8
- 8 + 1 = 9
- 9 / 4 = 2,25
Mengubah Bilangan Desimal menjadi Bilangan Campuran, Cara operasi hitung bilangan bulat
Untuk mengubah bilangan desimal menjadi bilangan campuran, ikuti langkah-langkah berikut:
- Ambil bagian bilangan bulat dari bilangan desimal.
- Kalikan bagian desimal dengan penyebut pecahan yang diinginkan.
- Ambil bagian bilangan bulat dari hasil perkalian sebagai pembilang pecahan.
- Penyebut pecahan adalah penyebut yang dipilih pada langkah 2.
Contoh:
Mengubah 2,25 menjadi bilangan campuran:
- Bagian bilangan bulat: 2
- Bagian desimal: 0,25
- 0,25 x 100 = 25
- Pembilang pecahan: 25
- Penyebut pecahan: 100
- Bilangan campuran: 2 25/100
– Jelaskan konsep persamaan bilangan bulat.
Persamaan bilangan bulat adalah persamaan matematika yang melibatkan bilangan bulat, yaitu bilangan yang tidak mengandung bagian desimal atau pecahan. Persamaan bilangan bulat digunakan untuk mewakili berbagai situasi di dunia nyata, seperti mencari jumlah atau perbedaan antara bilangan.
Langkah-langkah menyelesaikan persamaan bilangan bulat sederhana.
- Hapus tanda kurung dengan mengalikan kedua sisi persamaan dengan angka di dalam kurung.
- Gabungkan suku-suku serupa pada setiap sisi persamaan.
- Pindahkan suku yang mengandung variabel ke satu sisi persamaan dan suku yang tidak mengandung variabel ke sisi lainnya.
- Bagi kedua sisi persamaan dengan koefisien variabel untuk menyelesaikan variabel.
Cara menyelesaikan persamaan bilangan bulat dengan variabel pada kedua sisi.
Ketika persamaan bilangan bulat memiliki variabel pada kedua sisi, pertama-tama pindahkan semua suku yang mengandung variabel ke satu sisi persamaan dan suku yang tidak mengandung variabel ke sisi lainnya. Kemudian, gabungkan suku-suku serupa dan bagi kedua sisi persamaan dengan koefisien variabel untuk menyelesaikan variabel.
Contoh persamaan bilangan bulat dan cara menyelesaikannya langkah demi langkah.
Misalkan kita memiliki persamaan 2x + 5 = 11. Untuk menyelesaikan persamaan ini, kita dapat mengikuti langkah-langkah berikut:
- Hapus tanda kurung dengan mengalikan kedua sisi persamaan dengan 1.
- Gabungkan suku-suku serupa: 2x + 5 = 11
- Pindahkan suku yang mengandung variabel ke satu sisi persamaan dan suku yang tidak mengandung variabel ke sisi lainnya: 2x = 6
- Bagi kedua sisi persamaan dengan koefisien variabel: x = 3
Jadi, solusi untuk persamaan 2x + 5 = 11 adalah x = 3.
Pertidaksamaan Bilangan Bulat
Pertidaksamaan bilangan bulat adalah perbandingan dua bilangan bulat yang menunjukkan apakah salah satu bilangan lebih besar, lebih kecil, atau sama dengan yang lain.
Simbol yang digunakan dalam pertidaksamaan bilangan bulat adalah:
- >: lebih besar dari
- <: lebih kecil dari
- ≥: lebih besar dari atau sama dengan
- ≤: lebih kecil dari atau sama dengan
Langkah-Langkah Menyelesaikan Pertidaksamaan Bilangan Bulat
Untuk menyelesaikan pertidaksamaan bilangan bulat, ikuti langkah-langkah berikut:
- Tentukan apakah kedua sisi pertidaksamaan adalah bilangan positif atau negatif.
- Jika kedua sisi positif, kalikan atau bagi kedua sisi dengan bilangan negatif untuk membalik tanda pertidaksamaan.
- Jika kedua sisi negatif, kalikan atau bagi kedua sisi dengan bilangan negatif untuk membalik tanda pertidaksamaan.
- Jika satu sisi positif dan sisi lainnya negatif, tidak ada solusi.
Contoh
Selesaikan pertidaksamaan berikut:
3 >
5
Kedua sisi positif, jadi kita dapat membagi kedua sisi dengan 3:
3 / 3 >
5 / 3
1 >
1,67
Jadi, pertidaksamaan ini memiliki solusi.
Aplikasi Operasi Bilangan Bulat dalam Kehidupan Sehari-hari
Operasi bilangan bulat memainkan peran penting dalam kehidupan sehari-hari kita, memungkinkan kita melakukan berbagai tugas dengan mudah dan akurat. Dari menghitung uang hingga mengukur jarak dan menghitung waktu, operasi bilangan bulat sangat penting untuk memahami dunia di sekitar kita.
Menghitung Uang
Salah satu aplikasi paling umum dari operasi bilangan bulat adalah menghitung uang. Ketika kita membeli sesuatu, kita perlu menambahkan harga barang untuk menentukan totalnya. Ketika kita menerima uang kembali, kita perlu mengurangi jumlah uang yang kita bayarkan dari jumlah uang yang kita terima untuk menentukan kembalian kita.
Mengukur Jarak
Operasi bilangan bulat juga digunakan untuk mengukur jarak. Ketika kita mengemudi, kita perlu menghitung jarak yang kita tempuh untuk mengetahui seberapa jauh kita telah melakukan perjalanan. Kita juga perlu menghitung jarak antara dua titik untuk menentukan rute terpendek atau tercepat.
Menghitung Waktu
Operasi bilangan bulat juga digunakan untuk menghitung waktu. Ketika kita merencanakan perjalanan, kita perlu menambahkan waktu yang dibutuhkan untuk sampai ke tujuan kita untuk menentukan waktu kedatangan kita. Kita juga perlu mengurangi waktu mulai dari waktu berakhir untuk menentukan durasi suatu peristiwa.
Sifat-sifat Bilangan Bulat
Bilangan bulat adalah himpunan angka yang terdiri dari bilangan asli (1, 2, 3, …), bilangan nol (0), dan kebalikan dari bilangan asli (…, -3, -2, -1).
Sifat Tertutup
Operasi hitung bilangan bulat, yaitu penjumlahan, pengurangan, perkalian, dan pembagian (dengan pembagi bukan nol), selalu menghasilkan bilangan bulat.
Sifat Terurut
Bilangan bulat dapat disusun dalam urutan dari yang terkecil hingga terbesar. Urutan ini disebut garis bilangan.
Sifat Nol
- Penjumlahan bilangan bulat sembarang dengan nol sama dengan bilangan bulat itu sendiri.
- Perkalian bilangan bulat sembarang dengan nol menghasilkan nol.
Sifat Invers
Setiap bilangan bulat memiliki kebalikannya, yang jika dijumlahkan akan menghasilkan nol.
| Sifat | Deskripsi |
|---|---|
| Tertutup | Operasi hitung menghasilkan bilangan bulat. |
| Terurut | Bilangan bulat dapat disusun dalam urutan. |
| Sifat Nol | Penjumlahan/perkalian dengan nol menghasilkan bilangan/nol. |
| Sifat Invers | Setiap bilangan bulat memiliki kebalikannya. |
Memahami sifat-sifat bilangan bulat sangat penting dalam operasi hitung karena memungkinkan kita untuk melakukan perhitungan dengan benar dan memahami hubungan antar bilangan bulat.
“Memahami sifat-sifat bilangan bulat adalah dasar untuk membangun pemahaman yang kuat tentang matematika.”- Dr. Maria A. Rivera, Profesor Matematika
Sifat-sifat bilangan bulat dapat dianalogikan dengan sistem penomoran. Setiap digit mewakili bilangan bulat, dan aturan operasi hitung mengikuti sifat-sifat bilangan bulat, memungkinkan kita untuk melakukan perhitungan kompleks dengan mudah dan akurat.
Representasi Grafik Bilangan Bulat: Cara Operasi Hitung Bilangan Bulat
Garis bilangan adalah representasi grafis bilangan bulat yang sangat berguna. Garis ini memiliki titik nol (0) di tengahnya, dengan bilangan bulat positif di sebelah kanan dan bilangan bulat negatif di sebelah kiri.
Setiap titik pada garis bilangan mewakili satu bilangan bulat. Jarak antara dua titik yang berdekatan adalah 1. Bilangan bulat positif semakin besar semakin jauh jaraknya dari nol ke kanan, sedangkan bilangan bulat negatif semakin kecil semakin jauh jaraknya dari nol ke kiri.
Dalam operasi hitung bilangan bulat, penjumlahan dan pengurangan mengikuti aturan yang sama seperti operasi aritmatika biasa. Namun, perkalian dan pembagian memiliki aturan khusus untuk bilangan positif dan negatif. Menariknya, prinsip ini juga berlaku saat kita mengatur printer untuk mencetak bolak-balik ( cara setting print bolak balik ). Sama seperti bilangan bulat, printer membutuhkan pengaturan khusus untuk mencetak halaman ganjil dan genap pada sisi yang berlawanan.
Dengan memahami prinsip operasi hitung bilangan bulat dan pengaturan printer bolak-balik, kita dapat memastikan hasil yang akurat dan efisien baik dalam perhitungan matematika maupun pencetakan dokumen.
Menjumlahkan dan Mengurangi Bilangan Bulat
Untuk menjumlahkan dua bilangan bulat pada garis bilangan, mulailah dari bilangan bulat pertama dan gerakkan ke kanan sebanyak bilangan bulat kedua. Bilangan bulat yang Anda dapatkan adalah hasil penjumlahannya.
Untuk mengurangi bilangan bulat, mulailah dari bilangan bulat pertama dan gerakkan ke kiri sebanyak bilangan bulat kedua. Bilangan bulat yang Anda dapatkan adalah hasil pengurangannya.
Membandingkan Bilangan Bulat
Untuk membandingkan dua bilangan bulat, lihat posisi mereka pada garis bilangan. Bilangan bulat yang lebih jauh ke kanan lebih besar, sedangkan bilangan bulat yang lebih jauh ke kiri lebih kecil.
Menggunakan Garis Bilangan untuk Operasi Hitung
Garis bilangan dapat digunakan untuk melakukan berbagai operasi hitung, termasuk penjumlahan, pengurangan, perkalian, dan pembagian. Metode ini sangat berguna untuk bilangan bulat kecil atau saat tidak ada kalkulator yang tersedia.
Berikut adalah contoh soal yang dapat diselesaikan menggunakan garis bilangan:
+ (-5) = ?
Mulai dari 3 pada garis bilangan dan gerakkan ke kiri 5 satuan. Hasilnya adalah -2, yang merupakan jawabannya.
Bilangan Genap dan Ganjil
Bilangan genap dan ganjil adalah dua kategori dasar dalam matematika. Konsep ini sangat penting dalam berbagai bidang, termasuk aljabar, analisis, dan ilmu komputer.
Bilangan Genap
Bilangan genap adalah bilangan bulat yang habis dibagi 2. Dengan kata lain, bilangan genap adalah bilangan yang dapat dinyatakan sebagai 2n, di mana n adalah bilangan bulat apa pun. Misalnya, -4, 0, 8, dan 100 adalah bilangan genap.
Bilangan Ganjil
Bilangan ganjil adalah bilangan bulat yang tidak habis dibagi 2. Dengan kata lain, bilangan ganjil adalah bilangan yang dapat dinyatakan sebagai 2n + 1, di mana n adalah bilangan bulat apa pun. Misalnya, -3, 1, 7, dan 99 adalah bilangan ganjil.
Sifat Bilangan Genap dan Ganjil
Bilangan genap dan ganjil memiliki beberapa sifat yang berbeda:
- Jumlah dua bilangan genap adalah genap.
- Jumlah dua bilangan ganjil adalah genap.
- Jumlah bilangan genap dan ganjil adalah ganjil.
- Perkalian dua bilangan genap adalah genap.
- Perkalian dua bilangan ganjil adalah ganjil.
- Perkalian bilangan genap dan ganjil adalah genap.
– Jelaskan konsep faktor dan kelipatan bilangan bulat.
Dalam matematika, faktor adalah bilangan yang dapat membagi bilangan lain secara habis, sedangkan kelipatan adalah bilangan yang merupakan hasil perkalian bilangan lain. Bilangan bulat adalah bilangan yang tidak memiliki bagian desimal, seperti -3, 0, dan 7.
Langkah-langkah Mencari Faktor dan Kelipatan
- Untuk mencari faktor suatu bilangan bulat, bagi bilangan tersebut dengan bilangan bulat positif yang lebih kecil dari bilangan itu.
- Untuk mencari kelipatan suatu bilangan bulat, kalikan bilangan tersebut dengan bilangan bulat positif.
Hubungan antara Faktor dan Kelipatan
Faktor dan kelipatan memiliki hubungan yang erat. Setiap faktor suatu bilangan juga merupakan kelipatan dari dirinya sendiri. Sebaliknya, setiap kelipatan suatu bilangan juga merupakan faktor dari bilangan itu sendiri.
Contoh Faktor dan Kelipatan
Faktor-faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12.
Kelipatan dari 5 adalah 5, 10, 15, 20, 25, dan seterusnya.
Program untuk Menemukan Faktor dan Kelipatan
Berikut adalah program Python sederhana untuk menemukan faktor dan kelipatan suatu bilangan bulat:
def faktor(n): """Menemukan faktor-faktor suatu bilangan bulat n.""" faktor = [] for i in range(1, n + 1): if n % i == 0: faktor.append(i) return faktordef kelipatan(n): """Menemukan kelipatan-kelipatan suatu bilangan bulat n.""" kelipatan = [] i = 1 while i
n <= 100
kelipatan.append(i - n) i += 1 return kelipatan
if __name__ == "__main__": n = int(input("Masukkan bilangan bulat: ")) print("Faktor-faktor dari", n, "adalah", faktor(n)) print("Kelipatan-kelipatan dari", n, "adalah", kelipatan(n))
Pembagian Bersisa
Pembagian bersisa adalah operasi matematika yang membagi suatu bilangan (pembagi) dengan bilangan lain (pembagi) dan menghasilkan dua bilangan: hasil bagi dan sisa. Sisa adalah bilangan yang tidak dapat dibagi habis oleh pembagi.
Pembagian bersisa digunakan dalam berbagai bidang, seperti matematika, ilmu komputer, dan teori bilangan. Dalam matematika, pembagian bersisa digunakan untuk menentukan apakah suatu bilangan habis dibagi oleh bilangan lain, untuk menemukan faktor-faktor suatu bilangan, dan untuk menyelesaikan masalah-masalah lain.
Metode Pembagian Bersisa
- Metode Long Division:Metode ini melibatkan pembagian pembagi ke dalam pembagi berulang kali dan mengurangi hasil kali dari hasil bagi dengan pembagi dari pembagi. Proses ini diulangi hingga tidak ada sisa atau sisa lebih kecil dari pembagi.
- Metode Bersusun:Metode ini melibatkan penyusunan pembagi dan pembagi dalam bentuk kolom dan melakukan operasi aritmatika untuk menemukan hasil bagi dan sisa.
Aplikasi Pembagian Bersisa
“Pembagian bersisa banyak digunakan dalam berbagai bidang, seperti matematika, ilmu komputer, dan teori bilangan.”
Pangkat dan Akar Bilangan Bulat
Dalam dunia matematika, pangkat dan akar bilangan bulat memainkan peran penting dalam berbagai operasi dan konsep. Pangkat mewakili perkalian bilangan yang sama berulang kali, sedangkan akar mewakili operasi kebalikan dari pangkat, yaitu menemukan faktor yang dikalikan untuk menghasilkan bilangan tertentu.
Untuk memahami konsep pangkat dan akar, mari kita bahas secara mendalam:
Pangkat Bilangan Bulat
Pangkat bilangan bulat dilambangkan dengan notasi a n, di mana a adalah bilangan dasarnya dan n adalah pangkatnya. Pangkat menunjukkan bahwa bilangan dasar a dikalikan dengan dirinya sendiri n kali. Misalnya, 3 4berarti 3 × 3 × 3 × 3 = 81.
Sifat-sifat Pangkat Bilangan Bulat
- a 1= a
- a 0= 1
- a m× a n= a m+n
- (a m) n= a mn
Akar Bilangan Bulat
Akar bilangan bulat, juga dikenal sebagai akar pangkat n, adalah bilangan yang, ketika dipangkatkan n kali, menghasilkan bilangan asli. Akar bilangan bulat dilambangkan dengan √ na, di mana a adalah bilangan asli dan n adalah indeks akarnya. Misalnya, √ 327 = 3 karena 3 3= 27.
Sifat-sifat Akar Bilangan Bulat
- √ na n= a
- √ m(√ na) = √ mna
- √ n(ab) = √ na × √ nb
Bilangan Prima dan Komposit
Dalam dunia matematika, bilangan dapat diklasifikasikan menjadi dua kategori utama: prima dan komposit. Bilangan prima adalah bilangan bulat positif yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Sementara itu, bilangan komposit adalah bilangan bulat positif yang memiliki lebih dari dua faktor.
Operasi hitung bilangan bulat sangatlah penting dalam matematika, membantu kita memahami dasar-dasar perhitungan. Namun, tahukah Anda bahwa ada cara untuk mengatasi mata minus jauh? Cara mengatasi mata minus jauh ini melibatkan teknik tertentu yang dapat memperkuat otot mata dan meningkatkan penglihatan.
Dengan memahami cara operasi hitung bilangan bulat dan cara mengatasi mata minus jauh, kita dapat memperkaya pengetahuan kita dan menjaga kesehatan mata kita tetap optimal.
Menentukan Bilangan Prima dan Komposit
Untuk menentukan apakah suatu bilangan prima atau komposit, dapat digunakan langkah-langkah berikut:
- Bagi bilangan tersebut dengan semua bilangan bulat positif dari 2 hingga akar kuadrat dari bilangan tersebut.
- Jika bilangan tersebut habis dibagi oleh salah satu bilangan tersebut, maka bilangan tersebut adalah komposit.
- Jika bilangan tersebut tidak habis dibagi oleh bilangan bulat positif mana pun, maka bilangan tersebut adalah prima.
Sifat Bilangan Prima dan Komposit
Bilangan prima dan komposit memiliki sifat yang berbeda, antara lain:
| Sifat | Bilangan Prima | Bilangan Komposit |
|---|---|---|
| Faktor | Hanya memiliki dua faktor (1 dan bilangan itu sendiri) | Memiliki lebih dari dua faktor |
| Kelipatan | Hanya memiliki dua kelipatan (1 dan bilangan itu sendiri) | Memiliki lebih dari dua kelipatan |
| Pembagi | Hanya memiliki dua pembagi (1 dan bilangan itu sendiri) | Memiliki lebih dari dua pembagi |
| Keunikan | Hanya satu bilangan prima dengan nilai tertentu | Ada banyak bilangan komposit dengan nilai tertentu |