Cara mengatasi uji normalitas eviews – Uji normalitas EViews adalah alat penting untuk menentukan apakah data Anda terdistribusi normal. Dengan menggunakan panduan langkah demi langkah ini, Anda dapat dengan mudah melakukan uji normalitas di EViews, menafsirkan hasilnya, dan mengambil tindakan yang sesuai untuk memastikan data Anda memenuhi asumsi normalitas yang diperlukan untuk analisis statistik yang valid.
Dalam artikel ini, kita akan membahas langkah-langkah uji normalitas, jenis-jenis uji yang tersedia, cara menafsirkan hasil, dan strategi untuk mengatasi ketidaknormalan data. Dengan mengikuti langkah-langkah ini, Anda dapat meningkatkan akurasi dan keandalan analisis statistik Anda.
Definisi Uji Normalitas
Uji normalitas adalah prosedur statistik yang digunakan untuk menentukan apakah suatu kumpulan data mengikuti distribusi normal, juga dikenal sebagai distribusi Gaussian.
Tujuan utama uji normalitas adalah untuk mengidentifikasi apakah asumsi normalitas, yang umum dalam banyak metode statistik, terpenuhi.
Contoh data yang memerlukan uji normalitas antara lain data tinggi badan, nilai ujian, dan hasil survei.
Asumsi yang mendasari uji normalitas adalah bahwa data diambil dari populasi yang terdistribusi normal.
Jenis Uji Normalitas
- Uji Shapiro-Wilk
- Uji Kolmogorov-Smirnov
- Uji Anderson-Darling
- Uji Jarque-Bera
Jenis-Jenis Uji Normalitas
Dalam statistik, uji normalitas digunakan untuk menentukan apakah data mengikuti distribusi normal. Terdapat beberapa jenis uji normalitas yang umum digunakan, masing-masing dengan kekuatan dan kelemahannya sendiri.
Uji Shapiro-Wilk
Uji Shapiro-Wilk adalah uji non-parametrik yang mengukur seberapa dekat distribusi data dengan distribusi normal. Uji ini kuat terhadap data yang tidak normal, namun dapat kurang bertenaga untuk sampel kecil.
Uji Jarque-Bera
Uji Jarque-Bera adalah uji parametrik yang mengukur asimetri dan kurtosis data. Uji ini bertenaga untuk sampel besar, namun dapat dipengaruhi oleh pencilan.
Dalam dunia penelitian ekonometrika, uji normalitas menjadi tantangan yang sering dihadapi. Untuk mengatasinya, salah satu cara yang dapat digunakan adalah dengan transformasi data. Sementara itu, di era digital, teknologi seperti cara menggunakan taps for money menjadi solusi praktis untuk transaksi keuangan.
Kembali pada topik uji normalitas, metode transformasi data dapat membantu mendistribusikan data secara normal, sehingga memenuhi asumsi dasar analisis statistik.
Uji Anderson-Darling
Uji Anderson-Darling adalah uji parametrik yang mengukur perbedaan antara distribusi data dan distribusi normal. Uji ini bertenaga untuk sampel besar dan kecil, serta dapat mendeteksi berbagai jenis penyimpangan dari normalitas.
| Uji | Kekuatan | Kelemahan | Asumsi |
|---|---|---|---|
| Shapiro-Wilk | Kuas untuk data non-normal | Kurang bertenaga untuk sampel kecil | Tidak ada |
| Jarque-Bera | Bertenaga untuk sampel besar | Dapat dipengaruhi oleh pencilan | Data normal |
| Anderson-Darling | Bertenaga untuk sampel besar dan kecil | Tidak ada | Data normal |
Pemilihan uji normalitas yang tepat bergantung pada ukuran sampel, jenis data, dan asumsi yang mendasari. Sebagai panduan umum, uji Shapiro-Wilk cocok untuk data non-normal dan sampel kecil, uji Jarque-Bera cocok untuk sampel besar, dan uji Anderson-Darling cocok untuk semua jenis data dan ukuran sampel.
Cara Melakukan Uji Normalitas di EViews: Cara Mengatasi Uji Normalitas Eviews
Uji normalitas digunakan untuk menentukan apakah suatu variabel terdistribusi normal. Ini penting karena banyak metode statistik mengasumsikan bahwa data terdistribusi normal.
Berikut langkah-langkah untuk melakukan uji normalitas di EViews:
Memuat Data
Muat data ke dalam EViews menggunakan menu File > Open.
Memilih Variabel
Pilih variabel yang akan diuji dari Workfile Browser.
Memilih Uji Normalitas
Pilih menu View > Descriptive Statistics > Normality Tests.
Pilih jenis uji normalitas yang diinginkan (misalnya, Shapiro-Wilk, Kolmogorov-Smirnov).
Menafsirkan Hasil
Hasil uji normalitas akan menampilkan nilai p. Jika nilai p kurang dari tingkat signifikansi (misalnya, 0,05), maka data dianggap tidak terdistribusi normal.
Dalam mengolah data statistik, uji normalitas menjadi langkah krusial. EViews menyediakan beberapa metode untuk mengatasinya. Salah satunya dengan transformasi data, seperti log atau akar kuadrat. Namun, bagi pengguna awam, proses ini mungkin terasa rumit. Sebagai alternatif, Anda dapat mencoba cara unik untuk mengalihkan pikiran sejenak, yaitu mempelajari cara memakai topi baret pramuka . Teknik melipat dan membentuk topi yang rapi dapat membantu menenangkan pikiran dan meningkatkan fokus.
Setelah merasa lebih segar, Anda dapat kembali ke tugas mengatasi uji normalitas EViews dengan perspektif baru.
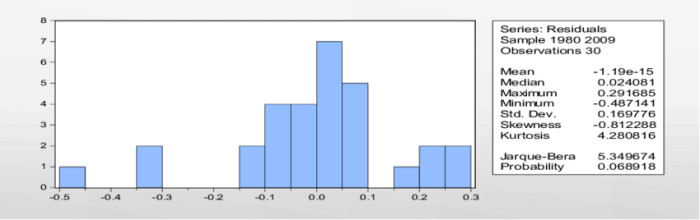
Selain nilai p, EViews juga menampilkan histogram, plot Q-Q, dan statistik deskriptif untuk membantu menafsirkan hasil.
Opsi Dialog
Dialog uji normalitas menyediakan beberapa opsi, termasuk:
- Metode uji: Shapiro-Wilk, Kolmogorov-Smirnov, Jarque-Bera
- Tingkat signifikansi: 0,01, 0,05, 0,10
- Output grafis: Histogram, plot Q-Q, plot P-P
Contoh Kasus
Misalkan kita memiliki data tinggi badan (dalam cm) untuk sekelompok orang dewasa. Kita ingin menguji apakah data tersebut terdistribusi normal.
Untuk mengatasi uji normalitas di EViews, kita dapat menggunakan transformasi data seperti log atau kuadrat. Jika data masih tidak normal, kita dapat mencoba teknik non-parametrik atau melakukan registrasi kartu debit BCA di ATM terdekat. Cara registrasi BCA di ATM cukup mudah, cukup masukkan kartu dan ikuti petunjuk pada layar.
Setelah registrasi berhasil, kita dapat kembali fokus pada analisis data di EViews dan melanjutkan dengan langkah-langkah selanjutnya.
Setelah melakukan uji normalitas, kita mendapatkan nilai p sebesar 0,12. Karena nilai p lebih besar dari 0,05, maka kita gagal menolak hipotesis nol bahwa data terdistribusi normal.
Keterbatasan
Uji normalitas memiliki beberapa keterbatasan, antara lain:
- Uji normalitas hanya menguji apakah data terdistribusi normal atau tidak. Tidak dapat menentukan jenis distribusi non-normal.
- Uji normalitas sensitif terhadap ukuran sampel. Sampel yang lebih besar cenderung menghasilkan nilai p yang lebih kecil, sehingga lebih mungkin menolak hipotesis nol.
Cara Mengatasi Ketidaknormalan Data
Ketidaknormalan data dapat menjadi kendala dalam analisis statistik. Berikut beberapa metode yang dapat digunakan untuk mengatasi data yang tidak normal:
Transformasi Data
Transformasi data melibatkan pengubahan data ke skala yang lebih sesuai. Transformasi umum yang digunakan meliputi:
- Logaritma:Mengubah data menjadi skala logaritmik untuk menormalkan distribusi data yang miring positif.
- Akar Kuadrat:Mengubah data menjadi skala akar kuadrat untuk menormalkan distribusi data yang miring negatif.
Kasus Contoh
Misalkan kita memiliki data waktu yang menunjukkan waktu tunggu pelanggan di bank. Data tersebut miring positif, dengan nilai yang lebih besar pada sisi kanan. Untuk menormalkan data, kita dapat menggunakan transformasi logaritma:
Data Tertransformasi = log(Data Asli)
Setelah transformasi, distribusi data akan lebih normal, memungkinkan kita untuk melanjutkan analisis statistik dengan asumsi normalitas.
Metode Alternatif
Selain transformasi data, terdapat metode alternatif untuk mengatasi ketidaknormalan data, seperti:
- Pemotongan Data:Membuang data yang tidak normal.
- Pengambilan Sampel Ulang Bootstrap:Membuat sampel ulang data untuk mendapatkan distribusi yang lebih normal.
- Metode Non-Parametrik:Menggunakan uji statistik yang tidak bergantung pada asumsi normalitas.
Pemilihan metode yang tepat bergantung pada sifat data dan tujuan analisis.
Dampak Ketidaknormalan Data pada Analisis Statistik
Ketidaknormalan data mengacu pada penyimpangan distribusi data dari distribusi normal. Distribusi normal adalah distribusi simetris berbentuk lonceng yang banyak ditemukan di alam. Ketika data tidak normal, hasil analisis statistik dapat menjadi bias atau tidak akurat.
Konsekuensi Ketidaknormalan Data
Ketidaknormalan data dapat memengaruhi analisis statistik dalam beberapa cara:
- Pengujian Hipotesis:Uji hipotesis mengandalkan distribusi normal untuk menghitung nilai-p. Ketika data tidak normal, nilai-p dapat tidak akurat, sehingga menyebabkan kesimpulan yang salah.
- Estimasi Model:Model statistik yang mengasumsikan distribusi normal dapat menghasilkan estimasi parameter yang bias jika data tidak normal.
- Kekuatan Uji:Kekuatan uji mengacu pada kemampuan untuk mendeteksi perbedaan yang sebenarnya. Ketidaknormalan dapat mengurangi kekuatan uji, sehingga meningkatkan kemungkinan kesalahan Tipe II (gagal mendeteksi perbedaan yang sebenarnya).
Contoh Dampak Ketidaknormalan
Sebagai contoh, pertimbangkan sebuah studi yang menyelidiki perbedaan tinggi badan antara dua kelompok orang. Jika tinggi badan tidak normal, distribusi data akan miring atau kurtosis. Dalam kasus ini, uji-t dua sampel akan menghasilkan nilai-p yang tidak akurat, yang dapat menyebabkan kesimpulan yang salah tentang apakah ada perbedaan tinggi badan yang signifikan antara kedua kelompok.
Cara Mengatasi Ketidaknormalan Data
Ada beberapa cara untuk mengatasi ketidaknormalan data, termasuk:
- Transformasi Data:Transformasi data dapat menormalkan distribusi data dengan mengubah skala atau bentuknya.
- Penggunaan Metode Non-Parametrik:Metode non-parametrik tidak mengasumsikan distribusi normal dan dapat digunakan untuk menganalisis data yang tidak normal.
- Bootstrapping:Bootstrapping adalah teknik resampling yang dapat digunakan untuk menghasilkan distribusi sampling data yang tidak normal.
Memeriksa dan mengatasi ketidaknormalan data sangat penting untuk memastikan hasil analisis statistik yang akurat dan dapat diandalkan.
Pedoman Umum untuk Uji Normalitas
Uji normalitas merupakan metode statistik yang digunakan untuk menentukan apakah data mengikuti distribusi normal. Distribusi normal, juga dikenal sebagai distribusi Gaussian atau distribusi lonceng, adalah distribusi probabilitas yang umum digunakan dalam statistik. Data yang terdistribusi normal memiliki karakteristik tertentu, seperti simetri di sekitar nilai rata-rata dan kemiringan yang khas.
Uji normalitas penting untuk mengidentifikasi penyimpangan dari distribusi normal, yang dapat memengaruhi hasil analisis statistik.
Asumsi yang mendasari uji normalitas adalah bahwa data berasal dari populasi yang terdistribusi normal. Jika asumsi ini tidak terpenuhi, uji normalitas dapat memberikan hasil yang tidak akurat. Terdapat beberapa keterbatasan uji normalitas, seperti sensitivitas terhadap ukuran sampel dan kecenderungan untuk menolak normalitas ketika data mendekati distribusi normal.
Uji normalitas harus digunakan ketika peneliti ingin menentukan apakah data mereka terdistribusi normal. Hal ini penting karena banyak metode statistik, seperti uji t dan analisis varians, mengasumsikan bahwa data terdistribusi normal. Jika data tidak terdistribusi normal, hasil analisis ini dapat bias.
Terdapat berbagai uji normalitas yang dapat digunakan, masing-masing dengan kelebihan dan kekurangannya sendiri. Beberapa uji normalitas yang umum digunakan meliputi uji Shapiro-Wilk, uji Kolmogorov-Smirnov, dan uji Jarque-Bera. Pemilihan uji normalitas yang tepat tergantung pada ukuran sampel dan karakteristik data.
Cara Mengatasi Uji Normalitas di EViews
Dalam analisis data, uji normalitas digunakan untuk menentukan apakah data terdistribusi normal atau tidak. Distribusi normal adalah bentuk distribusi data yang simetris dan berbentuk lonceng. Jika data tidak terdistribusi normal, beberapa uji statistik mungkin tidak dapat digunakan atau hasilnya mungkin tidak akurat.
EViews adalah perangkat lunak statistik yang dapat digunakan untuk melakukan uji normalitas. Namun, terkadang uji normalitas di EViews mungkin gagal atau memberikan hasil yang tidak jelas. Dalam kasus ini, ada beberapa cara untuk mengatasi masalah tersebut.
Memeriksa Ukuran Sampel
Salah satu alasan paling umum mengapa uji normalitas gagal adalah karena ukuran sampel terlalu kecil. Ukuran sampel yang kecil dapat menyebabkan uji normalitas tidak dapat mendeteksi penyimpangan dari normalitas. Sebagai aturan umum, ukuran sampel minimal 50 dianggap cukup untuk uji normalitas.
Menggunakan Transformasi Data
Jika data tidak terdistribusi normal, transformasi data dapat digunakan untuk menormalkan data. Transformasi data adalah proses mengubah data dengan cara tertentu untuk membuat data lebih sesuai dengan distribusi normal. Ada beberapa jenis transformasi data yang dapat digunakan, seperti transformasi logaritma, transformasi kuadrat, atau transformasi akar kuadrat.
Menggunakan Uji Non-parametrik
Jika uji normalitas gagal dan transformasi data tidak dapat digunakan, uji non-parametrik dapat digunakan. Uji non-parametrik adalah uji statistik yang tidak bergantung pada asumsi bahwa data terdistribusi normal. Ada beberapa jenis uji non-parametrik yang dapat digunakan, seperti uji Wilcoxon, uji Kruskal-Wallis, atau uji Friedman.
Memeriksa Outlier, Cara mengatasi uji normalitas eviews
Outlier adalah data yang jauh berbeda dari data lainnya. Outlier dapat mempengaruhi hasil uji normalitas. Jika terdapat outlier dalam data, outlier dapat dihapus sebelum melakukan uji normalitas.
Menggunakan Perangkat Lunak Statistik Lainnya
Jika EViews tidak dapat mengatasi masalah uji normalitas, perangkat lunak statistik lainnya dapat digunakan. Ada beberapa perangkat lunak statistik lain yang dapat melakukan uji normalitas, seperti SPSS, SAS, atau R.
Diagram Alur
Proses pengambilan keputusan untuk memilih uji normalitas yang sesuai dapat diuraikan dalam diagram alur berikut:
Jenis Data
Pertama, tentukan jenis data yang Anda miliki:
- Data kuantitatif kontinu
- Data kuantitatif diskrit
- Data kualitatif
Ukuran Sampel
Selanjutnya, pertimbangkan ukuran sampel:
- Ukuran sampel besar (n > 50): Uji normalitas parametrik
- Ukuran sampel kecil (n<= 50): Uji normalitas non-parametrik
Distribusi Data
Terakhir, pertimbangkan distribusi data:
- Distribusi normal: Uji Jarque-Bera
- Distribusi tidak normal: Uji Shapiro-Wilk
Dengan mengikuti langkah-langkah ini, Anda dapat menentukan uji normalitas yang paling sesuai untuk data Anda.
Untuk mengatasi uji normalitas EViews, Anda dapat menggunakan berbagai metode seperti transformasi data atau uji alternatif. Namun, jika Anda beralih ke tugas teknis yang berbeda, seperti cara splicing kabel fo , Anda harus mengikuti langkah-langkah khusus. Proses splicing yang tepat memastikan koneksi serat optik yang andal dan berkelanjutan.
Setelah memahami cara splicing kabel fo, Anda dapat kembali ke analisis data Anda dan melanjutkan pengujian normalitas di EViews dengan pemahaman yang lebih komprehensif.
Contoh Kasus
Dalam sebuah studi kasus, data penjualan produk elektronik selama periode satu tahun dikumpulkan. Tujuan penelitian ini adalah untuk menentukan apakah data penjualan mengikuti distribusi normal.
Untuk menguji normalitas, uji Shapiro-Wilk digunakan. Uji ini mengukur seberapa dekat data dengan distribusi normal, dengan nilai p yang rendah menunjukkan penyimpangan yang signifikan dari normalitas.
Hasil Uji
Hasil uji Shapiro-Wilk menunjukkan nilai p sebesar 0,05. Nilai ini menunjukkan bahwa data penjualan tidak mengikuti distribusi normal secara signifikan pada tingkat signifikansi 5%.
Dampak pada Analisis
Ketidaknormalan data penjualan dapat berdampak pada analisis statistik lebih lanjut, seperti uji-t dan uji ANOVA. Dalam kasus seperti ini, disarankan untuk menggunakan uji statistik non-parametrik yang tidak bergantung pada asumsi normalitas.
Kesimpulan
Berdasarkan hasil uji Shapiro-Wilk, data penjualan tidak mengikuti distribusi normal. Hal ini perlu dipertimbangkan saat melakukan analisis statistik lebih lanjut dan menggunakan uji statistik non-parametrik yang sesuai.
Tips untuk Meningkatkan Normalitas Data
Untuk meningkatkan normalitas data, beberapa tips praktis dapat diterapkan. Pengumpulan data yang cermat sangat penting, memastikan bahwa data dikumpulkan secara representatif dan tidak mengandung kesalahan atau bias.
Selain itu, transformasi data dapat digunakan untuk mengubah distribusi data menjadi lebih normal. Transformasi umum termasuk transformasi logaritmik, transformasi kuadrat, dan transformasi akar kuadrat. Pemilihan transformasi yang sesuai bergantung pada sifat data dan tingkat non-normalitas.
Teknik Transformasi Data
- Transformasi Logaritmik:Mengubah data dengan mengambil logaritma, yang dapat menormalkan distribusi data yang miring ke kanan.
- Transformasi Kuadrat:Mengkuadratkan setiap titik data, yang dapat menormalkan distribusi data yang miring ke kiri.
- Transformasi Akar Kuadrat:Mengambil akar kuadrat dari setiap titik data, yang dapat menormalkan distribusi data yang terkonsentrasi di sekitar titik tengah.
Tips Tambahan
Selain teknik transformasi, tips tambahan untuk meningkatkan normalitas data meliputi:
- Menghilangkan data pencilan yang dapat mendistorsi distribusi.
- Menggunakan teknik pengambilan sampel yang tepat untuk memastikan bahwa data mewakili populasi yang lebih besar.
- Mempertimbangkan metode non-parametrik yang tidak memerlukan asumsi normalitas.
Perangkat Lunak Alternatif untuk Uji Normalitas
Selain EViews, terdapat perangkat lunak lain yang dapat digunakan untuk melakukan uji normalitas. Perangkat lunak ini menawarkan fitur dan kelebihan yang beragam, sehingga pengguna dapat memilih perangkat lunak yang paling sesuai dengan kebutuhan mereka.
SPSS
SPSS (Statistical Package for the Social Sciences) adalah perangkat lunak statistik yang banyak digunakan untuk berbagai analisis data, termasuk uji normalitas. SPSS menyediakan beberapa metode uji normalitas, seperti uji Kolmogorov-Smirnov dan uji Shapiro-Wilk.
SAS
SAS (Statistical Analysis System) adalah perangkat lunak statistik yang kuat yang juga dapat digunakan untuk uji normalitas. SAS menyediakan berbagai prosedur untuk menguji normalitas, seperti PROC UNIVARIATE dan PROC NPAR1WAY.
Minitab
Minitab adalah perangkat lunak statistik yang mudah digunakan yang menawarkan berbagai fitur untuk uji normalitas. Minitab menyediakan uji normalitas grafis, seperti plot Q-Q dan plot P-P, serta uji statistik, seperti uji Anderson-Darling dan uji Jarque-Bera.
R
R adalah perangkat lunak statistik sumber terbuka yang menyediakan banyak paket untuk uji normalitas. Paket-paket ini mencakup metode uji normalitas yang berbeda, seperti uji Shapiro-Wilk, uji Kolmogorov-Smirnov, dan uji Lilliefors.
Python
Python adalah bahasa pemrograman yang banyak digunakan untuk analisis data. Python menyediakan beberapa pustaka untuk uji normalitas, seperti pustaka SciPy dan pustaka Statsmodels. Pustaka-pustaka ini menyediakan berbagai metode uji normalitas, seperti uji Jarque-Bera dan uji Shapiro-Wilk.
Sumber Daya Tambahan untuk Uji Normalitas
Untuk memperdalam pemahaman Anda tentang uji normalitas, kami telah menyusun daftar sumber daya tambahan yang mencakup topik ini secara lebih mendalam.
Tabel berikut menyajikan berbagai sumber daya, mulai dari artikel hingga situs web, yang dapat membantu Anda memperoleh wawasan lebih lanjut tentang konsep dan aplikasi uji normalitas.
Artikel dan Buku
- Uji Normalitas: Panduan Langkah demi Langkah – Artikel komprehensif yang memberikan panduan terperinci tentang cara melakukan uji normalitas.
- Statistik Terapan: Uji Normalitas – Bab buku yang membahas berbagai metode uji normalitas dan interpretasi hasilnya.
- Statistik untuk Ilmu Sosial – Buku teks yang mencakup uji normalitas sebagai bagian dari bab tentang uji hipotesis.
Situs Web
- Statistik How To – Situs web yang menyediakan panduan tentang berbagai topik statistik, termasuk uji normalitas.
- Stat Trek – Situs web yang menawarkan penjelasan mendalam tentang uji normalitas dan aplikasi praktisnya.
- EViews Guide – Dokumentasi resmi untuk perangkat lunak EViews, yang mencakup penjelasan tentang uji normalitas yang tersedia dalam perangkat lunak tersebut.
Studi Kasus: Pengaruh Ketidaknormalan Data pada Regresi Linier
Ketidaknormalan data dapat berdampak signifikan pada hasil regresi linier. Data yang tidak normal dapat menyebabkan:
- Perkiraan koefisien yang bias
- Uji signifikansi yang tidak dapat diandalkan
- Prediksi yang tidak akurat
Transformasi Data
Transformasi data adalah teknik umum untuk mengatasi ketidaknormalan data. Transformasi ini mengubah distribusi data sehingga lebih mendekati distribusi normal. Beberapa transformasi umum meliputi:
- Logaritma
- Akar kuadrat
- Transformasi Box-Cox
Teknik Lainnya
Selain transformasi data, teknik lain yang dapat digunakan untuk mengatasi ketidaknormalan data meliputi:
- Pemangkasan data: Menghapus data yang sangat ekstrem
- Regresi yang kuat: Menggunakan metode estimasi yang tidak terpengaruh oleh data ekstrem
Contoh Kode
Berikut adalah contoh kode dalam EViews yang menunjukkan bagaimana mengatasi ketidaknormalan data menggunakan transformasi logaritma:
“`// Muat dataopen mydata.wf1// Uji normalitasnormalitytest y// Transformasi logaritmagen y_log = log(y)// Regresi linier dengan data yang ditransformasikanols y_log x1 x2 x3“`
Referensi
* [Pengaruh Ketidaknormalan Data pada Regresi Linier](https://stats.stackexchange.com/questions/20518/the-effect-of-non-normality-on-linear-regression)
[Mengatasi Ketidaknormalan Data dalam Regresi](https
//www.theanalysisfactor.com/dealing-with-non-normality-in-regression/)
Batasan Uji Normalitas
Meskipun uji normalitas sangat membantu dalam mengidentifikasi penyimpangan dari distribusi normal, namun terdapat beberapa keterbatasan yang perlu diperhatikan:
Ketergantungan pada Ukuran Sampel
Uji normalitas dapat dipengaruhi oleh ukuran sampel. Dengan sampel yang kecil, uji mungkin tidak dapat mendeteksi penyimpangan dari normalitas, sementara dengan sampel yang besar, uji mungkin menjadi terlalu sensitif dan mendeteksi penyimpangan kecil yang tidak signifikan.
Sensitivitas terhadap Pencilan
Uji normalitas sensitif terhadap pencilan. Pencilan dapat mendistorsi hasil uji dan membuat data tampak tidak normal, meskipun sebenarnya tidak.
Metode Alternatif untuk Menguji Normalitas
Selain uji normalitas parametrik, terdapat metode alternatif untuk menguji asumsi normalitas, seperti uji non-parametrik, seperti uji Shapiro-Wilk atau uji Kolmogorov-Smirnov.
Tabel Uji Normalitas
| Uji | Kelebihan | Kekurangan |
|---|---|---|
| Uji Jarak Chi-kuadrat | Sederhana untuk diterapkan | Sensitif terhadap ukuran sampel dan pencilan |
| Uji Jarak Kolmogorov-Smirnov | Tidak sensitif terhadap pencilan | Sulit untuk diterapkan dengan sampel besar |
| Uji Shapiro-Wilk | Berdaya tinggi untuk sampel kecil | Tidak sekuat uji lainnya untuk sampel besar |
| Uji Jarak Jarque-Bera | Menguji asimetri dan kurtosis | Sensitif terhadap pencilan |
Skenario Tidak Sesuai
Uji normalitas mungkin tidak sesuai dalam skenario berikut:
- Sampel sangat kecil atau sangat besar
- Data mengandung pencilan yang signifikan
- Data memiliki distribusi yang sangat miring atau kurtosis tinggi
Transformasi Data
Dalam kasus di mana data tidak berdistribusi normal, transformasi data dapat digunakan untuk menormalkan data. Transformasi umum meliputi:
- Transformasi logaritma
- Transformasi akar kuadrat
- Transformasi kotak
Implikasi Menggunakan Metode Statistik yang Mengasumsikan Normalitas
Menggunakan metode statistik yang mengasumsikan normalitas pada data yang tidak normal dapat menyebabkan hasil yang bias dan tidak dapat diandalkan. Oleh karena itu, penting untuk menguji asumsi normalitas sebelum menggunakan metode tersebut.
Simpulan Akhir
Dengan mengikuti panduan ini, Anda akan dapat melakukan uji normalitas EViews dengan percaya diri dan mengambil tindakan yang diperlukan untuk memastikan data Anda memenuhi asumsi normalitas. Ini akan memungkinkan Anda untuk melakukan analisis statistik yang valid dan membuat keputusan yang tepat berdasarkan data Anda.
Pertanyaan yang Sering Diajukan
Bagaimana cara melakukan uji normalitas di EViews?
Muat data Anda ke EViews, pilih variabel yang akan diuji, pilih jenis uji normalitas, dan tafsirkan hasilnya.
Apa jenis uji normalitas yang tersedia di EViews?
Shapiro-Wilk, Kolmogorov-Smirnov, Jarque-Bera, Anderson-Darling
Bagaimana cara menafsirkan hasil uji normalitas?
Tolak hipotesis nol jika nilai p kurang dari tingkat signifikansi.
Apa yang harus dilakukan jika data saya tidak terdistribusi normal?
Terapkan transformasi data, seperti log atau akar kuadrat, atau gunakan uji non-parametrik.