Menghitung bilangan oktal mungkin tampak menakutkan, tetapi sebenarnya tidak sesulit yang Anda bayangkan. Sistem bilangan oktal, yang menggunakan basis 8, sering digunakan dalam komputasi dan bidang teknis lainnya. Dalam panduan ini, kita akan menguraikan cara menghitung bilangan oktal, langkah demi langkah, untuk membantu Anda menguasai sistem bilangan yang menarik ini.
Dengan mengikuti langkah-langkah sederhana dan menggunakan tip praktis, Anda akan segera mengonversi bilangan oktal ke desimal dan sebaliknya, melakukan operasi aritmatika, dan memahami kegunaan bilangan oktal dalam dunia nyata. Jadi, mari kita mulai perjalanan kita untuk mengungkap misteri bilangan oktal!
– Jelaskan apa itu bilangan oktal.
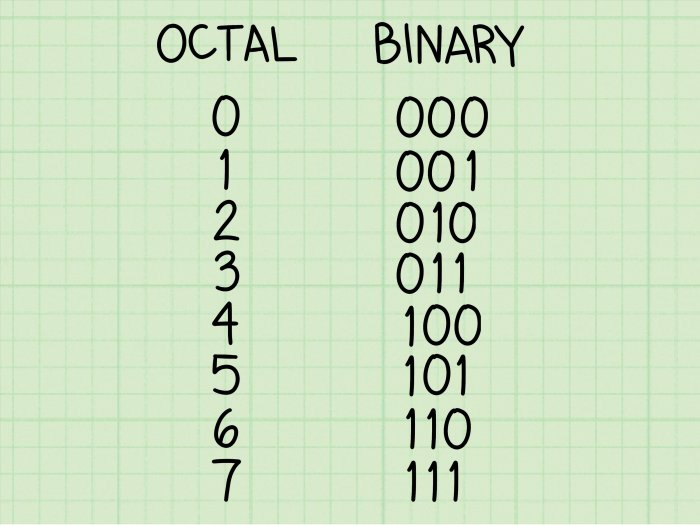
Bilangan oktal adalah sistem bilangan berbasis 8, yang berarti hanya menggunakan delapan digit (0, 1, 2, 3, 4, 5, 6, dan 7). Sistem ini banyak digunakan dalam komputasi, terutama di masa-masa awal karena kemudahannya dalam mengonversi antara sistem oktal dan biner.
Contoh bilangan oktal
Contoh bilangan oktal antara lain:
- 0 (desimal 0)
- 12 (desimal 10)
- 27 (desimal 23)
- 56 (desimal 46)
Konversi bilangan oktal ke desimal dan biner
Untuk mengonversi bilangan oktal ke desimal, kalikan setiap digit dengan pangkat 8 sesuai dengan posisinya, mulai dari kanan. Misalnya, untuk mengonversi 27 oktal ke desimal:
x 81+ 7 x 8 0= 16 + 7 = 23
Untuk mengonversi bilangan oktal ke biner, konversikan setiap digit oktal ke ekuivalen binernya (tiga digit) dan gabungkan hasilnya. Misalnya, untuk mengonversi 27 oktal ke biner:
(biner 010) + 7 (biner 111) = 010111
Tips untuk mengingat bilangan oktal
Ada beberapa tips yang dapat membantu mengingat bilangan oktal:
- Kelompokkan digit oktal menjadi tiga, mulai dari kanan.
- Konversikan setiap kelompok tiga digit oktal ke ekuivalen binernya.
- Hafalkan konversi biner untuk setiap kelompok tiga digit oktal.
Latihan soal
Konversikan bilangan oktal berikut ke desimal dan biner:
- 128
- 35 8
- 67 8
Konversi Bilangan Oktal ke Desimal
Bilangan oktal adalah sistem bilangan berbasis 8, yang menggunakan angka 0 hingga 7. Untuk mengonversi bilangan oktal ke desimal, kita perlu mengalikan setiap digit oktal dengan nilai tempatnya dan menjumlahkan hasilnya.
Langkah-langkah Konversi Oktal ke Desimal
- Tulis bilangan oktal yang akan dikonversi.
- Mulai dari digit paling kanan, kalikan setiap digit oktal dengan nilai tempatnya. Nilai tempat adalah 8n, di mana n adalah posisi digit dari kanan ke kiri.
- Jumlahkan semua hasil perkalian.
Contoh:
Konversikan bilangan oktal 753 ke desimal.
7 × 8 2+ 5 × 8 1+ 3 × 8 0= 448 + 40 + 3 = 491
Tabel Konversi Oktal ke Desimal
| Oktal | Desimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
Catatan:
- Untuk bilangan oktal yang memiliki lebih dari 8 digit, cukup lanjutkan mengalikan setiap digit dengan nilai tempatnya dan menjumlahkan hasilnya.
- Bilangan oktal dapat dikonversi ke sistem bilangan lainnya, seperti biner atau heksadesimal, dengan menggunakan konversi oktal ke desimal sebagai langkah pertama.
Konversi Bilangan Desimal ke Oktal
Konversi bilangan desimal ke oktal merupakan proses mengubah bilangan desimal (basis 10) menjadi bilangan oktal (basis 8). Proses ini dilakukan dengan membagi bilangan desimal secara berulang dengan 8 dan mencatat sisa pembagiannya.
Pembagian Berulang
Untuk mengonversi bilangan desimal ke oktal, ikuti langkah-langkah berikut:
- Bagilah bilangan desimal dengan 8 dan catat sisanya.
- Ulangi langkah 1 dengan membagi hasil bagi sebelumnya dengan 8 hingga hasil bagi menjadi 0.
- Sisa pembagian yang diperoleh dibaca dari bawah ke atas untuk membentuk bilangan oktal.
Contoh
Konversi bilangan desimal 25 ke oktal:
- 25 ÷ 8 = 3 sisa 1
- 3 ÷ 8 = 0 sisa 3
Jadi, 25 dalam oktal adalah 31.
Operasi Aritmatika pada Bilangan Oktal
Bilangan oktal, yang menggunakan basis 8, juga dapat digunakan dalam operasi aritmatika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan
Untuk menjumlahkan dua bilangan oktal, cukup tambahkan nilai tempat masing-masing dan konversi hasilnya ke bilangan oktal.
Pengurangan
Pengurangan bilangan oktal mirip dengan penjumlahan, tetapi kita mengurangi nilai tempat masing-masing dan mengonversi hasilnya ke bilangan oktal.
Perkalian
Perkalian bilangan oktal dilakukan dengan mengalikan setiap digit dari faktor pertama dengan setiap digit dari faktor kedua dan menjumlahkan hasilnya. Hasil setiap perkalian digit dikonversi ke bilangan oktal.
Pembagian
Pembagian bilangan oktal menggunakan metode yang mirip dengan pembagian bilangan desimal, di mana dividen dibagi dengan pembagi berulang kali dan hasilnya dikonversi ke bilangan oktal.
Penggunaan Bilangan Oktal
Bilangan oktal banyak digunakan dalam bidang komputasi karena kesederhanaannya dan kemudahannya dalam mengonversi antara bilangan oktal dan biner.
Sistem Operasi
Sistem operasi seperti Unix dan Linux menggunakan bilangan oktal untuk menentukan izin file dan direktori. Misalnya, izin 777 menunjukkan bahwa file atau direktori dapat dibaca, ditulis, dan dieksekusi oleh semua pengguna.
Bahasa Pemrograman
Bahasa pemrograman seperti C dan C++ menggunakan bilangan oktal untuk mewakili nilai konstanta dan nilai bitwise. Misalnya, nilai oktal 0177 mewakili bilangan desimal 127, dan nilai oktal 0x11 mewakili bilangan biner 00010001.
Mengolah serai untuk obat membutuhkan keterampilan khusus. Untuk menghasilkan ramuan obat yang efektif, cara mengolah serai harus dilakukan dengan benar. Sama halnya dengan menghitung bilangan oktal. Proses konversi bilangan desimal ke oktal memerlukan pemahaman konsep tertentu. Dimulai dengan membagi bilangan desimal dengan basis oktal (8), sisa pembagian selanjutnya digunakan untuk membentuk bilangan oktal.
– Jelaskan hubungan bilangan oktal dengan sistem bilangan lainnya (desimal, biner, heksadesimal) secara rinci.
Bilangan oktal merupakan sistem bilangan berbasis 8, di mana setiap digitnya mewakili nilai antara 0 dan 7. Sistem bilangan ini terkait erat dengan sistem bilangan biner (basis 2) dan heksadesimal (basis 16).
Konversi antara Oktal dan Biner
- Untuk mengonversi bilangan oktal ke biner, ubah setiap digit oktal ke ekuivalen biner 3-bitnya.
- Misalnya, oktal 735 = 111 011 101 biner.
Konversi antara Oktal dan Heksadesimal
- Untuk mengonversi bilangan oktal ke heksadesimal, ubah setiap 3 digit oktal ke ekuivalen heksadesimalnya.
- Misalnya, oktal 735 = 1E7 heksadesimal.
Konversi antara Oktal dan Desimal
- Untuk mengonversi bilangan oktal ke desimal, kalikan setiap digit dengan pangkat 8 yang sesuai, lalu jumlahkan hasilnya.
- Misalnya, oktal 735 = 7 x 8 2+ 3 x 8 1+ 5 x 8 0= 477 desimal.
| Oktal | Biner | Heksadesimal | Desimal |
|---|---|---|---|
| 0 | 000 | 0 | 0 |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
Penerapan Bilangan Oktal
- Sistem operasi Unix menggunakan bilangan oktal untuk menentukan izin file.
- Dalam pengkodean data, bilangan oktal digunakan untuk mewakili karakter khusus yang tidak dapat direpresentasikan dalam ASCII.
“Bilangan oktal memainkan peran penting dalam komputasi karena kesederhanaannya dalam mengonversi ke dan dari sistem bilangan biner, yang mendasari operasi komputer modern.”- Encyclopedia Britannica
Menghitung bilangan oktal itu mudah, hanya dengan mengubah setiap digit desimal menjadi ekivalen oktalnya. Nah, jika kamu sedang membuat es jelly, prosesnya juga cukup sederhana. Campurkan saja gula, air, dan bubuk agar-agar ( cara buat es jelly ). Setelah mendidih, tuangkan ke dalam cetakan dan dinginkan.
Menarik bukan? Sementara itu, kembali ke topik bilangan oktal, konversi dari desimal ke oktal hanya memerlukan beberapa langkah sederhana, memastikan kamu dapat menghitungnya dengan mudah.
Representasi Bilangan Oktal dalam Komputer
Dalam sistem komputer, bilangan oktal direpresentasikan menggunakan sistem bilangan basis 8, yang terdiri dari angka 0 hingga 7. Setiap digit dalam bilangan oktal mewakili pangkat 8, dengan digit paling kanan mewakili 8 0, digit berikutnya mewakili 8 1, dan seterusnya.
Konversi Bilangan Oktal ke Basis 10
Untuk mengonversi bilangan oktal ke basis 10, kalikan setiap digit dengan pangkat 8 yang sesuai, lalu jumlahkan hasilnya. Misalnya, bilangan oktal 527 dapat dikonversi ke basis 10 sebagai berikut:
- 5 x 8 2= 320
- 2 x 8 1= 16
- 7 x 8 0= 7
- Jumlah = 320 + 16 + 7 = 343
Konversi Bilangan Basis 10 ke Oktal
Untuk mengonversi bilangan basis 10 ke oktal, bagi bilangan tersebut dengan 8 berulang kali dan catat sisa pembagian. Sisa pembagian ini dibaca dari belakang untuk mendapatkan bilangan oktal.
Misalnya, bilangan basis 10 343 dapat dikonversi ke oktal sebagai berikut:
- 343 ÷ 8 = 42 sisa 7
- 42 ÷ 8 = 5 sisa 2
- 5 ÷ 8 = 0 sisa 5
Dengan membaca sisa pembagian dari belakang, diperoleh bilangan oktal 527.
Penyimpanan Bilangan Oktal dalam Komputer
Dalam komputer, bilangan oktal disimpan menggunakan sistem komplemen dua. Setiap digit oktal diwakili oleh 3 bit, dan bit paling signifikan digunakan untuk mewakili tanda (0 untuk positif, 1 untuk negatif). Misalnya, bilangan oktal 527 akan disimpan sebagai berikut:
| Digit Oktal | Representasi Biner |
|---|---|
| 5 | 010 |
| 2 | 001 |
| 7 | 111 |
Representasi biner lengkapnya adalah 010001111.
Perhitungan Manual Bilangan Oktal
Dalam sistem bilangan oktal, setiap angka mewakili delapan nilai (0 hingga 7). Perhitungan manual bilangan oktal mengikuti prinsip konversi bilangan desimal ke oktal atau sebaliknya.
Konversi Desimal ke Oktal
- Bagi angka desimal dengan 8.
- Tuliskan sisa pembagian sebagai angka oktal pertama.
- Bagi hasil bagi dengan 8 dan ulangi proses.
- Lanjutkan hingga hasil bagi menjadi 0.
- Susun angka oktal yang diperoleh secara terbalik.
Konversi Oktal ke Desimal
- Kalikan angka oktal paling kanan dengan 8 0.
- Kalikan angka oktal berikutnya dengan 8 1, dan seterusnya.
- Jumlahkan hasil perkalian untuk mendapatkan angka desimal.
Tabel Konversi
| Oktal | Desimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
Contoh Soal
- Konversikan 15 desimal ke oktal:
- Konversikan 27 oktal ke desimal:
Konversi 15 desimal ke oktal:
- 15 ÷ 8 = 1 sisa 7 (7)
- 1 ÷ 8 = 0 sisa 1 (1)
Hasil: 17 oktal Konversi 27 oktal ke desimal:
- 2 x 81= 16
- 7 x 8 0= 7
Hasil: 23 desimal
Tips
- Gunakan kalkulator jika memungkinkan.
- Hafalkan tabel konversi.
- Periksa hasil perhitungan secara hati-hati.
Alat Bantu Konversi Bilangan Oktal
Untuk memudahkan konversi bilangan oktal, tersedia berbagai alat bantu yang dapat membantu. Alat-alat ini menawarkan fitur dan tingkat akurasi yang beragam, sehingga penting untuk memilih alat yang sesuai dengan kebutuhan Anda.
Daftar Alat Bantu Konversi Bilangan Oktal
- Kalkulator Online:Situs web seperti Calculator.net dan Convert Units menyediakan kalkulator online gratis yang dapat mengonversi bilangan oktal ke desimal dan sebaliknya.
- Aplikasi Ponsel:Tersedia aplikasi ponsel, seperti Octal Converter untuk Android dan Octal Converter untuk iOS, yang menawarkan konversi bilangan oktal dengan cepat dan mudah.
- Perangkat Lunak Desktop:Perangkat lunak desktop, seperti Number Empire Octal Converter , dapat diinstal pada komputer Anda dan memberikan fungsionalitas konversi yang lebih komprehensif.
- Ekstensi Peramban:Ekstensi peramban, seperti Octal Decimal Converter untuk Chrome, memungkinkan Anda mengonversi bilangan oktal langsung dari bilah alamat peramban.
Perbandingan Alat Bantu Konversi Bilangan Oktal
| Fitur | Kalkulator Online | Aplikasi Ponsel | Perangkat Lunak Desktop | Ekstensi Peramban |
|---|---|---|---|---|
| Akurasi | Tinggi | Tinggi | Tinggi | Tinggi |
| Kemudahan Penggunaan | Mudah | Mudah | Cukup Mudah | Mudah |
| Kecepatan | Cepat | Cepat | Sedang | Cepat |
| Fitur Tambahan | Konversi bilangan lain | Konversi offline | Opsi penyesuaian | Konversi cepat |
Contoh Penggunaan
Misalnya, untuk mengonversi bilangan oktal 123 ke desimal menggunakan kalkulator online, cukup masukkan 123 ke dalam bidang input dan klik tombol “Convert”. Hasilnya, 83, akan ditampilkan di bidang output.
Praktik Terbaik
Saat menggunakan alat bantu konversi bilangan oktal, ada beberapa praktik terbaik yang harus diikuti:
- Verifikasi hasil konversi dengan metode lain.
- Gunakan alat bantu yang akurat dan andal.
- Pahami sistem bilangan oktal sebelum melakukan konversi.
Konversi Bilangan Oktal dalam Berbagai Basis
Bilangan oktal, yang menggunakan basis 8, dapat dikonversi ke basis bilangan lainnya dengan mengikuti langkah-langkah tertentu. Konversi ini berguna dalam berbagai aplikasi, seperti pemrograman komputer dan teknik elektronik.
Konversi ke Basis 2 (Biner)
Untuk mengonversi bilangan oktal ke biner, ubah setiap digit oktal menjadi representasi biner 3-bitnya. Misalnya, untuk mengonversi 123 8ke biner:
- 1 8= 001 2
- 2 8= 010 2
- 3 8= 011 2
Dengan menggabungkan representasi biner, kita mendapatkan 123 8= 001010011 2.
Konversi ke Basis 4 (Kuartener)
Untuk mengonversi bilangan oktal ke kuartener, ubah setiap digit oktal menjadi representasi kuartener 2-bitnya. Misalnya, untuk mengonversi 25 8ke kuartener:
- 2 8= 10 4
- 5 8= 13 4
Dengan menggabungkan representasi kuartener, kita mendapatkan 25 8= 1013 4.
Konversi ke Basis 16 (Heksadesimal)
Untuk mengonversi bilangan oktal ke heksadesimal, ubah setiap tiga digit oktal menjadi representasi heksadesimal 1-digitnya. Misalnya, untuk mengonversi 675 8ke heksadesimal:
- 6 8= 6 16
- 7 8= 7 16
- 5 8= 5 16
Dengan menggabungkan representasi heksadesimal, kita mendapatkan 675 8= 675 16.
Menghitung bilangan oktal tidaklah rumit. Sama seperti menghitung dalam sistem bilangan desimal, Anda cukup membagi angka dengan 8 berulang kali dan mencatat sisanya. Untuk mendapatkan hasil akhir, gabungkan sisa-sisa tersebut dalam urutan terbalik. Nah, jika Anda sedang mencari cara untuk mendapatkan uang 1 milyar secara gratis, ada beberapa tips yang bisa Anda coba di cara dapat uang 1 milyar gratis . Namun, jangan lupa untuk terus mengasah kemampuan Anda dalam menghitung bilangan oktal, karena ini merupakan keterampilan dasar yang berguna dalam berbagai bidang sains dan teknologi.
Penerapan Bilangan Oktal dalam Bidang Teknis
Bilangan oktal memiliki peran penting dalam berbagai bidang teknis, seperti elektronik, telekomunikasi, dan jaringan komputer. Keunikan sistem bilangan ini menjadikannya pilihan yang tepat untuk mewakili data biner secara ringkas dan efisien.
Elektronik
- Perancangan sirkuit digital: Bilangan oktal digunakan untuk mewakili nilai-nilai biner pada diagram skema dan dokumentasi teknis, memudahkan pemahaman dan pembacaan.
- Konversi sinyal: Dalam konversi analog-ke-digital (ADC) dan digital-ke-analog (DAC), bilangan oktal membantu menyederhanakan proses konversi dengan mengurangi jumlah bit yang diperlukan.
Telekomunikasi
- Transmisi data: Bilangan oktal digunakan untuk mewakili alamat IP dan MAC, yang mengidentifikasi perangkat dalam jaringan. Ini menyederhanakan pengelolaan jaringan dan penyelesaian masalah.
- Sistem telepon: Kode oktal digunakan dalam sistem telepon lama untuk mewakili nomor telepon, yang memberikan kemudahan dalam mengingat dan transmisi.
Jaringan Komputer
- Pengkodean data: Bilangan oktal digunakan dalam pengkodean karakter ASCII dan Unicode, yang memungkinkan representasi data teks dan non-teks.
- Sistem file: Sistem file tertentu, seperti FAT12 dan FAT16, menggunakan bilangan oktal untuk mewakili izin file dan atribut lainnya.
Tantangan dalam Penghitungan Bilangan Oktal
Penghitungan bilangan oktal, yang menggunakan basis 8, dapat menimbulkan beberapa tantangan:
Kesalahan Konversi
Kesalahan konversi umum terjadi saat menerjemahkan bilangan oktal ke sistem bilangan lain (misalnya, desimal, heksadesimal). Kesalahan ini dapat disebabkan oleh kekeliruan dalam mengidentifikasi digit oktal atau kesalahan penghitungan.
Dalam dunia bilangan, menghitung bilangan oktal adalah tugas yang menarik. Dengan menggunakan sistem bilangan berbasis 8, bilangan oktal memungkinkan representasi yang lebih ringkas dibandingkan dengan bilangan desimal. Namun, bagi pecinta kuliner, mari kita beralih sejenak ke dunia kuliner dengan menjajal resep cara buat jenang grendul , makanan tradisional Jawa yang manis dan legit.
Proses pembuatannya yang sederhana dan bahan-bahan yang mudah didapat menjadikan jenang grendul pilihan tepat untuk disantap bersama keluarga. Kembali ke dunia matematika, memahami cara menghitung bilangan oktal akan membuka wawasan baru dalam eksplorasi sistem bilangan yang berbeda.
Keterbatasan Representasi
Sistem bilangan oktal memiliki keterbatasan dalam merepresentasikan bilangan tertentu, terutama bilangan pecahan dan bilangan negatif. Representasi ini dapat menghasilkan hasil yang tidak tepat atau ambigu.
Solusi yang Diusulkan
Untuk mengatasi tantangan ini, disarankan untuk:
- Menggunakan algoritma konversi yang andal dan teruji.
- Melakukan pemeriksaan silang hasil konversi untuk meminimalkan kesalahan.
- Menjelajahi representasi alternatif untuk bilangan pecahan dan negatif, seperti bilangan oktal terapung.
Contoh Kode
Dalam bahasa pemrograman Python, konversi bilangan oktal ke desimal dapat dilakukan menggunakan fungsi `int()`: def oct_to_dec(octal): return int(octal, 8)octal_num = '123'decimal_num = oct_to_dec(octal_num)print(decimal_num) # Output: 83
Praktik Terbaik
Untuk penghitungan bilangan oktal yang akurat dan efisien, praktik terbaik meliputi:
- Menggunakan konvensi penamaan yang jelas dan konsisten untuk variabel dan fungsi.
- Memvalidasi input pengguna untuk memastikan bilangan oktal yang valid.
- Menangani kasus khusus, seperti bilangan oktal terkemuka dan angka nol.
Tren dan Perkembangan dalam Penghitungan Bilangan Oktal
Penghitungan bilangan oktal terus mengalami kemajuan seiring dengan perkembangan teknologi dan kebutuhan akan metode konversi yang lebih efisien. Tren terkini berfokus pada pengembangan algoritma yang lebih cepat dan teknik yang menyederhanakan proses konversi.
Teknik Konversi yang Lebih Efisien
Teknik konversi yang lebih efisien seperti penggunaan tabel pencarian dan algoritma berbasis rekursi telah dikembangkan untuk mempercepat proses konversi. Tabel pencarian menyimpan nilai konversi yang telah dihitung sebelumnya, memungkinkan pengambilan cepat ketika diperlukan. Algoritma berbasis rekursi membagi masalah konversi menjadi sub-masalah yang lebih kecil, yang kemudian diselesaikan secara rekursif, menghasilkan konversi yang lebih cepat.
Algoritma Perhitungan yang Lebih Cepat
Algoritma perhitungan yang lebih cepat, seperti Algoritma Booth dan Algoritma Karatsuba, telah dikembangkan untuk meningkatkan kecepatan perhitungan aritmatika bilangan oktal. Algoritma Booth memanfaatkan sifat komplemen dua bilangan oktal untuk mengurangi jumlah langkah perhitungan. Algoritma Karatsuba menggunakan pendekatan bagi-dan-taklukkan untuk memecah masalah perkalian menjadi sub-masalah yang lebih kecil, yang mengarah pada pengurangan waktu komputasi.
Kesalahan Umum dalam Penghitungan Bilangan Oktal
Penghitungan bilangan oktal mengharuskan ketelitian untuk menghindari kesalahan yang dapat berdampak signifikan pada hasil akhir. Berikut beberapa kesalahan umum yang sering terjadi dan cara menghindarinya:
Kesalahan Konversi
Kesalahan konversi muncul saat mengubah bilangan oktal ke basis lain atau sebaliknya. Hindari kesalahan ini dengan:
- Pastikan setiap digit oktal valid (0-7).
- Gunakan tabel konversi atau kalkulator yang andal.
- Periksa ulang hasil konversi dengan cermat.
Kesalahan Operasi Aritmatika
Operasi aritmatika pada bilangan oktal harus dilakukan dengan hati-hati. Kesalahan umum meliputi:
- Melupakan mengonversi bilangan ke basis yang sama sebelum melakukan operasi.
- Tidak menggunakan bobot posisi yang benar saat menjumlahkan atau mengurangkan.
- Tidak mengikuti urutan operasi dengan benar (misalnya, perkalian dan pembagian dilakukan sebelum penjumlahan dan pengurangan).
Tips Menghindari Kesalahan, Cara menghitung bilangan oktal
Untuk meminimalkan kesalahan, ikuti tips ini:
- Pahami konsep sistem bilangan oktal dan bobot posisinya.
- Gunakan kalkulator atau alat konversi yang andal.
- Periksa ulang setiap langkah perhitungan.
- Berlatih soal secara teratur untuk meningkatkan keterampilan.
Contoh Kesalahan
*
-*Kesalahan Konversi
Mengonversi bilangan oktal 123 ke desimal sebagai 132 (harus 83).
-*Kesalahan Operasi Aritmatika
Menjumlahkan 123 oktal dan 45 oktal sebagai 168 oktal (harus 170 oktal).
Pemungkas
Setelah mempelajari panduan ini, Anda akan dilengkapi dengan pemahaman yang komprehensif tentang penghitungan bilangan oktal. Baik Anda seorang pelajar, programmer, atau penggemar matematika, pengetahuan ini akan menjadi aset berharga dalam bidang komputasi dan banyak lagi. Dengan latihan yang teratur, Anda akan menjadi ahli dalam mengonversi, menghitung, dan menerapkan bilangan oktal dengan percaya diri.
FAQ Terkini: Cara Menghitung Bilangan Oktal
Apa itu bilangan oktal?
Bilangan oktal adalah sistem bilangan yang menggunakan basis 8, artinya hanya memiliki 8 digit (0-7).
Bagaimana cara mengonversi bilangan oktal ke desimal?
Kalikan setiap digit oktal dengan pangkat 8 yang sesuai, lalu jumlahkan hasilnya.
Apa kegunaan bilangan oktal?
Bilangan oktal sering digunakan dalam komputasi karena dapat mewakili bilangan biner dengan cara yang lebih ringkas.