RPP Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018

RPP Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018 menjadi kunci keberhasilan pembelajaran matematika di kelas enam. Dokumen ini bukan sekadar kumpulan materi, melainkan peta jalan yang memandu guru dan siswa dalam perjalanan menaklukkan dunia angka dan rumus. Bagaimana RPP ini dirancang agar pembelajaran matematika menjadi menyenangkan dan mudah dipahami? Mari kita telusuri lebih dalam.

RPP ini mencakup berbagai aspek penting, mulai dari perencanaan pembelajaran yang matang hingga evaluasi dan refleksi yang mendalam. Struktur RPP yang terorganisir dengan baik, sesuai dengan Kurikulum 2013 Revisi 2018, memastikan keselarasan antara kompetensi dasar, indikator, tujuan pembelajaran, materi, metode, dan penilaian. Pembahasan materi mencakup pecahan, operasi hitung, bangun ruang, persentase, dan masih banyak lagi, semuanya dikaitkan dengan kehidupan sehari-hari untuk meningkatkan pemahaman dan daya guna siswa.

Struktur RPP Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018

Rancangan Pelaksanaan Pembelajaran (RPP) merupakan panduan bagi guru dalam melaksanakan proses pembelajaran. Kurikulum 2013 Revisi 2018 menekankan pembelajaran yang aktif, kreatif, efektif, dan menyenangkan. Oleh karena itu, RPP yang baik harus mencerminkan prinsip-prinsip tersebut dan disesuaikan dengan karakteristik peserta didik kelas 6.

Berikut ini pemaparan mendalam mengenai struktur dan komponen RPP Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018, dengan contoh-contoh konkret untuk memudahkan pemahaman.

Contoh RPP Matematika Kelas 6 Semester 2: Pecahan Senilai

Berikut contoh RPP untuk materi Pecahan dengan tema “Pecahan Senilai”, meliputi tiga kegiatan pembelajaran yang bervariasi: diskusi kelompok, permainan edukatif, dan presentasi.

RPP ini akan mencakup: Identifikasi Kompetensi Dasar (KD), Indikator Pencapaian Kompetensi, Tujuan Pembelajaran, Materi Pembelajaran, Metode Pembelajaran, Media Pembelajaran, Langkah-langkah Kegiatan Pembelajaran (dengan alokasi waktu), Penilaian (termasuk instrumen dan kriteria), dan Sumber Belajar. Detailnya akan meliputi penjelasan tentang cara menentukan pecahan senilai, contoh soal dan penyelesaiannya, serta kegiatan untuk memperkuat pemahaman siswa. Permainan edukatif seperti tebak pecahan senilai akan digunakan untuk meningkatkan partisipasi dan antusiasme siswa.

Diskusi kelompok akan memfasilitasi kolaborasi dan pemecahan masalah, sementara presentasi akan mengasah kemampuan komunikasi matematis siswa.

Kerangka RPP Matematika Kelas 6 Semester 2: Operasi Hitung Pecahan

Kerangka RPP ini akan menjabarkan secara detail komponen-komponen penting, mulai dari Kompetensi Dasar (KD) hingga sumber belajar, untuk materi Operasi Hitung Pecahan (Penjumlahan dan Pengurangan). Contoh soal dan kunci jawaban akan disertakan untuk memberikan gambaran konkret tentang materi yang diajarkan. Metode pembelajaran yang akan digunakan akan menekankan pada pendekatan aktif dan partisipatif, seperti diskusi kelompok dan pemecahan masalah.

Tabel berikut ini akan memberikan gambaran umum struktur RPP:

Komponen RPP	Fungsi	Contoh pada RPP Pecahan
Kompetensi Dasar (KD)	Menentukan standar kompetensi yang harus dicapai siswa.	3.6 Menentukan keliling dan luas persegi panjang. 4.6 Menyelesaikan masalah yang berkaitan dengan keliling dan luas persegi panjang.
Indikator	Menjabarkan KD menjadi butir-butir yang lebih spesifik dan terukur.	Siswa mampu menentukan pecahan senilai dengan benar.
Tujuan Pembelajaran	Menyatakan apa yang diharapkan siswa capai setelah pembelajaran.	Siswa dapat menjelaskan konsep pecahan senilai dan menentukan beberapa pecahan senilai dari suatu pecahan.
Materi Pembelajaran	Materi yang akan diajarkan kepada siswa.	Konsep pecahan senilai, contoh soal dan penyelesaiannya.
Metode Pembelajaran	Cara guru menyampaikan materi pembelajaran.	Diskusi kelompok, permainan edukatif, presentasi.
Media Pembelajaran	Alat bantu yang digunakan dalam pembelajaran.	Kartu pecahan, gambar, LCD proyektor.
Langkah-langkah Kegiatan Pembelajaran	Urutan kegiatan pembelajaran dengan alokasi waktu.	Pendahuluan (10 menit), Kegiatan Inti (60 menit), Penutup (10 menit).
Penilaian	Cara mengukur pencapaian siswa.	Tes tertulis, observasi, penilaian portofolio.
Sumber Belajar	Referensi yang digunakan guru dan siswa.	Buku teks, internet, modul.

Perbandingan Struktur RPP Kurikulum 2013 Revisi 2018 dengan KTSP 2006

Berikut perbandingan struktur RPP Kurikulum 2013 Revisi 2018 dengan KTSP 2006 pada beberapa aspek kunci. Perbedaan ini mencerminkan perubahan paradigma pembelajaran yang lebih menekankan pada pengembangan kompetensi siswa secara holistik.

Aspek	Kurikulum 2013 Revisi 2018	KTSP 2006
Komponen Utama	KD, Indikator, Tujuan Pembelajaran, Materi Pembelajaran, Metode Pembelajaran, Media Pembelajaran, Langkah-langkah Kegiatan Pembelajaran, Penilaian, Sumber Belajar.	Standar Kompetensi, Kompetensi Dasar, Indikator, Materi Pembelajaran, Kegiatan Pembelajaran, Penilaian.
Penekanan Pembelajaran	Pembelajaran aktif, kreatif, efektif, dan menyenangkan; berpusat pada siswa.	Pembelajaran terstruktur, berpusat pada guru.
Alokasi Waktu	Lebih fleksibel, disesuaikan dengan kebutuhan siswa.	Lebih kaku, terjadwal ketat.
Penilaian	Holistic, meliputi aspek kognitif, afektif, dan psikomotorik.	Terutama kognitif.
Integrasi Nilai	Terintegrasi dalam seluruh komponen RPP.	Seringkali terpisah dari materi pembelajaran.

Langkah-Langkah Penyusunan RPP Matematika Kelas 6: Pengukuran Sudut

Berikut langkah-langkah penyusunan RPP Matematika Kelas 6 untuk materi pengukuran sudut, beserta estimasi waktu penyusunan setiap langkah. Proses ini membutuhkan perencanaan yang matang dan pemahaman yang mendalam terhadap materi dan karakteristik siswa.

Ilustrasi flowchart akan memberikan gambaran visual tentang alur penyusunan RPP. Flowchart tersebut akan menampilkan urutan langkah-langkah penyusunan RPP, mulai dari penentuan KD dan Indikator hingga penyusunan instrumen penilaian. Setiap langkah akan disertai dengan estimasi waktu yang dibutuhkan untuk penyelesaiannya. Contohnya, penentuan KD dan Indikator mungkin membutuhkan waktu sekitar 30 menit, sedangkan pengembangan materi pembelajaran dan kegiatan pembelajaran dapat memakan waktu lebih lama, misalnya 2-3 jam.

Contoh Kalimat Tujuan Pembelajaran: Keliling dan Luas Persegi Panjang

Berikut lima contoh kalimat Tujuan Pembelajaran yang menggunakan kata kerja operasional untuk materi “Menentukan Keliling dan Luas Persegi Panjang”. Kata kerja operasional yang dipilih harus terukur dan dapat diamati untuk memastikan tujuan pembelajaran tercapai.

• Setelah mengikuti pembelajaran, siswa mampu menghitung keliling persegi panjang dengan benar.
• Siswa dapat menentukan luas persegi panjang dengan menggunakan rumus yang tepat.
• Siswa mampu menyelesaikan soal cerita yang berkaitan dengan keliling persegi panjang.
• Siswa dapat membedakan rumus keliling dan luas persegi panjang.
• Siswa mampu menggambar persegi panjang dan menghitung keliling serta luasnya.

Contoh Soal Evaluasi: Keliling dan Luas Persegi Panjang

Berikut contoh soal evaluasi untuk mengukur pencapaian KD 3.6 (menentukan keliling dan luas persegi panjang) dan KD 4.6 (menyelesaikan masalah yang berkaitan dengan keliling dan luas persegi panjang), beserta kunci jawaban dan pedoman penskoran. Soal-soal ini dirancang untuk menguji pemahaman konseptual dan kemampuan aplikasi siswa.

1. Hitunglah keliling persegi panjang dengan panjang 12 cm dan lebar 8 cm!
2. Sebuah persegi panjang memiliki luas 60 cm². Jika panjangnya 12 cm, berapakah lebarnya?
3. Sebuah taman berbentuk persegi panjang dengan panjang 20 meter dan lebar 15 meter. Berapa meter keliling taman tersebut?
4. Ibu membuat kue berbentuk persegi panjang dengan panjang 30 cm dan lebar 20 cm. Berapa cm² luas kue tersebut?
5. Andi akan membuat pagar di sekeliling kebunnya yang berbentuk persegi panjang dengan ukuran panjang 15 m dan lebar 10 m. Berapa meter panjang pagar yang dibutuhkan Andi?

Kunci Jawaban dan Pedoman Penskoran: (Akan disertakan detail kunci jawaban dan pedoman penskoran untuk setiap soal. Setiap soal bernilai 20 poin, sehingga total nilai adalah 100 poin.)

Materi Pembelajaran Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018

Semester 2 kelas 6 SD/MI menawarkan materi matematika yang membangun pemahaman lebih lanjut dari semester sebelumnya. Materi ini dirancang untuk mempersiapkan siswa menghadapi tantangan akademik selanjutnya dan diaplikasikan dalam kehidupan sehari-hari. Berikut uraian detail materi Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018.

Rincian Materi Pokok dan Sub-Materi

Tabel berikut merinci materi pokok, Kompetensi Dasar (KD), dan sub-materi Matematika kelas 6 semester 2. Kompetensi Dasar dirumuskan berdasarkan Kurikulum 2013 Revisi 2018. Perlu diingat bahwa KD yang tertera merupakan contoh dan bisa berbeda sedikit tergantung penerapan di sekolah masing-masing.

Pokok Bahasan	KD	Sub-Materi
Pecahan	3.6.1 dan 4.6.1 (Contoh KD, bisa berbeda di sekolah lain)	Operasi hitung pecahan (penjumlahan, pengurangan, perkalian, pembagian), pecahan desimal, persen
Bangun Ruang	3.6.2 dan 4.6.2 (Contoh KD, bisa berbeda di sekolah lain)	Kubus, balok, prisma segitiga, limas segitiga, luas permukaan dan volume
Persentase dan Bunga Tunggal	3.6.3 dan 4.6.3 (Contoh KD, bisa berbeda di sekolah lain)	Menghitung persentase, diskon, keuntungan, kerugian, bunga tunggal
Statistika	3.6.4 dan 4.6.4 (Contoh KD, bisa berbeda di sekolah lain)	Modus, median, mean dari data tunggal dan kelompok

Sub-Materi dan Penerapannya dalam Kehidupan Sehari-hari

Matematika kelas 6 semester 2 memiliki banyak materi yang relevan dengan kehidupan sehari-hari. Berikut beberapa contohnya:

Sub-Materi	Contoh Penerapan 1	Contoh Penerapan 2
Persentase Diskon	Menghitung diskon barang saat belanja di supermarket.	Membandingkan harga barang yang sedang diskon di dua toko berbeda.
Bunga Tunggal	Menghitung bunga tabungan di bank.	Menganalisis keuntungan investasi jangka pendek.
Volume Balok	Menghitung volume air dalam akuarium.	Menghitung volume pasir yang dibutuhkan untuk mengisi kotak pasir.
Menghitung Rata-rata (Mean)	Menghitung nilai rata-rata ulangan harian.	Menghitung rata-rata tinggi badan siswa dalam satu kelas.

Kaitan Antar Materi

Materi Matematika kelas 6 semester 2 saling berkaitan. Pemahaman konsep pecahan misalnya, sangat penting untuk memahami persentase dan perhitungan volume bangun ruang. Berikut gambaran alur keterkaitan antar materi:

Pecahan → Persentase (Pecahan digunakan untuk menghitung persentase) → Bunga Tunggal (Persentase digunakan untuk menghitung bunga tunggal)
Pecahan → Volume Bangun Ruang (Pecahan digunakan dalam perhitungan volume)
Persentase → Keuntungan/Kerugian (Persentase digunakan untuk menghitung keuntungan atau kerugian)

Bangun Ruang Sisi Datar

Berikut penjelasan mengenai bangun ruang sisi datar, meliputi kubus, balok, prisma segitiga, dan limas segitiga. Penjelasan meliputi jumlah sisi, rusuk, titik sudut, rumus luas permukaan dan volume, serta contoh benda nyata yang menyerupai bangun ruang tersebut.

Nama Bangun Ruang	Ilustrasi	Sifat-Sifat	Contoh Benda Nyata
Kubus	Bayangkan sebuah kotak dengan 6 sisi persegi yang sama besar, 12 rusuk yang sama panjang, dan 8 titik sudut.	6 sisi, 12 rusuk, 8 titik sudut, Luas Permukaan = 6s², Volume = s³ (s = panjang sisi)	Dadu, kotak penyimpanan
Balok	Bayangkan sebuah kotak dengan 6 sisi persegi panjang (tiga pasang sisi yang berhadapan sama besar), 12 rusuk (empat rusuk yang berhadapan sama panjang), dan 8 titik sudut.	6 sisi, 12 rusuk, 8 titik sudut, Luas Permukaan = 2(pl + pt + lt), Volume = p x l x t (p = panjang, l = lebar, t = tinggi)	Buku, kardus sepatu
Prisma Segitiga	Bayangkan dua segitiga kongruen sebagai alas dan atas, dihubungkan oleh tiga persegi panjang sebagai sisi tegak.	5 sisi, 9 rusuk, 6 titik sudut, Luas Permukaan dan Volume rumusnya lebih kompleks dan akan dipelajari di tingkat selanjutnya.	Rumah tenda, atap miring
Limas Segitiga	Bayangkan sebuah segitiga sebagai alas dan tiga segitiga sebagai sisi tegak yang bertemu pada satu titik puncak.	4 sisi, 6 rusuk, 4 titik sudut, Luas Permukaan dan Volume rumusnya lebih kompleks dan akan dipelajari di tingkat selanjutnya.	Piramida (bentuk sederhana), beberapa jenis atap rumah

Soal Cerita Persentase dan Bunga Tunggal

Berikut contoh soal cerita persentase dan bunga tunggal dengan tingkat kesulitan berbeda.

> Soal 1 (Mudah): Seorang pedagang membeli 100 buah mangga dengan harga Rp 500.000. Kemudian ia menjualnya dengan harga Rp 6.000 per buah. Berapa persen keuntungan yang diperoleh pedagang tersebut?>> Penyelesaian: Total penjualan = 100 buah x Rp 6.000/buah = Rp 600.000. Keuntungan = Rp 600.000 – Rp 500.000 = Rp 100.000. Persentase keuntungan = (Keuntungan / Harga Beli) x 100% = (Rp 100.000 / Rp 500.000) x 100% = 20%>> Jawaban: 20%>> Soal 2 (Sedang): Ani menabung uang sebesar Rp 2.000.000 di bank dengan bunga tunggal 5% per tahun.

Berapa jumlah uang Ani setelah 2 tahun?>> Penyelesaian: Bunga per tahun = Rp 2.000.000 x 5% = Rp 100.000. Bunga selama 2 tahun = Rp 100.000 x 2 = Rp 200.000. Jumlah uang Ani setelah 2 tahun = Rp 2.000.000 + Rp 200.000 = Rp 2.200.000>> Jawaban: Rp 2.200.000>> Soal 3 (Sulit): Sebuah toko memberikan diskon 20% untuk semua barang.

Budi membeli sebuah baju seharga Rp 250.000 dan celana seharga Rp 300.000. Jika Budi membayar dengan uang Rp 600.000, berapa uang kembalian yang diterima Budi?>> Penyelesaian: Diskon baju = Rp 250.000 x 20% = Rp 50.000. Harga baju setelah diskon = Rp 250.000 – Rp 50.000 = Rp 200.000. Diskon celana = Rp 300.000 x 20% = Rp 60.000.

Harga celana setelah diskon = Rp 300.000 – Rp 60.000 = Rp 240.000. Total harga setelah diskon = Rp 200.000 + Rp 240.000 = Rp 440.000. Uang kembalian = Rp 600.000 – Rp 440.000 = Rp 160.000>> Jawaban: Rp 160.000

Metode Pembelajaran Matematika Kelas 6 Semester 2

Pemilihan metode pembelajaran yang tepat sangat krusial dalam keberhasilan proses belajar mengajar matematika di kelas 6 semester 2. Materi semester ini cenderung lebih kompleks, meliputi perbandingan, skala, pengukuran sudut, volume bangun ruang, pecahan, persentase, keliling dan luas bangun datar, serta aritmatika sosial. Oleh karena itu, variasi metode pembelajaran dibutuhkan untuk mengakomodasi beragam gaya belajar siswa dan memastikan pemahaman konsep yang optimal.

Berbagai Metode Pembelajaran Matematika Kelas 6 Semester 2

Berikut ini beberapa metode pembelajaran yang efektif untuk matematika kelas 6 semester 2, disertai kelebihan, kekurangan, dan tingkat kesulitan implementasinya.

• Metode Penemuan: Siswa diajak untuk menemukan sendiri konsep melalui proses eksplorasi dan pemecahan masalah.
  • Kelebihan: Meningkatkan kemampuan berpikir kritis dan pemecahan masalah siswa, pemahaman konsep lebih mendalam dan bermakna.
  • Kekurangan: Membutuhkan waktu yang lebih lama, siswa yang kurang aktif mungkin kesulitan mengikuti proses penemuan.
  • Tingkat Kesulitan Implementasi: Sedang
• Metode Pembelajaran Kooperatif (Think-Pair-Share): Siswa berdiskusi dalam kelompok kecil untuk menyelesaikan masalah, kemudian berbagi hasil dengan kelas.
  • Kelebihan: Meningkatkan kemampuan kolaborasi dan komunikasi siswa, memberikan kesempatan bagi siswa untuk saling membantu.
  • Kekurangan: Membutuhkan pengelolaan kelas yang baik, siswa yang dominan mungkin menguasai diskusi.
  • Tingkat Kesulitan Implementasi: Mudah
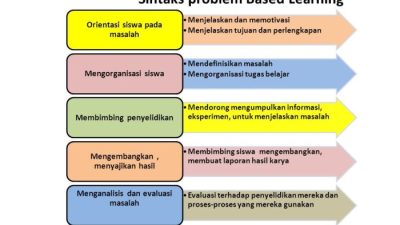
• Metode Pembelajaran Berbasis Masalah (PBL): Siswa diajak untuk memecahkan masalah kontekstual yang relevan dengan kehidupan sehari-hari.
  • Kelebihan: Meningkatkan kemampuan berpikir kritis dan pemecahan masalah siswa dalam konteks nyata, meningkatkan motivasi belajar.
  • Kekurangan: Membutuhkan perencanaan yang matang dan pemilihan masalah yang tepat, bisa memakan waktu yang cukup lama.
  • Tingkat Kesulitan Implementasi: Sulit
• Metode Demonstrasi: Guru mendemonstrasikan konsep dan prosedur secara langsung kepada siswa.
  • Kelebihan: Efisien untuk menjelaskan konsep yang kompleks, mudah dipahami oleh siswa.
  • Kekurangan: Kurang melibatkan siswa secara aktif, siswa mungkin hanya menerima informasi tanpa memahami konsep secara mendalam.
  • Tingkat Kesulitan Implementasi: Mudah
• Metode Ceramah: Guru menyampaikan materi secara verbal kepada siswa.
  • Kelebihan: Efisien untuk menyampaikan informasi dalam jumlah besar, mudah diimplementasikan.
  • Kekurangan: Kurang interaktif, siswa mungkin merasa bosan dan kurang terlibat.
  • Tingkat Kesulitan Implementasi: Mudah

Contoh Kegiatan Pembelajaran Metode Penemuan: Perbandingan dan Skala

Materi perbandingan dan skala dapat dipelajari dengan metode penemuan melalui serangkaian kegiatan yang dirancang untuk mengarahkan siswa menemukan sendiri konsep perbandingan dan skala.

1. Pertanyaan Pemantik: “Bagaimana kita dapat memperkecil atau memperbesar gambar atau objek agar tetap proporsional?”
2. Langkah-langkah Kegiatan Siswa:
   1. Siswa diberikan beberapa gambar dengan ukuran berbeda (misalnya, peta dan gambar aslinya).
   2. Siswa diminta untuk membandingkan ukuran gambar dan mengidentifikasi hubungan antara ukuran gambar dan ukuran aslinya.
   3. Siswa diminta untuk menghitung perbandingan ukuran gambar dan ukuran aslinya.
   4. Siswa diperkenalkan dengan konsep skala dan bagaimana cara menghitung skala.
   5. Siswa mengerjakan soal latihan yang berkaitan dengan perbandingan dan skala.
3. Penilaian: Penilaian dilakukan melalui observasi aktivitas siswa selama kegiatan, dan hasil pekerjaan siswa dalam mengerjakan soal latihan.

Penerapan Metode Pembelajaran Kooperatif Tipe Think-Pair-Share: Pengukuran Sudut

Metode Think-Pair-Share dapat diterapkan dalam pembelajaran pengukuran sudut dengan langkah-langkah berikut.

1. Think (Berpikir): Guru memberikan soal pengukuran sudut kepada siswa secara individual. Contoh soal: “ukurlah sudut pada gambar berikut!” ( disertai gambar sudut). Siswa diberikan waktu untuk berpikir dan mencoba menyelesaikan soal tersebut secara mandiri.
2. Pair (Berpasangan): Siswa berdiskusi dengan teman sebangku mereka untuk membahas jawaban dan strategi yang digunakan. Mereka saling membantu jika ada yang mengalami kesulitan.
3. Share (Berbagi): Setelah berdiskusi, setiap pasangan berbagi hasil diskusi mereka dengan kelas. Guru memfasilitasi diskusi kelas dan memberikan klarifikasi jika diperlukan. Kelompok dibentuk secara acak atau berdasarkan kemampuan yang beragam.
4. Penilaian: Penilaian dilakukan melalui observasi partisipasi siswa dalam diskusi dan ketepatan jawaban yang diberikan.

RPP Penggunaan Media Pembelajaran Berbasis Teknologi: Volume Kubus dan Balok

Berikut contoh RPP yang mengintegrasikan media pembelajaran berbasis teknologi (GeoGebra) untuk materi volume kubus dan balok.

• Tujuan Pembelajaran: Siswa mampu menghitung volume kubus dan balok.
• Materi Pembelajaran: Rumus volume kubus dan balok.
• Metode Pembelajaran: Pembelajaran berbasis teknologi dengan menggunakan GeoGebra.
• Media Pembelajaran: Aplikasi GeoGebra, laptop/komputer.
• Langkah-Langkah Pembelajaran (2 x 35 menit):
  1. Pendahuluan (10 menit): Guru menjelaskan konsep volume dan rumus volume kubus dan balok.
  2. Kegiatan Inti (50 menit): Siswa menggunakan GeoGebra untuk membuat model kubus dan balok, kemudian menghitung volumenya. Guru membimbing siswa dalam penggunaan GeoGebra.
  3. Penutup (15 menit): Guru memberikan soal latihan dan siswa mengerjakannya secara individu. Guru membahas jawaban bersama siswa.
• Penilaian: Penilaian dilakukan melalui observasi aktivitas siswa, hasil pekerjaan siswa dalam menggunakan GeoGebra, dan hasil pekerjaan siswa dalam mengerjakan soal latihan.

Perbandingan Metode Pembelajaran untuk Operasi Pecahan

Tabel berikut membandingkan beberapa metode pembelajaran yang efektif untuk materi pecahan, khususnya operasi penjumlahan dan pengurangan pecahan.

Nama Metode	Penjelasan Singkat Metode	Keunggulan	Kelemahan	Kesesuaian dengan Materi Pecahan
Metode Gambar	Menggunakan gambar untuk merepresentasikan pecahan dan operasi penjumlahan/pengurangan.	Mudah dipahami, visual.	Kurang efektif untuk pecahan dengan penyebut besar.	Sangat Sesuai
Metode Konkret	Menggunakan benda konkret (misal, potongan kertas) untuk merepresentasikan pecahan.	Membantu pemahaman konseptual.	Membutuhkan persiapan yang lebih matang.	Sangat Sesuai
Metode Algoritma	Menggunakan rumus dan prosedur standar untuk menghitung penjumlahan/pengurangan pecahan.	Efisien untuk perhitungan.	Kurang menekankan pemahaman konseptual.	Sesuai

Rekomendasi Strategi Diferensiasi Pembelajaran: Persentase

Strategi diferensiasi pembelajaran untuk materi persentase dapat meliputi: penyediaan berbagai tingkat kesulitan soal (soal mudah, sedang, dan sulit), penggunaan berbagai media pembelajaran (gambar, video, simulasi), dan penyesuaian waktu pengerjaan soal sesuai dengan kemampuan siswa. Guru dapat memberikan bimbingan individual kepada siswa yang membutuhkan bantuan tambahan.

Pertanyaan Evaluasi Pemahaman Siswa: Keliling dan Luas Bangun Datar

1. Berapakah keliling persegi panjang dengan panjang 10 cm dan lebar 5 cm? (Mudah)
2. Hitunglah luas segitiga dengan alas 8 cm dan tinggi 6 cm! (Sedang)
3. Sebuah taman berbentuk lingkaran dengan diameter 14 m. Berapakah keliling dan luas taman tersebut? (Sedang)
4. Bagaimana cara menghitung luas bangun datar tidak beraturan? Jelaskan dengan contoh! (Sulit)
5. Sebuah bangun datar memiliki keliling 24 cm dan luas 32 cm². Apakah mungkin bangun datar tersebut berbentuk persegi? Jelaskan alasanmu! (Sulit)

Flowchart Pembelajaran Berbasis Masalah (PBL): Aritmatika Sosial

Flowchart berikut menggambarkan alur pembelajaran berbasis masalah untuk materi aritmatika sosial.

(Karena keterbatasan format, flowchart tidak dapat ditampilkan dalam bentuk visual. Berikut deskripsi alur flowchart):

1. Presentasi Masalah: Guru menyajikan masalah kontekstual aritmatika sosial (misalnya, perhitungan untung rugi dalam berjualan).
2. Pemahaman Masalah: Siswa menganalisis masalah, mengidentifikasi informasi yang relevan, dan merumuskan pertanyaan.
3. Perencanaan Pemecahan Masalah: Siswa merencanakan strategi pemecahan masalah, termasuk menentukan rumus dan langkah-langkah yang diperlukan.
4. Pelaksanaan Rencana: Siswa mengerjakan masalah sesuai dengan rencana yang telah dibuat.
5. Evaluasi dan Refleksi: Siswa mengevaluasi hasil kerja mereka, merefleksikan proses pemecahan masalah, dan mengidentifikasi hal-hal yang perlu diperbaiki.
6. Presentasi dan Diskusi: Siswa mempresentasikan hasil kerja mereka dan berdiskusi dengan teman sekelas.

Penilaian Matematika Kelas 6 Semester 2

Penilaian yang komprehensif sangat penting untuk memastikan pemahaman siswa terhadap materi matematika kelas 6 semester 2. Penilaian tidak hanya berfokus pada hasil akhir, tetapi juga proses pembelajaran dan pemahaman konsep. Berikut ini beberapa contoh instrumen penilaian yang dapat digunakan untuk mengukur pemahaman siswa pada berbagai materi.

Contoh Instrumen Penilaian Pemahaman Konsep Bangun Ruang

Untuk mengukur pemahaman konsep bangun ruang, dapat digunakan berbagai metode penilaian, termasuk tes tertulis, praktikum, dan portofolio. Tes tertulis dapat berupa soal pilihan ganda, isian singkat, dan uraian. Praktikum dapat berupa kegiatan membuat model bangun ruang dan mengukur luas permukaan dan volumenya. Portofolio dapat berupa kumpulan karya siswa yang menunjukkan pemahaman mereka tentang bangun ruang.

Contoh soal uraian: Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 8 cm. Hitunglah volume balok tersebut! Jelaskan langkah-langkah perhitungannya!

Contoh soal pilihan ganda: Bangun ruang yang memiliki 6 sisi berbentuk persegi adalah…

• Kubus
• Balok
• Prisma segitiga
• Limas segitiga

Rubrik Penilaian Portofolio Proyek Matematika Terkait Pengukuran

Portofolio proyek matematika terkait pengukuran dapat dinilai menggunakan rubrik yang memperhatikan aspek-aspek seperti ketepatan pengukuran, kejelasan penyajian data, dan pemahaman konsep. Rubrik ini akan memberikan pedoman yang jelas dan objektif dalam menilai karya siswa.

Kriteria	Baik Sekali (4)	Baik (3)	Cukup (2)	Kurang (1)
Ketepatan Pengukuran	Pengukuran sangat tepat dan akurat.	Pengukuran tepat, dengan sedikit kesalahan yang tidak signifikan.	Pengukuran cukup tepat, tetapi terdapat beberapa kesalahan.	Pengukuran tidak tepat dan terdapat banyak kesalahan.
Kejelasan Penyajian Data	Data disajikan dengan sangat jelas, terorganisir, dan mudah dipahami.	Data disajikan dengan jelas dan mudah dipahami.	Data disajikan dengan cukup jelas, tetapi kurang terorganisir.	Data disajikan dengan kurang jelas dan sulit dipahami.
Pemahaman Konsep	Menunjukkan pemahaman konsep yang sangat baik dan mampu menerapkannya dengan tepat.	Menunjukkan pemahaman konsep yang baik dan mampu menerapkannya.	Menunjukkan pemahaman konsep yang cukup, tetapi masih terdapat beberapa kesalahan dalam penerapannya.	Menunjukkan pemahaman konsep yang kurang dan kesulitan dalam penerapannya.

Jenis Penilaian untuk Materi Persamaan dan Pertidaksamaan Linear Satu Variabel

Penilaian untuk materi persamaan dan pertidaksamaan linear satu variabel dapat dilakukan melalui berbagai metode, seperti tes tertulis, pemecahan masalah kontekstual, dan presentasi. Tes tertulis dapat berupa soal pilihan ganda, isian singkat, dan uraian. Pemecahan masalah kontekstual akan menguji kemampuan siswa dalam menerapkan konsep persamaan dan pertidaksamaan dalam situasi nyata. Presentasi dapat berupa penyelesaian soal di depan kelas.

Contoh soal pemecahan masalah: Umur Ani dua kali umur Budi. Jumlah umur mereka adalah 21 tahun. Berapakah umur Ani dan Budi?

Contoh Soal Ulangan Harian Matematika Kelas 6 Semester 2

Soal ulangan harian dirancang untuk mengukur pemahaman siswa terhadap materi yang telah dipelajari. Soal-soal harus bervariasi dan mencakup berbagai tingkat kesulitan.

1. Hitunglah luas lingkaran dengan diameter 14 cm!
2. Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Hitunglah kelilingnya!
3. Selesaikan persamaan: 2x + 5 = 11
4. Gambarlah sebuah kubus dan sebutkan bagian-bagiannya!

Kisi-Kisi Soal Ujian Tengah Semester Matematika Kelas 6 Semester 2

Kisi-kisi soal ujian tengah semester merupakan panduan dalam menyusun soal ujian. Kisi-kisi ini harus mencakup semua kompetensi dasar yang telah dipelajari pada semester 2.

Kompetensi Dasar	Indikator	Jumlah Soal	Jenis Soal
Menghitung luas dan keliling bangun datar	Menghitung luas persegi, persegi panjang, segitiga, dan lingkaran	5	Pilihan ganda dan uraian
Menghitung volume bangun ruang	Menghitung volume kubus dan balok	3	Uraian
Memecahkan masalah yang berkaitan dengan persamaan dan pertidaksamaan linear satu variabel	Menyelesaikan persamaan linear satu variabel	4	Pilihan ganda dan uraian

Alokasi Waktu dan Sumber Belajar Matematika Kelas 6 Semester 2

Perencanaan yang matang dalam alokasi waktu dan pemilihan sumber belajar sangat krusial untuk keberhasilan pembelajaran Matematika kelas 6 semester 2. Pemahaman yang mendalam terhadap materi, khususnya materi yang dianggap lebih sulit, memerlukan strategi pembelajaran yang efektif dan penggunaan sumber belajar yang beragam. Berikut ini uraian detail mengenai alokasi waktu, sumber belajar, dan strategi pembelajaran yang dapat diterapkan.

Alokasi Waktu Per Materi

Tabel berikut menunjukkan alokasi waktu yang direkomendasikan untuk setiap sub bab Matematika kelas 6 semester 2. Prioritas diberikan pada sub bab yang umumnya dianggap lebih menantang bagi siswa, seperti bangun ruang dan perhitungan pecahan yang kompleks.

Nah, berbicara tentang RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018, kita perlu melihat bagaimana materi tersebut bisa dikaitkan dengan kemampuan berpikir kritis siswa. Menariknya, untuk mengukur kemampuan berpikir kritis tersebut, kita bisa melihat contoh soal-soal AKM, seperti yang bisa Anda temukan di soal akm kelas 4 , meski levelnya berbeda. Memahami pola soal AKM akan membantu kita menyusun RPP yang lebih efektif dan terarah, memastikan siswa tidak hanya menghafal rumus, tetapi juga mampu mengaplikasikannya dalam pemecahan masalah yang lebih kompleks, sehingga tujuan pembelajaran dalam RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018 dapat tercapai secara optimal.

Nama Sub Bab	Jumlah Jam Belajar yang Direkomendasikan	Jenis Aktivitas Belajar	Tanggal Pelaksanaan (Contoh)
Bangun Ruang (Kubus dan Balok)	8 Jam	Pembahasan materi, latihan soal, pembuatan model 3D	Minggu 1-2
Pecahan Desimal dan Persen	6 Jam	Pembahasan materi, latihan soal, permainan edukatif	Minggu 3-4
Operasi Hitung Pecahan	7 Jam	Pembahasan materi, latihan soal, diskusi kelompok	Minggu 5-6
Statistika (Data dan Grafik)	5 Jam	Pembahasan materi, analisis data nyata, presentasi	Minggu 7-8
Pengukuran (Keliling dan Luas)	6 Jam	Pembahasan materi, praktikum pengukuran, pemecahan masalah	Minggu 9-10

Catatan: Tabel ini merupakan contoh dan dapat disesuaikan dengan kebutuhan dan kondisi belajar siswa.

Daftar Sumber Belajar Relevan

Sumber belajar yang beragam akan memperkaya pemahaman siswa. Berikut daftar sumber belajar yang dikategorikan berdasarkan tingkat kesulitan:

• Mudah: Buku teks pelajaran Matematika kelas 6 (sesuaikan dengan penerbit yang digunakan), beberapa website edukatif seperti (contoh: ruangguru.com, quipper.com – Catatan: URL ini hanya contoh, gunakan URL yang relevan dan aktif).
• Sedang: Buku referensi Matematika kelas 6 (sebutkan judul dan penulis jika memungkinkan), video pembelajaran YouTube yang menjelaskan konsep dasar (contoh: cari video dengan “Matematika kelas 6 bangun ruang”
  – Catatan: gunakan yang relevan dan periksa kualitas video sebelum direkomendasikan).
• Sulit: Buku latihan soal Matematika kelas 6 tingkat olimpiade (sebutkan judul dan penulis jika memungkinkan), website edukatif yang menyediakan soal-soal tantangan (contoh: website olimpiade matematika – Catatan: cari dan verifikasi website yang terpercaya dan relevan).

Rencana Penggunaan Media Pembelajaran untuk Bangun Ruang

Media pembelajaran yang tepat akan meningkatkan pemahaman siswa terhadap bangun ruang. Berikut rencana penggunaan media untuk materi bangun ruang:

1. Kubus dan balok nyata: Siswa dapat mengamati, memegang, dan menghitung sisi, rusuk, dan titik sudut secara langsung. Ini membantu visualisasi dan pemahaman konsep dasar.
2. Model 3D digital: Software atau aplikasi yang memungkinkan rotasi dan manipulasi model 3D bangun ruang akan membantu siswa memahami bangun ruang dari berbagai sudut pandang.
3. Presentasi PowerPoint: Presentasi dapat digunakan untuk menjelaskan definisi, rumus, dan contoh soal secara sistematis dan visual.

Sumber Daya yang Dibutuhkan

Pembelajaran Matematika kelas 6 semester 2 membutuhkan berbagai sumber daya untuk mendukung proses belajar mengajar yang efektif. Berikut daftar sumber daya yang dibutuhkan:

• Buku teks Matematika kelas 6
• Buku referensi dan buku latihan soal
• Alat tulis (pensil, penghapus, penggaris, jangka)
• Kubus dan balok untuk demonstrasi
• Komputer/laptop dan internet (untuk akses sumber belajar online)
• Proyektor dan layar (untuk presentasi)

Tabel Sumber Belajar Online dan Offline

Nama Sumber Belajar	Jenis Sumber Belajar	Deskripsi Singkat	Link (jika online)	Tingkat Kesulitan
Buku Teks Matematika Kelas 6 (Contoh: Erlangga)	Buku	Buku teks utama untuk pembelajaran	–	Sedang
Website Ruangguru	Website	Berisi materi, video pembelajaran, dan latihan soal	ruangguru.com (Contoh)	Sedang – Sulit
Video Pembelajaran YouTube (Contoh: Bangun Ruang Kubus dan Balok)	Video	Penjelasan konsep bangun ruang	(Contoh Link YouTube)	Mudah – Sedang
Buku Latihan Soal Olimpiade Matematika	Buku	Soal-soal tantangan untuk siswa berprestasi	–	Sulit

Contoh Soal dan Pembahasan (Bangun Ruang)

Berikut contoh soal dan pembahasan untuk materi bangun ruang (hanya contoh untuk satu sub bab):

1. Soal Mudah: Sebuah kubus memiliki panjang rusuk 5 cm. Berapa volume kubus tersebut?
2. Pembahasan Mudah: Volume kubus = s ³ = 5 ³ = 125 cm ³
3. Soal Sedang: Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Berapa luas permukaan balok tersebut?
4. Pembahasan Sedang: Luas permukaan balok = 2(panjang x lebar + panjang x tinggi + lebar x tinggi) = 2(10×5 + 10×3 + 5×3) = 2(50 + 30 + 15) = 190 cm ²
5. Soal Sulit: Sebuah kotak berbentuk kubus memiliki volume 216 cm ³. Berapa panjang diagonal ruang kubus tersebut?
6. Pembahasan Sulit: Panjang rusuk kubus = akar pangkat tiga dari 216 = 6 cm. Panjang diagonal ruang = rusuk x akar pangkat tiga dari 3 = 6 x akar pangkat tiga dari 3 ≈ 10.39 cm

Catatan: Contoh soal dan pembahasan lainnya untuk sub bab lain dapat ditambahkan.

Strategi Mengatasi Kesulitan Belajar

Beberapa strategi dapat diterapkan untuk mengatasi kesulitan belajar siswa, seperti:

• Pembelajaran remedial: Memberikan bimbingan tambahan kepada siswa yang mengalami kesulitan.
• Metode pembelajaran yang bervariasi: Menggunakan berbagai metode pembelajaran seperti diskusi kelompok, permainan edukatif, dan proyek untuk meningkatkan pemahaman.
• Penggunaan media pembelajaran yang beragam: Menggunakan media pembelajaran yang sesuai dengan gaya belajar siswa.
• Kerja sama dengan orang tua: Membangun komunikasi yang baik dengan orang tua untuk memantau perkembangan belajar siswa.

Relevansi dengan Kehidupan Sehari-hari

Matematika, khususnya materi yang dipelajari di kelas 6 semester 2, bukan sekadar angka dan rumus abstrak. Konsep-konsep tersebut memiliki aplikasi luas dalam kehidupan sehari-hari, membantu kita dalam pengambilan keputusan dan pemecahan masalah praktis. Wawancara mendalam berikut ini akan mengungkap bagaimana materi pecahan, persentase, bangun ruang, dan persamaan/pertidaksamaan linear satu variabel terintegrasi dalam aktivitas kita sehari-hari.

Penerapan Konsep Pecahan dalam Kehidupan Sehari-hari

Pecahan merupakan fondasi dalam memahami bagian-bagian dari keseluruhan. Bayangkan Anda membagi sebuah pizza menjadi 8 potong. Jika Anda memakan 3 potong, maka Anda telah memakan 3/8 bagian pizza. Konsep ini juga berlaku dalam berbagai situasi lain, seperti membagi kue, menghitung waktu (misalnya, ½ jam = 30 menit), atau membagi tugas kelompok. Memahami pecahan memudahkan kita dalam membagi sesuatu secara adil dan proporsional.

Penggunaan Persentase dalam Situasi Riil

Persentase sering digunakan untuk mewakili bagian dari keseluruhan dalam bentuk perbandingan terhadap seratus. Contohnya, diskon 20% pada sebuah barang berarti Anda hanya membayar 80% dari harga aslinya. Persentase juga digunakan dalam laporan keuangan, statistik, dan bahkan dalam menghitung nilai ujian. Kemampuan memahami dan menghitung persentase sangat penting untuk menganalisis informasi dan membuat keputusan keuangan yang bijak.

Misalnya, memahami persentase kenaikan harga BBM atau menghitung persentase keuntungan dari suatu usaha.

Pentingnya Mempelajari Bangun Ruang dalam Kehidupan Sehari-hari

Bangun ruang hadir di sekitar kita. Rumah kita, kotak kado, kaleng minuman, semuanya merupakan contoh bangun ruang. Mempelajari bangun ruang membantu kita memahami volume dan luas permukaan berbagai objek. Kemampuan ini sangat berguna dalam berbagai hal, seperti menghitung jumlah cat yang dibutuhkan untuk mengecat dinding, menentukan kapasitas sebuah tangki air, atau mendesain kemasan produk. Contohnya, dalam mendesain sebuah akuarium, kita perlu menghitung volume air yang dibutuhkan agar ikan dapat hidup dengan nyaman.

Contoh Kasus Penggunaan Persamaan dan Pertidaksamaan Linear Satu Variabel

Persamaan dan pertidaksamaan linear satu variabel digunakan untuk memodelkan dan menyelesaikan masalah yang melibatkan satu variabel. Contohnya, jika Andi membeli 2 buku tulis dan 1 pensil dengan total harga Rp 15.000, dan harga pensil adalah Rp 3.000, maka kita dapat membuat persamaan linear untuk mencari harga satu buku tulis: 2x + 3000 = 15000, di mana x mewakili harga satu buku tulis.

Pertidaksamaan linear, misalnya, dapat digunakan untuk menentukan batas minimal atau maksimal suatu variabel. Misalnya, seorang petani harus memanen minimal 100 kg padi untuk memenuhi kebutuhan keluarganya.

Ilustrasi Situasi Kehidupan Sehari-hari yang Membutuhkan Kemampuan Menghitung Volume Bangun Ruang

Bayangkan Anda ingin membuat sebuah kolam renang kecil di halaman rumah. Untuk menentukan jumlah air yang dibutuhkan, Anda perlu menghitung volume kolam renang tersebut. Jika kolam tersebut berbentuk balok dengan panjang 3 meter, lebar 2 meter, dan kedalaman 1 meter, maka volumenya adalah 6 meter kubik (3 x 2 x 1 = 6). Contoh lain adalah menghitung volume tanah yang dibutuhkan untuk membuat sebuah taman atau menghitung volume pasir yang dibutuhkan untuk membuat pondasi bangunan.

Kemampuan menghitung volume bangun ruang sangat penting dalam berbagai proyek konstruksi dan desain.

Diferensiasi Pembelajaran

Diferensiasi pembelajaran merupakan kunci keberhasilan dalam mendidik siswa kelas 6, khususnya dalam mata pelajaran matematika. Dengan mempertimbangkan beragam kemampuan, gaya belajar, dan kebutuhan khusus siswa, guru dapat menciptakan lingkungan belajar yang inklusif dan efektif. Wawancara berikut ini akan mengulas strategi diferensiasi pembelajaran yang dapat diterapkan dalam RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018.

Modifikasi Pembelajaran untuk Siswa Berkebutuhan Khusus

Modifikasi pembelajaran bagi siswa berkebutuhan khusus bertujuan untuk memberikan akses yang sama terhadap materi pelajaran. Hal ini dapat dilakukan melalui berbagai cara, disesuaikan dengan jenis kebutuhan khusus yang dimiliki siswa.

• Siswa dengan kesulitan belajar: Penyederhanaan soal, penggunaan media visual yang lebih banyak, dan pembagian tugas menjadi bagian-bagian kecil dapat membantu mereka memahami materi dengan lebih baik. Contohnya, untuk siswa dengan disleksia, soal cerita dapat diubah menjadi soal hitung langsung dengan mengurangi jumlah kata dan kalimat yang rumit.
• Siswa dengan gangguan pendengaran: Penggunaan media visual seperti video dengan teks, demonstrasi langsung, dan penerjemah isyarat dapat membantu mereka mengikuti pelajaran. Materi dapat juga disampaikan secara tertulis dengan bahasa yang sederhana dan mudah dipahami.
• Siswa dengan gangguan penglihatan: Penggunaan huruf besar, buku braille, atau software pembaca layar dapat membantu mereka mengakses materi pelajaran. Guru juga dapat memberikan penjelasan verbal yang detail.

Strategi Pembelajaran yang Mengakomodasi Berbagai Gaya Belajar

Siswa memiliki gaya belajar yang berbeda-beda, ada yang visual, auditori, kinestetik, dan kombinasi ketiganya. Strategi pembelajaran yang beragam akan memastikan semua siswa dapat menyerap materi dengan optimal.

• Visual: Penggunaan diagram, grafik, peta pikiran, dan video edukatif dapat membantu siswa visual memahami konsep matematika.
• Auditori: Diskusi kelompok, presentasi, dan penjelasan verbal dari guru akan efektif bagi siswa auditori. Penjelasan konsep dengan menggunakan analogi dan cerita juga dapat membantu.
• Kinestetik: Aktivitas manipulatif seperti menggunakan benda konkret, permainan edukatif, dan simulasi akan membantu siswa kinestetik dalam memahami konsep matematika. Contohnya, menggunakan balok untuk memahami pecahan atau menggunakan uang mainan untuk mempelajari operasi hitung.

Penyesuaian Tingkat Kesulitan Soal untuk Siswa dengan Kemampuan Berbeda

Menyesuaikan tingkat kesulitan soal sangat penting untuk memastikan semua siswa dapat tertantang dan merasa berhasil. Ini dapat dilakukan dengan menyediakan soal pada berbagai tingkat kesulitan.

Tingkat Kesulitan	Contoh Soal
Mudah	2 + 3 = ?
Sedang	Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Berapa luas persegi panjang tersebut?
Sulit	Ani memiliki pita sepanjang 1,5 meter. Ia menggunakan 2/5 bagian untuk membuat bunga. Berapa sisa pita Ani?

Kegiatan Pembelajaran yang Mengajak Siswa Aktif dan Berpartisipasi, Rpp matematika kelas 6 semester 2 kurikulum 2013 revisi 2018

Pembelajaran yang aktif dan partisipatif akan meningkatkan pemahaman dan minat siswa terhadap matematika. Beberapa kegiatan yang dapat dilakukan antara lain:

• Diskusi kelompok
• Presentasi hasil kerja
• Game edukatif
• Proyek kelompok
• Pertanyaan dan jawaban interaktif

Contoh Tugas Tambahan untuk Siswa yang Telah Menguasai Materi

Untuk siswa yang telah menguasai materi, perlu diberikan tugas tambahan untuk menantang kemampuan mereka dan memperluas pemahaman mereka.

• Soal olimpiade matematika
• Mencari informasi tambahan tentang topik yang dibahas
• Membuat soal sendiri
• Membuat presentasi tentang konsep matematika tertentu
• Membantu teman sebaya yang masih kesulitan

Integrasi Nilai-Nilai Karakter

Integrasi nilai-nilai karakter dalam pembelajaran Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018 bukan sekadar pelengkap, melainkan kunci untuk membentuk siswa yang tidak hanya cerdas secara akademik, tetapi juga berkarakter mulia. Proses pembelajaran matematika dapat dirancang sedemikian rupa sehingga secara simultan menanamkan nilai-nilai positif, membangun pribadi siswa yang utuh dan siap menghadapi tantangan masa depan.

Nilai-Nilai Karakter dalam Pembelajaran Matematika

Beberapa nilai karakter yang relevan dan dapat diintegrasikan dalam pembelajaran Matematika Kelas 6 Semester 2 antara lain jujur, tanggung jawab, kerja sama, disiplin, percaya diri, dan tekun. Pemilihan nilai karakter ini didasarkan pada relevansinya dengan proses pembelajaran matematika dan pembentukan karakter siswa yang holistik.

Contoh Kegiatan Pembelajaran yang Menanamkan Nilai Jujur dan Tanggung Jawab

Untuk menanamkan nilai jujur, guru dapat menerapkan sistem penilaian diri dan saling menilai antar siswa dengan menekankan kejujuran dalam prosesnya. Misalnya, siswa diminta untuk mengevaluasi pemahaman mereka sendiri terhadap materi yang telah dipelajari, kemudian membandingkannya dengan hasil kerja kelompok. Sedangkan untuk menanamkan tanggung jawab, siswa dapat diberikan tugas individu atau kelompok dengan tenggat waktu yang jelas. Kegagalan menyelesaikan tugas tepat waktu menjadi konsekuensi yang harus ditanggung siswa, sehingga mereka belajar bertanggung jawab atas tindakannya.

Contohnya, menyelesaikan proyek matematika berupa presentasi model bangun ruang, dimana setiap anggota kelompok bertanggung jawab atas bagiannya dan presentasi dilakukan secara kolaboratif.

Integrasi Nilai Kerja Sama dalam Pembelajaran Matematika

Pembelajaran matematika yang menekankan kerja sama dapat dilakukan melalui berbagai kegiatan kelompok. Contohnya, siswa dapat bekerja sama dalam memecahkan masalah matematika yang kompleks, mengerjakan proyek matematika, atau bermain game edukatif yang membutuhkan kolaborasi. Dalam proses kerja sama, siswa belajar untuk saling menghargai pendapat, berbagi ide, dan mencapai kesepakatan bersama. Guru berperan sebagai fasilitator, membimbing dan memastikan setiap anggota kelompok berkontribusi aktif.

Penilaian yang Memperhatikan Aspek Sikap dan Perilaku Siswa

Penilaian tidak hanya berfokus pada aspek kognitif (pengetahuan dan keterampilan), tetapi juga aspek afektif (sikap dan perilaku). Guru dapat menggunakan berbagai metode penilaian, seperti observasi, penilaian diri, penilaian antar teman, dan portofolio. Observasi dilakukan untuk melihat partisipasi siswa dalam kegiatan kelompok, sikap jujur dalam mengerjakan tugas, dan tanggung jawab dalam menyelesaikan pekerjaan. Penilaian diri dan antar teman memungkinkan siswa untuk mengevaluasi sikap dan perilaku mereka sendiri dan teman sekelompoknya.

Portofolio dapat digunakan untuk mengumpulkan bukti-bukti perkembangan sikap dan perilaku siswa selama proses pembelajaran.

Aktivitas Pembelajaran yang Menumbuhkan Rasa Percaya Diri

Untuk menumbuhkan rasa percaya diri, guru dapat memberikan kesempatan kepada siswa untuk menunjukkan kemampuan mereka. Contohnya, siswa dapat mempresentasikan hasil kerja mereka di depan kelas, berpartisipasi dalam kompetisi matematika, atau menjawab pertanyaan yang menantang. Dukungan dan apresiasi dari guru dan teman sebaya sangat penting untuk meningkatkan rasa percaya diri siswa. Memberikan umpan balik yang konstruktif dan positif, bukan hanya berfokus pada kesalahan, akan mendorong siswa untuk terus berkembang dan percaya pada kemampuannya.

Guru juga bisa menerapkan strategi pembelajaran diferensiasi, sehingga setiap siswa merasa tertantang dan mampu menunjukkan potensinya sesuai dengan kemampuan masing-masing.

Penggunaan Teknologi dalam Pembelajaran: Rpp Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018

Integrasi teknologi dalam pembelajaran Matematika kelas 6 semester 2 menawarkan potensi luar biasa untuk meningkatkan pemahaman konsep, meningkatkan keterlibatan siswa, dan memfasilitasi pembelajaran yang lebih personal. Dengan memanfaatkan berbagai perangkat lunak dan aplikasi edukatif, guru dapat menciptakan lingkungan belajar yang interaktif dan menyenangkan, sehingga siswa lebih mudah memahami konsep-konsep matematika yang seringkali dianggap rumit.

Manfaat Penggunaan Teknologi dalam Pembelajaran Matematika

Penggunaan teknologi dalam pembelajaran Matematika kelas 6 semester 2 memberikan sejumlah manfaat signifikan. Teknologi memungkinkan visualisasi konsep abstrak dengan lebih jelas, seperti geometri tiga dimensi atau manipulasi aljabar. Simulasi dan game edukatif dapat membuat pembelajaran lebih interaktif dan menyenangkan, meningkatkan motivasi dan pemahaman siswa. Selain itu, teknologi memungkinkan diferensiasi pembelajaran, sehingga guru dapat menyesuaikan kecepatan dan metode pembelajaran sesuai kebutuhan individu siswa.

Akses ke sumber daya online yang luas juga memperkaya materi pembelajaran dan memberikan kesempatan eksplorasi lebih lanjut bagi siswa yang ingin mempelajari lebih dalam.

Contoh Aplikasi dan Website Edukatif

Berbagai aplikasi dan website edukatif dapat mendukung pembelajaran Matematika. Sebagai contoh, aplikasi seperti Khan Academy menawarkan ribuan video pembelajaran dan latihan soal interaktif yang mencakup berbagai topik Matematika. GeoGebra merupakan perangkat lunak yang memungkinkan siswa untuk memvisualisasikan dan memanipulasi objek geometri, sementara aplikasi seperti Math Playground menyediakan game edukatif yang menyenangkan dan menantang untuk memperkuat pemahaman konsep Matematika.

Website-website seperti IXL Learning menyediakan latihan soal yang terstruktur dan adaptif, menyesuaikan tingkat kesulitan berdasarkan performa siswa.

Rencana Penggunaan Perangkat Lunak Matematika

Suatu rencana penggunaan perangkat lunak matematika yang efektif harus mempertimbangkan kebutuhan siswa dan tujuan pembelajaran. Misalnya, untuk topik geometri, GeoGebra dapat digunakan untuk membantu siswa memvisualisasikan bentuk-bentuk geometri, melakukan konstruksi geometri, dan menyelesaikan masalah geometri. Untuk topik pecahan, aplikasi interaktif yang memungkinkan siswa memanipulasi model visual pecahan dapat membantu mereka memahami konsep pecahan dengan lebih baik. Rencana tersebut harus mencakup kegiatan pendahuluan, kegiatan inti, dan kegiatan penutup yang terintegrasi dengan perangkat lunak, serta evaluasi pemahaman siswa setelah menggunakan perangkat lunak tersebut.

Penting untuk memastikan perangkat lunak tersebut mudah digunakan dan sesuai dengan kemampuan teknis siswa.

Aktivitas Pembelajaran yang Memanfaatkan Media Interaktif

Aktivitas pembelajaran yang memanfaatkan media interaktif dapat dirancang untuk meningkatkan keterlibatan dan pemahaman siswa. Contohnya, siswa dapat menggunakan aplikasi simulasi untuk menyelesaikan masalah cerita yang melibatkan konsep pecahan atau persentase. Mereka juga dapat berkolaborasi dalam proyek berbasis teknologi, seperti membuat presentasi interaktif tentang konsep geometri atau membuat game edukatif sederhana yang berkaitan dengan materi yang sedang dipelajari. Media interaktif seperti video pembelajaran, animasi, dan simulasi dapat digunakan untuk menjelaskan konsep-konsep yang kompleks dan sulit dipahami.

Guru dapat juga menggunakan platform online untuk memberikan tugas dan kuis, serta memantau kemajuan belajar siswa secara real-time.

RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018 memang menuntut kreativitas guru dalam penyusunannya. Kita perlu memastikan materi terintegrasi dengan baik, dan untuk mendukung hal tersebut, platform seperti iyes bisa menjadi solusi untuk mengakses berbagai sumber belajar. Dengan referensi yang memadai, kita dapat mengembangkan RPP yang lebih inovatif dan sesuai dengan kebutuhan siswa, menjadikan proses pembelajaran matematika lebih efektif dan menyenangkan.

Perbandingan Beberapa Aplikasi Pembelajaran Matematika

Aplikasi	Fitur Utama	Kelebihan	Kekurangan
Khan Academy	Video pembelajaran, latihan soal, materi terstruktur	Gratis, konten yang luas, adaptif	Antarmuka mungkin kurang menarik bagi sebagian siswa
GeoGebra	Visualisasi geometri, konstruksi geometri, simulasi	Interaktif, visual, fleksibel	Kurva pembelajaran yang agak curam bagi pengguna pemula
IXL Learning	Latihan soal adaptif, pelaporan kemajuan	Terstruktur, adaptif, pelaporan yang detail	Berbayar, mungkin kurang menekankan pemahaman konsep
Math Playground	Game edukatif, aktivitas interaktif	Menyenangkan, meningkatkan motivasi	Konten mungkin kurang komprehensif

Evaluasi dan Refleksi Pembelajaran

Evaluasi dan refleksi merupakan komponen penting dalam siklus pembelajaran yang efektif. Proses ini memungkinkan guru untuk mengidentifikasi kekuatan dan kelemahan dalam pengajaran mereka, serta untuk menyesuaikan strategi pembelajaran agar lebih sesuai dengan kebutuhan siswa. Artikel ini akan membahas berbagai aspek evaluasi dan refleksi pembelajaran, khususnya dalam konteks pembelajaran tematik kelas 4 SD tema “Perubahan Cuaca”, dengan penekanan pada penggunaan instrumen evaluasi diri, model refleksi Schön, dan revisi RPP.

Instrumen Evaluasi Diri Guru

Berikut contoh instrumen evaluasi diri untuk guru setelah melaksanakan pembelajaran tematik kelas 4 SD tema “Perubahan Cuaca”, menggunakan skala Likert 5 pilihan jawaban (Sangat Baik, Baik, Cukup, Kurang, Sangat Kurang):

1. Persiapan materi pembelajaran sudah terencana dengan baik dan lengkap.
2. Media pembelajaran yang digunakan menarik dan relevan dengan materi.
3. Metode pembelajaran yang diterapkan efektif dan sesuai dengan karakteristik siswa.
4. Alokasi waktu untuk setiap kegiatan pembelajaran terdistribusi dengan baik.
5. Saya mampu mengelola kelas dengan efektif dan menciptakan suasana belajar yang kondusif.
6. Saya mampu memberikan umpan balik yang konstruktif kepada siswa.
7. Siswa aktif berpartisipasi dalam kegiatan pembelajaran.
8. Tujuan pembelajaran tercapai sesuai dengan indikator yang telah ditetapkan.
9. Saya mampu mengakomodasi perbedaan gaya belajar siswa.
10. Saya mampu melakukan asesmen terhadap pemahaman siswa secara efektif.

Langkah-langkah Refleksi Pembelajaran (Model Schön)

Model refleksi Schön menekankan pada proses berpikir reflektif yang sistematis. Berikut langkah-langkahnya:

1. Deskripsi Pengalaman: Guru mendeskripsikan pengalaman mengajar secara detail, termasuk apa yang terjadi selama pembelajaran, interaksi dengan siswa, dan tantangan yang dihadapi. Contoh: “Pada sesi pembelajaran tentang siklus air, sebagian besar siswa kesulitan memahami konsep evaporasi. Mereka tampak kurang fokus dan banyak yang bercakap-cakap.”
2. Analisis Pengalaman: Guru menganalisis pengalaman tersebut, mencari pola, dan mengidentifikasi faktor-faktor yang berkontribusi pada keberhasilan atau kegagalan pembelajaran. Contoh: “Kesulitan siswa memahami evaporasi mungkin disebabkan oleh kurangnya media visual yang menarik dan penjelasan yang kurang terstruktur.”
3. Evaluasi Pengalaman: Guru mengevaluasi efektivitas strategi pembelajaran yang digunakan dan dampaknya terhadap pencapaian tujuan pembelajaran. Contoh: “Strategi pembelajaran yang saya gunakan kurang efektif karena tidak mampu mengakomodasi gaya belajar siswa yang beragam.”
4. Perencanaan Tindakan Selanjutnya: Guru merencanakan tindakan perbaikan untuk pembelajaran di masa mendatang berdasarkan evaluasi yang dilakukan. Contoh: “Pada pembelajaran selanjutnya, saya akan menggunakan video animasi siklus air dan memberikan kesempatan bagi siswa untuk melakukan eksperimen sederhana terkait evaporasi.”

Penggunaan Hasil Evaluasi untuk Perbaikan Pembelajaran

Hasil evaluasi diri, baik kuantitatif (misalnya, skor rata-rata dari instrumen evaluasi) maupun kualitatif (misalnya, catatan anekdot tentang interaksi siswa), digunakan untuk mengidentifikasi area yang perlu diperbaiki. Data kuantitatif menunjukkan gambaran umum, sementara data kualitatif memberikan wawasan yang lebih mendalam. Misalnya, skor rendah pada butir pertanyaan tentang “media pembelajaran” menunjukkan perlunya revisi RPP untuk memasukkan media yang lebih menarik dan interaktif, seperti video atau simulasi.

Nah, RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018 memang membutuhkan perencanaan yang matang. Kita perlu memastikan setiap materi tersampaikan dengan efektif. Menariknya, untuk mendapatkan inspirasi penyusunan RPP yang lebih holistik, kita bisa melihat contoh-contoh RPP lainnya, misalnya dengan melihat referensi contoh rpp tematik kelas 5 yang bisa memberikan gambaran bagaimana menggabungkan beberapa mata pelajaran.

Dari situ, kita bisa memperoleh ide-ide kreatif untuk mengembangkan RPP Matematika kelas 6 kita agar lebih menarik dan mudah dipahami siswa. Kembali ke RPP Matematika kelas 6, pengembangan soal dan metode pembelajaran yang tepat menjadi kunci keberhasilannya.

Kelebihan dan Kekurangan Pembelajaran

Tabel berikut mencatat kelebihan dan kekurangan dalam pelaksanaan pembelajaran tematik kelas 4 SD tema “Perubahan Cuaca”:

Aspek Pembelajaran	Kelebihan	Kekurangan	Akar Masalah	Rencana Perbaikan
Persiapan	Materi sudah disusun secara sistematis	Media pembelajaran kurang variatif	Keterbatasan sumber daya	Menggunakan media digital dan memanfaatkan sumber daya alam sekitar
Pelaksanaan	Siswa antusias dalam diskusi kelompok	Waktu kurang cukup untuk kegiatan praktik	Perencanaan alokasi waktu yang kurang tepat	Menyesuaikan alokasi waktu dan merampingkan beberapa kegiatan
Ketercapaian Tujuan	Sebagian besar siswa mencapai KKM	Beberapa siswa masih kesulitan memahami konsep cuaca ekstrem	Penjelasan konsep yang kurang detail	Menambahkan contoh konkret dan visualisasi yang lebih jelas
Persiapan	Lembar kerja terdistribusi dengan baik	Lembar kerja kurang menantang	Kurangnya variasi tingkat kesulitan soal	Membuat soal dengan tingkat kesulitan yang bervariasi
Pelaksanaan	Diskusi kelas berjalan lancar	Beberapa siswa mendominasi diskusi	Kurangnya strategi untuk melibatkan semua siswa	Menerapkan teknik pembelajaran kooperatif yang lebih efektif

Langkah-Langkah Revisi RPP

Revisi RPP didasarkan pada temuan evaluasi. Langkah-langkahnya meliputi:

1. Analisis Hasil Evaluasi: Tinjau kembali data kuantitatif dan kualitatif dari instrumen evaluasi dan tabel kelebihan/kekurangan.
2. Revisi Tujuan Pembelajaran: Sesuaikan tujuan pembelajaran jika perlu, berdasarkan ketercapaian tujuan yang belum optimal. Contoh: Jika siswa kesulitan memahami konsep cuaca ekstrem, tujuan pembelajaran perlu dirumuskan ulang agar lebih spesifik dan terukur.
3. Revisi Metode Pembelajaran: Ganti atau modifikasi metode pembelajaran yang kurang efektif. Contoh: Jika diskusi kelas didominasi beberapa siswa, gunakan metode pembelajaran kooperatif untuk memastikan partisipasi semua siswa.
4. Revisi Media Pembelajaran: Tambahkan atau ganti media pembelajaran yang kurang menarik atau kurang relevan. Contoh: Gunakan video animasi atau simulasi untuk menjelaskan konsep yang sulit dipahami.
5. Revisi Penilaian: Sesuaikan instrumen penilaian agar lebih sesuai dengan tujuan pembelajaran dan kebutuhan siswa. Contoh: Jika beberapa siswa masih kesulitan memahami konsep cuaca ekstrem, tambahkan soal-soal yang lebih sederhana dan berfokus pada konsep dasar.

Diagram Alur Evaluasi dan Refleksi Pembelajaran

Diagram alur (flowchart) akan menggambarkan proses evaluasi dan refleksi pembelajaran secara visual, dimulai dari pelaksanaan pembelajaran hingga revisi RPP. Proses ini dimulai dengan pelaksanaan pembelajaran, diikuti dengan pengumpulan data melalui instrumen evaluasi dan observasi. Data kemudian dianalisis untuk mengidentifikasi kelebihan dan kekurangan pembelajaran. Berdasarkan analisis tersebut, guru melakukan refleksi menggunakan model Schön dan merevisi RPP untuk pembelajaran selanjutnya.

Proses ini bersifat siklis, di mana evaluasi dan refleksi dilakukan secara berkelanjutan untuk meningkatkan kualitas pembelajaran.

Pertanyaan Refleksi Kritis

Berikut tiga pertanyaan refleksi kritis yang dapat digunakan guru:

1. Bagaimana saya dapat lebih efektif mengakomodasi perbedaan gaya belajar dan kebutuhan siswa dalam pembelajaran?
2. Bagaimana strategi pembelajaran yang saya gunakan berdampak pada pemahaman konseptual dan keterampilan siswa?
3. Apa yang dapat saya lakukan untuk menciptakan lingkungan belajar yang lebih inklusif dan mendukung bagi semua siswa?

Perbedaan Evaluasi Formatif dan Sumatif

Evaluasi formatif dilakukan selama proses pembelajaran untuk memantau pemahaman siswa dan menyesuaikan strategi pembelajaran. Evaluasi sumatif dilakukan di akhir pembelajaran untuk mengukur pencapaian tujuan pembelajaran secara keseluruhan. Keduanya diintegrasikan dalam refleksi pembelajaran. Data dari evaluasi formatif membantu guru dalam melakukan penyesuaian selama proses pembelajaran, sementara data dari evaluasi sumatif digunakan untuk mengevaluasi efektivitas pembelajaran secara keseluruhan dan menginformasikan revisi RPP untuk siklus pembelajaran berikutnya.

Perencanaan Pembelajaran Berdiferensiasi

Perencanaan pembelajaran berdiferensiasi merupakan pendekatan yang mengakui keberagaman kemampuan dan gaya belajar siswa. Strategi ini dirancang untuk memenuhi kebutuhan individu, memastikan setiap siswa dapat mencapai potensi maksimalnya. Berikut ini contoh penerapannya dalam pembelajaran Matematika kelas 4 SD dengan tema “Pengukuran” selama satu minggu.

Contoh Rencana Pembelajaran Tematik Satu Minggu

Rencana pembelajaran ini mencakup pengukuran panjang, luas, volume, berat, dan waktu, dengan penyesuaian strategi untuk tiga level kemampuan siswa: tinggi, sedang, dan rendah. Indikator Pencapaian Kompetensi (IPK) dirumuskan secara terukur dan tercapai, memastikan setiap siswa memiliki target belajar yang jelas dan terukur.

• Hari 1: Pengukuran Panjang. IPK: Siswa mampu mengukur panjang benda menggunakan satuan baku (cm dan m) dan tak baku (jengkal, hasta).
• Hari 2: Pengukuran Luas. IPK: Siswa mampu menghitung luas bangun datar sederhana (persegi dan persegi panjang) menggunakan satuan baku (cm²).
• Hari 3: Pengukuran Volume. IPK: Siswa mampu mengukur volume benda cair menggunakan satuan baku (ml dan liter).
• Hari 4: Pengukuran Berat. IPK: Siswa mampu mengukur berat benda menggunakan satuan baku (gram dan kilogram).
• Hari 5: Pengukuran Waktu. IPK: Siswa mampu membaca dan menafsirkan waktu pada jam analog dan digital.

Penyesuaian Strategi Pembelajaran Berdasarkan Tingkat Kemampuan Siswa

Strategi pembelajaran, media pembelajaran, dan alokasi waktu disesuaikan dengan tingkat kemampuan siswa. Pembelajaran berbasis proyek diterapkan untuk siswa berkemampuan tinggi, pembelajaran kooperatif untuk siswa berkemampuan sedang, dan pembelajaran remedial individual untuk siswa berkemampuan rendah.

• Siswa Berkemampuan Tinggi: Menggunakan pendekatan inquiry-based learning, diberikan proyek penelitian sederhana, misalnya menghitung volume benda tidak beraturan dengan metode pencelupan. Mereka merancang percobaan, mengumpulkan dan menganalisis data, serta mempresentasikan temuan.
• Siswa Berkemampuan Sedang: Menggunakan pembelajaran kooperatif, berkolaborasi dalam kelompok untuk menyelesaikan soal-soal latihan dan diskusi. Media pembelajaran berupa kartu gambar dan balok satuan digunakan untuk mempermudah pemahaman konsep.
• Siswa Berkemampuan Rendah: Mendapatkan pembelajaran remedial individual dengan pendekatan yang lebih terstruktur dan bantuan konkret seperti balok satuan dan lembar kerja yang lebih sederhana. Soal latihan diberikan bertahap dengan tingkat kesulitan yang rendah.

Proyek Penelitian Sederhana untuk Siswa Berkemampuan Tinggi

Proyek penelitian ini berfokus pada pengukuran volume benda tidak beraturan. Siswa merancang percobaan, misalnya dengan metode pencelupan, mengumpulkan data volume air sebelum dan sesudah benda dimasukkan, menganalisis data untuk menentukan volume benda, dan mempresentasikan temuan mereka dalam bentuk laporan tertulis dan presentasi lisan. Kriteria penilaian meliputi rancangan percobaan, keakuratan pengukuran, analisis data, dan presentasi.

Dukungan Pembelajaran untuk Siswa yang Mengalami Kesulitan Belajar

Untuk siswa yang mengalami kesulitan dalam memahami konsep pengukuran luas dan keliling, diberikan dukungan melalui penggunaan media konkret seperti balok satuan, kartu gambar, dan lembar kerja terdiferensiasi. Contoh soal latihan yang terdiferensiasi diberikan, dimulai dari soal yang sederhana dan bertahap meningkat kesulitannya.

• Contoh Soal Latihan (Tingkat Rendah): Hitung luas persegi dengan sisi 5 cm.
• Contoh Soal Latihan (Tingkat Sedang): Hitung luas persegi panjang dengan panjang 10 cm dan lebar 5 cm.
• Contoh Soal Latihan (Tingkat Tinggi): Hitung luas bangun gabungan yang terdiri dari persegi dan persegi panjang.

Tabel Diferensiasi Pembelajaran

Subtema	IPK	Strategi Pembelajaran (Tinggi, Sedang, Rendah)	Media Pembelajaran (Tinggi, Sedang, Rendah)	Penilaian (Tinggi, Sedang, Rendah)	Alokasi Waktu (Tinggi, Sedang, Rendah)
Pengukuran Panjang	Mengukur panjang	Proyek, Kooperatif, Remedial	Penggaris, Meteran, Jengkal, Lembar Kerja	Laporan, Tes, Observasi	45 menit, 60 menit, 75 menit
Pengukuran Luas	Menghitung luas	Proyek, Kooperatif, Remedial	Balok satuan, Kartu gambar, Lembar Kerja	Laporan, Tes, Observasi	45 menit, 60 menit, 75 menit
Pengukuran Volume	Mengukur volume	Proyek, Kooperatif, Remedial	Gelas ukur, Tabung ukur, Lembar Kerja	Laporan, Tes, Observasi	45 menit, 60 menit, 75 menit
Pengukuran Berat	Mengukur berat	Proyek, Kooperatif, Remedial	Timbangan, Neraca, Lembar Kerja	Laporan, Tes, Observasi	45 menit, 60 menit, 75 menit
Pengukuran Waktu	Membaca waktu	Proyek, Kooperatif, Remedial	Jam analog, Jam digital, Lembar Kerja	Laporan, Tes, Observasi	45 menit, 60 menit, 75 menit

Pedoman Penggunaan Media Pembelajaran

Pedoman penggunaan media pembelajaran diberikan kepada guru untuk memastikan media yang tepat digunakan sesuai dengan level kemampuan siswa. Media yang lebih kompleks dan menantang digunakan untuk siswa berkemampuan tinggi, sementara media yang lebih sederhana dan konkret digunakan untuk siswa berkemampuan rendah.

Prinsip-prinsip Pembelajaran Berdiferensiasi

Pembelajaran berdiferensiasi didasarkan pada prinsip-prinsip fleksibilitas, responsivitas, dan keadilan. Pembelajaran didesain untuk mengakomodasi berbagai gaya belajar, tingkat kemampuan, dan minat siswa. Tujuannya adalah untuk memastikan setiap siswa mendapatkan kesempatan belajar yang optimal dan mencapai potensi maksimalnya.

Keunggulan dan Kekurangan Strategi Pembelajaran

Strategi Pembelajaran	Level Kemampuan	Keunggulan	Kekurangan
Pembelajaran Berbasis Proyek	Tinggi	Meningkatkan kemampuan pemecahan masalah dan kreativitas	Membutuhkan waktu yang lebih lama
Pembelajaran Kooperatif	Sedang	Meningkatkan kolaborasi dan komunikasi	Membutuhkan manajemen kelas yang baik
Pembelajaran Remedial Individual	Rendah	Memberikan perhatian individual dan dukungan yang intensif	Membutuhkan waktu dan sumber daya yang lebih banyak

Identifikasi Siswa Berdasarkan Level Kemampuan

Nama Siswa	Level Kemampuan	Justifikasi
[Nama Siswa 1]	Tinggi	Menguasai konsep dengan cepat dan mampu menyelesaikan soal-soal tingkat tinggi
[Nama Siswa 2]	Sedang	Menguasai konsep dengan baik, namun membutuhkan bantuan tambahan untuk soal-soal tingkat tinggi
[Nama Siswa 3]	Rendah	Membutuhkan bantuan yang lebih intensif untuk memahami konsep dasar

Pemilihan Media Pembelajaran yang Tepat

Pemilihan media pembelajaran yang tepat sangat krusial dalam proses belajar mengajar matematika, khususnya di kelas 6 semester 2. Media yang tepat dapat meningkatkan pemahaman siswa, membuat pembelajaran lebih menarik, dan mencapai tujuan pembelajaran secara efektif. Pemilihan ini harus mempertimbangkan berbagai faktor, termasuk karakteristik siswa, materi pelajaran, dan ketersediaan sumber daya.

Nah, kita bicara RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018, bagaimana penyusunannya agar menarik dan efektif? Menariknya, proses perencanaan pembelajaran yang matang juga diterapkan pada jenjang pendidikan yang lebih tinggi, misalnya dalam pengembangan rpp biologi kelas XII kurikulum 2013 revisi 2020 , yang membutuhkan pendekatan berbeda. Kembali ke RPP Matematika kelas 6, perbedaan tingkat kesulitan materi tentu menjadi pertimbangan utama dalam merancang kegiatan pembelajaran yang sesuai dengan kemampuan siswa, bukan?

Jadi, kita perlu melihat bagaimana prinsip-prinsip penyusunan RPP yang baik dapat diterapkan secara konsisten di semua jenjang.

Kriteria Pemilihan Media Pembelajaran Matematika Kelas 6 Semester 2

Kriteria pemilihan media pembelajaran matematika untuk kelas 6 semester 2 berfokus pada kesesuaian dengan materi, tingkat pemahaman siswa, dan keterlibatan siswa dalam proses pembelajaran. Media yang dipilih harus relevan dengan materi bangun ruang yang diajarkan, memiliki tingkat kesulitan yang sesuai dengan kemampuan kognitif siswa kelas 6, dan mampu merangsang minat belajar mereka. Selain itu, pertimbangan praktis seperti ketersediaan, biaya, dan kemudahan penggunaan juga perlu dipertimbangkan.

Media yang interaktif dan memungkinkan siswa untuk berpartisipasi aktif lebih disukai.

Contoh Media Pembelajaran untuk Materi Bangun Ruang

Berbagai media pembelajaran dapat digunakan untuk materi bangun ruang. Salah satu contohnya adalah penggunaan model bangun ruang tiga dimensi, seperti kubus, balok, prisma, dan limas yang terbuat dari bahan yang mudah dijangkau. Siswa dapat secara langsung mengamati bentuk, sisi, rusuk, dan titik sudut dari bangun ruang tersebut. Selain model fisik, media visual seperti gambar, video animasi, atau simulasi komputer juga dapat digunakan untuk memperjelas konsep bangun ruang dan sifat-sifatnya.

Video animasi, misalnya, dapat menunjukkan proses pembentukan bangun ruang secara dinamis, sehingga lebih mudah dipahami oleh siswa. Software edukatif yang memungkinkan siswa untuk memanipulasi model bangun ruang secara virtual juga merupakan pilihan yang efektif.

Perbandingan Berbagai Jenis Media Pembelajaran dan Keunggulannya

Jenis Media	Keunggulan
Model Bangun Ruang 3D	Memungkinkan manipulasi langsung, pengamatan visual yang konkret, dan pemahaman taktil.
Gambar/Ilustrasi	Mudah dipahami, biaya rendah, dan dapat diakses dengan mudah.
Video Animasi	Menampilkan proses dinamis, meningkatkan pemahaman konsep abstrak, dan menarik minat siswa.
Software Edukatif	Interaktif, memungkinkan eksplorasi mandiri, dan menyediakan umpan balik langsung.
Lembar Kerja Interaktif	Meningkatkan partisipasi aktif siswa, menguji pemahaman, dan memberikan latihan terarah.

Penggunaan Media Pembelajaran untuk Meningkatkan Efektivitas Pembelajaran

Penggunaan media pembelajaran yang tepat dapat meningkatkan efektivitas pembelajaran dengan beberapa cara. Media yang dipilih harus mampu memperjelas konsep yang abstrak, membuat pembelajaran lebih menarik dan interaktif, serta memberikan kesempatan bagi siswa untuk berpartisipasi aktif. Integrasi media pembelajaran ke dalam kegiatan pembelajaran harus terencana dengan baik, sehingga dapat mendukung pencapaian tujuan pembelajaran. Guru juga perlu memberikan panduan dan bimbingan kepada siswa dalam menggunakan media pembelajaran tersebut.

Evaluasi berkala terhadap efektivitas penggunaan media pembelajaran juga penting untuk dilakukan.

Rancangan Kegiatan Pembelajaran dengan Berbagai Jenis Media Pembelajaran

Sebagai contoh, pembelajaran tentang volume kubus dapat dimulai dengan demonstrasi model kubus 3D. Siswa kemudian dapat menghitung volume kubus tersebut secara langsung. Selanjutnya, guru dapat menampilkan video animasi yang menunjukkan cara menghitung volume kubus dengan rumus. Setelah itu, siswa dapat mengerjakan lembar kerja interaktif yang berisi soal-soal tentang menghitung volume kubus. Terakhir, siswa dapat menggunakan software edukatif untuk mengeksplorasi konsep volume kubus lebih lanjut dan mengerjakan latihan soal secara mandiri.

Nah, kita bicara soal RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018. Menyusunnya memang butuh ketelitian, menyesuaikan dengan kemampuan siswa. Terkadang, inspirasi juga bisa datang dari sumber tak terduga, misalnya melihat bagaimana struktur buku pelajaran lain disusun. Saya sendiri pernah menemukan struktur bab yang menarik di buku bahasa indonesia kelas 8 kurikulum 2013 revisi 2017 pdf , yang bisa saya adopsi untuk membuat alur pembelajaran Matematika lebih sistematis.

Kembali ke RPP Matematika kelas 6, pengembangan soal-soal latihan pun penting untuk memastikan pemahaman siswa terukur dengan baik.

Dengan menggabungkan berbagai media, pembelajaran akan lebih variatif, menarik, dan efektif.

Penggunaan Soal HOTS (Higher Order Thinking Skills)

Soal HOTS (Higher Order Thinking Skills) dirancang untuk mengukur kemampuan berpikir tingkat tinggi siswa, melampaui pemahaman dan penerapan sederhana. Dalam konteks Kurikulum 2013 revisi 2018, soal HOTS penting untuk memastikan siswa tidak hanya menghafal tetapi juga mampu menganalisis, mengevaluasi, dan menciptakan solusi berdasarkan pemahaman konsep matematika.

Contoh Soal HOTS Materi Pecahan dan Persentase

Berikut lima contoh soal HOTS untuk materi pecahan dan lima contoh soal HOTS untuk materi persentase, masing-masing mencakup minimal satu aspek kognitif dari C4 (Analisis), C5 (Evaluasi), dan C6 (Kreasi) menurut Taksonomi Bloom revisi. Setiap soal disertai kunci jawaban dan pembahasan singkat.

Pecahan:

1. Soal 1 (C4 – Analisis): Ani memiliki 2/3 kg gula dan Budi memiliki 1/2 kg gula. Jika mereka ingin membuat kue yang membutuhkan 1 kg gula, berapa kg gula lagi yang harus mereka beli? Jelaskan langkah-langkah penyelesaiannya.
2. Soal 2 (C5 – Evaluasi): Dua resep kue membutuhkan jumlah tepung yang berbeda. Resep A membutuhkan 3/4 kg tepung, sedangkan resep B membutuhkan 2/3 kg tepung. Manakah resep yang lebih efisien dalam penggunaan tepung? Jelaskan alasanmu.
3. Soal 3 (C6 – Kreasi): Buatlah tiga soal cerita yang berbeda yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian pecahan. Tuliskan juga kunci jawaban untuk setiap soal.
4. Soal 4 (C4 – Analisis): Sebuah lahan berbentuk persegi panjang dengan panjang 2 1/2 meter dan lebar 1 1/3 meter akan ditanami bunga. Berapa luas lahan tersebut? Jelaskan bagaimana kamu menghitung luas lahan yang tidak berbentuk bilangan bulat.
5. Soal 5 (C5 – Evaluasi): Andi memakan 1/4 bagian pizza, Budi memakan 2/8 bagian pizza yang sama. Apakah jumlah pizza yang mereka makan sama? Jelaskan dan buktikan dengan cara menyederhanakan pecahan.

Persentase:

1. Soal 1 (C4 – Analisis): Harga sebuah buku awalnya Rp 50.000,00. Setelah diskon 20%, harga buku tersebut menjadi Rp 40.000,00. Jika toko memberikan diskon tambahan 10% dari harga setelah diskon, berapakah harga akhir buku tersebut? Jelaskan perhitunganmu.
2. Soal 2 (C5 – Evaluasi): Dua toko menawarkan diskon untuk barang yang sama. Toko A menawarkan diskon 30%, sedangkan Toko B menawarkan diskon 20% + 10%. Toko manakah yang menawarkan diskon lebih besar? Jelaskan alasanmu dan hitung selisih diskonnya.
3. Soal 3 (C6 – Kreasi): Buatlah sebuah iklan promosi penjualan yang menawarkan diskon dengan persentase tertentu untuk menarik pelanggan. Sertakan strategi yang digunakan untuk membuat iklan tersebut efektif.
4. Soal 4 (C4 – Analisis): Jumlah siswa kelas 6 adalah 40 siswa. Dari jumlah tersebut, 60% adalah siswa perempuan. Berapa jumlah siswa laki-laki? Jelaskan langkah-langkah perhitungannya.
5. Soal 5 (C5 – Evaluasi): Seorang pedagang membeli barang seharga Rp 100.000,00 dan menjualnya dengan harga Rp 120.000,00. Berapa persentase keuntungan yang diperoleh pedagang tersebut? Jelaskan perhitungan dan analisis keuntungan tersebut.

Kunci Jawaban dan Pembahasan Singkat: (Dihilangkan untuk efisiensi ruang, namun akan dijelaskan secara rinci dalam wawancara selanjutnya)

Merancang Soal HOTS yang Menguji Kemampuan Berpikir Kritis

Merancang soal HOTS yang efektif membutuhkan pertimbangan yang cermat. Soal harus dirancang untuk menguji kemampuan berpikir kritis siswa dalam konteks kehidupan sehari-hari, menggunakan data dan informasi yang relevan. Berikut tiga strategi merancang soal HOTS yang efektif.

1. Mengaitkan dengan Konteks Kehidupan Sehari-hari: Soal-soal harus dikaitkan dengan situasi nyata yang mudah dipahami siswa. Misalnya, soal tentang menghitung persentase diskon di supermarket atau menghitung pecahan dalam resep masakan.
2. Menggunakan Data dan Informasi yang Relevan: Soal-soal harus dilengkapi dengan data dan informasi yang relevan dan akurat. Data tersebut harus cukup untuk menantang siswa dalam menganalisis dan mengevaluasi informasi.
3. Memvariasikan Jenis Soal: Gunakan berbagai jenis soal, seperti soal uraian, esai, atau pemecahan masalah, untuk menguji berbagai aspek kemampuan berpikir siswa.

Kisi-kisi Soal HOTS Materi Pecahan dan Persentase

Kisi-kisi soal HOTS berikut mencakup berbagai aspek kognitif (C4, C5, dan C6) untuk materi pecahan dan persentase. Kisi-kisi ini menunjukkan indikator pencapaian kompetensi, jenis soal (uraian atau esai), dan bobot nilai untuk masing-masing soal.

Indikator	Jenis Soal	Aspek Kognitif	Bobot Nilai
Menentukan luas bangun datar dengan ukuran pecahan	Uraian	C4	15
Menganalisis perbandingan dua pecahan	Uraian	C4	15
Mengevaluasi efisiensi penggunaan bahan berdasarkan pecahan	Esai	C5	20
Menghitung persentase keuntungan/kerugian	Uraian	C4	15
Membandingkan dua penawaran diskon yang berbeda	Esai	C5	20
Merancang strategi pemasaran yang melibatkan persentase diskon	Esai	C6	15

Tingkat Kesulitan Soal HOTS

Tingkat kesulitan soal HOTS dapat diklasifikasikan berdasarkan aspek kognitif (C4, C5, dan C6). Berikut tabel yang menunjukkan tingkat kesulitan soal HOTS untuk setiap materi (pecahan dan persentase).

Materi	Aspek Kognitif	Tingkat Kesulitan	Deskripsi Indikator
Pecahan	C4 (Analisis)	Sedang	Membutuhkan kemampuan untuk membandingkan dan mengklasifikasikan informasi yang diberikan.
Pecahan	C5 (Evaluasi)	Sukar	Membutuhkan kemampuan untuk menilai dan membuat keputusan berdasarkan informasi yang kompleks.
Pecahan	C6 (Kreasi)	Sukar	Membutuhkan kemampuan untuk menghasilkan ide-ide baru dan solusi yang orisinal.
Persentase	C4 (Analisis)	Sedang	Membutuhkan kemampuan untuk memecah masalah menjadi bagian-bagian yang lebih kecil dan mengidentifikasi hubungan antar bagian.
Persentase	C5 (Evaluasi)	Sukar	Membutuhkan kemampuan untuk membuat pertimbangan nilai dan memilih solusi terbaik berdasarkan kriteria tertentu.
Persentase	C6 (Kreasi)	Sukar	Membutuhkan kemampuan untuk mengembangkan solusi yang inovatif dan kreatif.

Menganalisis Jawaban Siswa pada Soal HOTS

Menganalisis jawaban siswa pada soal HOTS harus memperhatikan proses berpikir siswa, bukan hanya hasil akhir. Hal ini penting untuk mengidentifikasi kekuatan dan kelemahan berpikir siswa, sehingga dapat diberikan bimbingan yang tepat.

(Contoh analisis jawaban siswa untuk satu soal HOTS tertentu akan dijelaskan secara rinci dalam wawancara selanjutnya)

Mengembangkan Kemampuan Pemecahan Masalah

Kemampuan pemecahan masalah merupakan kompetensi penting yang harus dimiliki siswa, tak hanya dalam matematika, tetapi juga dalam kehidupan sehari-hari. Dalam konteks pembelajaran matematika kelas 6 semester 2, pengembangan kemampuan ini sangat krusial untuk membantu siswa menerapkan konsep matematika dalam situasi nyata dan menyelesaikan permasalahan yang kompleks. Wawancara berikut akan membahas bagaimana hal ini dapat dicapai.

RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018 memang menuntut persiapan matang. Tantangannya, bagaimana memastikan materi tersampaikan efektif dan menarik bagi siswa? Nah, untuk membantu proses penyusunan RPP yang berkualitas, kita bisa memanfaatkan berbagai sumber referensi, bahkan mencari inspirasi desain pembelajaran yang inovatif lewat platform seperti Identif.id , yang menawarkan berbagai solusi edukatif.

Kembali ke RPP, perencanaan yang terstruktur dan sesuai dengan karakteristik siswa akan sangat menentukan keberhasilan proses belajar mengajar. Dengan demikian, tujuan pembelajaran pun dapat tercapai secara optimal.

Contoh Soal Cerita yang Menguji Kemampuan Pemecahan Masalah

Soal cerita yang efektif dirancang untuk menantang siswa memahami masalah, mengidentifikasi informasi penting, dan menerapkan strategi pemecahan masalah yang tepat. Berikut contohnya:

“Bu Ani memiliki 3 keranjang apel. Keranjang pertama berisi 25 apel, keranjang kedua berisi 32 apel, dan keranjang ketiga berisi 28 apel. Bu Ani ingin membagi apel tersebut sama banyak ke dalam 5 kantong plastik. Berapa banyak apel yang ada di setiap kantong plastik?”

RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018 memang menuntut persiapan yang matang, bukan hanya soal penguasaan materi, tetapi juga metode penyampaian yang efektif. Menariknya, persiapan yang sistematis juga dibutuhkan untuk mata pelajaran lain, misalnya bagaimana kita menyusun RPP yang berkualitas untuk PAI, seperti yang bisa kita lihat contohnya di rpp pai kelas 8 semester 1 kurikulum 2013.

Pengalaman merancang RPP PAI yang efektif ini, bisa memberikan inspirasi untuk menyempurnakan RPP Matematika kita, menciptakan pembelajaran yang lebih bermakna bagi siswa. Kembali ke RPP Matematika kelas 6, perlu diingat bahwa pemahaman konsep dan keterampilan pemecahan masalah merupakan kunci keberhasilan pembelajaran.

Langkah-langkah Pemecahan Masalah Matematika

Siswa perlu memahami alur berpikir sistematis dalam menyelesaikan soal matematika. Berikut langkah-langkah yang dapat diterapkan:

1. Memahami masalah: Identifikasi apa yang diketahui dan apa yang ditanyakan dalam soal.
2. Merencanakan penyelesaian: Tentukan strategi atau rumus yang tepat untuk menyelesaikan masalah.
3. Melaksanakan rencana: Kerjakan perhitungan sesuai dengan rencana yang telah dibuat.
4. Memeriksa kembali jawaban: Pastikan jawaban masuk akal dan sesuai dengan konteks soal.

Aktivitas Pembelajaran untuk Meningkatkan Kemampuan Pemecahan Masalah

Berbagai aktivitas pembelajaran dapat dirancang untuk meningkatkan kemampuan pemecahan masalah siswa secara aktif dan menyenangkan. Beberapa contohnya:

• Pembelajaran berbasis masalah (Problem-Based Learning): Siswa dihadapkan pada masalah nyata yang menantang mereka untuk menemukan solusi menggunakan konsep matematika yang telah dipelajari. Contohnya, menghitung biaya perjalanan wisata kelas dengan mempertimbangkan berbagai faktor seperti transportasi, akomodasi, dan tiket masuk.
• Game dan simulasi: Game edukatif dan simulasi dapat memberikan pengalaman interaktif dan menyenangkan dalam memecahkan masalah matematika. Contohnya, permainan strategi yang melibatkan perhitungan dan pengambilan keputusan.
• Diskusi kelompok: Diskusi kelompok memungkinkan siswa bertukar ide dan strategi dalam menyelesaikan masalah, sehingga dapat memperkaya pemahaman mereka.

Rubrik Penilaian Kemampuan Pemecahan Masalah

Rubrik penilaian membantu guru mengukur kemampuan pemecahan masalah siswa secara objektif dan terstruktur. Rubrik ini akan menilai aspek pemahaman masalah, perencanaan penyelesaian, pelaksanaan, dan pengecekan jawaban.

Aspek	Sangat Baik (4)	Baik (3)	Cukup (2)	Kurang (1)
Memahami Masalah	Memahami masalah dengan sangat baik dan mampu mengidentifikasi semua informasi penting.	Memahami masalah dengan baik dan mampu mengidentifikasi sebagian besar informasi penting.	Memahami masalah dengan cukup baik, tetapi masih ada beberapa informasi penting yang terlewatkan.	Tidak memahami masalah dengan baik dan kesulitan mengidentifikasi informasi penting.
Merencanakan Penyelesaian	Merencanakan penyelesaian dengan strategi yang tepat dan efisien.	Merencanakan penyelesaian dengan strategi yang cukup tepat, tetapi masih bisa ditingkatkan.	Merencanakan penyelesaian dengan strategi yang kurang tepat, sehingga proses penyelesaian menjadi kurang efisien.	Tidak mampu merencanakan penyelesaian dengan strategi yang tepat.
Melaksanakan Rencana	Melaksanakan rencana dengan tepat dan akurat.	Melaksanakan rencana dengan cukup tepat, tetapi terdapat beberapa kesalahan kecil.	Melaksanakan rencana dengan beberapa kesalahan yang cukup signifikan.	Tidak mampu melaksanakan rencana dengan benar.
Memeriksa Kembali Jawaban	Memeriksa kembali jawaban dengan teliti dan mampu mengidentifikasi kesalahan jika ada.	Memeriksa kembali jawaban, tetapi masih ada beberapa kesalahan yang terlewatkan.	Kurang teliti dalam memeriksa kembali jawaban, sehingga beberapa kesalahan tidak terdeteksi.	Tidak memeriksa kembali jawaban.

Indikator Kemampuan Pemecahan Masalah dan Contoh Pertanyaan

Indikator kemampuan pemecahan masalah dapat diukur melalui berbagai pertanyaan yang dirancang untuk menguji kemampuan siswa dalam setiap tahapan proses pemecahan masalah.

Indikator	Contoh Pertanyaan
Mampu memahami masalah	Apa yang diketahui dan ditanyakan dalam soal cerita tersebut?
Mampu merencanakan penyelesaian	Strategi apa yang akan kamu gunakan untuk menyelesaikan masalah ini? Jelaskan alasannya.
Mampu melaksanakan rencana	Tunjukkan langkah-langkah perhitunganmu secara detail.
Mampu memeriksa kembali jawaban	Apakah jawabanmu masuk akal? Bagaimana kamu mengecek kebenaran jawabanmu?

Menyusun Laporan Pembelajaran

Laporan pembelajaran merupakan instrumen penting bagi guru untuk merefleksikan praktik pembelajaran, mengidentifikasi area yang perlu diperbaiki, dan meningkatkan efektivitas pengajaran. Laporan ini tidak hanya berisi data kuantitatif, tetapi juga informasi kualitatif yang memberikan gambaran menyeluruh tentang proses dan hasil pembelajaran.

Contoh Laporan Pembelajaran Matematika Kelas 5 SD Tema “Pecahan”

Berikut contoh laporan pembelajaran Matematika kelas 5 SD dengan tema “Pecahan” yang mencakup perencanaan, pelaksanaan, dan hasil pembelajaran. Laporan ini menggunakan data fiktif untuk ilustrasi.

Perencanaan Pembelajaran

• Tujuan Pembelajaran: Siswa mampu memahami konsep pecahan biasa, desimal, dan campuran; serta mampu melakukan operasi hitung sederhana pada pecahan.
• Metode Pembelajaran: Ceramah, diskusi kelompok, permainan edukatif, dan penugasan individu.
• Media Pembelajaran: Kartu pecahan, gambar, video edukatif, dan buku teks.
• Penilaian: Tes tertulis, observasi partisipasi siswa dalam diskusi, dan penilaian portofolio pekerjaan siswa.

Pelaksanaan Pembelajaran

Pembelajaran berlangsung selama 6 pertemuan, setiap pertemuan berdurasi 60 menit. Kegiatan pembelajaran meliputi penjelasan konsep, diskusi kelompok untuk memecahkan soal, permainan edukatif untuk meningkatkan pemahaman, dan pemberian tugas individu.

• Deskripsi Kegiatan: Siswa aktif berpartisipasi dalam diskusi dan permainan. Beberapa siswa menunjukkan kesulitan dalam memahami konsep pecahan campuran.
• Kendala yang Dihadapi: Beberapa siswa kesulitan memahami konsep pecahan campuran dan operasi hitung pecahan. Beberapa siswa kurang fokus selama pembelajaran.
• Solusi: Pemberian bimbingan individual kepada siswa yang mengalami kesulitan, penggunaan media pembelajaran yang lebih interaktif seperti video edukatif, dan modifikasi metode pembelajaran agar lebih menarik.

Hasil Pembelajaran

Data kuantitatif dan kualitatif dikumpulkan untuk menganalisis hasil pembelajaran. Data kuantitatif berupa nilai ulangan harian siswa, sedangkan data kualitatif berupa catatan lapangan dan observasi selama proses pembelajaran.

Topik	Jumlah Siswa	Nilai Rata-rata	Persentase Siswa di atas KKM (70)	Keterangan
Pecahan Biasa	30	75	80%	Sebagian besar siswa mampu memahami konsep pecahan biasa.
Pecahan Desimal	30	72	70%	Pemahaman siswa terhadap pecahan desimal cukup baik.
Pecahan Campuran	30	68	50%	Siswa masih mengalami kesulitan dalam memahami konsep pecahan campuran.

Berdasarkan data di atas, terlihat bahwa pemahaman siswa terhadap pecahan biasa dan desimal relatif baik, sedangkan pemahaman terhadap pecahan campuran masih perlu ditingkatkan. Catatan lapangan menunjukkan beberapa siswa masih kesulitan dalam mengubah pecahan biasa ke desimal dan sebaliknya.

Analisis Data Hasil Pembelajaran dan Saran Perbaikan

Analisis data nilai ulangan harian siswa (data CSV terlampir) menunjukkan kekuatan dan kelemahan pembelajaran. Kekuatannya adalah sebagian besar siswa mampu memahami pecahan biasa dan desimal. Kelemahannya adalah pemahaman siswa terhadap pecahan campuran masih rendah. Saran perbaikan meliputi peningkatan penggunaan media visual interaktif sebesar 20% pada pertemuan selanjutnya, serta pemberian latihan soal yang lebih variatif dan terfokus pada pecahan campuran.

Evaluasi Efektivitas Pembelajaran

Berdasarkan laporan pembelajaran, terlihat bahwa tujuan pembelajaran sebagian besar tercapai, terutama pada materi pecahan biasa dan desimal. Namun, perlu dilakukan perbaikan pada pembelajaran pecahan campuran untuk meningkatkan pemahaman siswa. Rekomendasi untuk pembelajaran selanjutnya adalah penggunaan metode pembelajaran yang lebih variatif dan media pembelajaran yang lebih interaktif untuk meningkatkan pemahaman siswa terhadap pecahan campuran.

Refleksi Pribadi

Pembelajaran pecahan ini memberikan tantangan tersendiri, terutama dalam mengatasi kesulitan siswa dalam memahami pecahan campuran. Saya belajar pentingnya memberikan bimbingan individual dan menggunakan media pembelajaran yang lebih bervariasi. Penggunaan game edukatif terbukti efektif meningkatkan antusiasme siswa. Ke depannya, saya akan lebih fokus pada strategi pembelajaran yang mengakomodasi perbedaan kemampuan belajar siswa.

Membahas RPP Matematika kelas 6 semester 2 Kurikulum 2013 revisi 2018, kita perlu melihat bagaimana penyusunannya bisa lebih efisien. Perbedaannya dengan RPP jenjang pendidikan dasar lainnya cukup signifikan, misalnya, jika kita bandingkan dengan kemudahan RPP satu lembar untuk kelas 1 semester 2 seperti yang bisa dilihat di rpp 1 lembar kelas 1 semester 2 , maka RPP Matematika kelas 6 akan lebih detail dan kompleks mengingat materi yang jauh lebih luas.

Namun, prinsip-prinsip pembelajaran yang efektif tetap harus diintegrasikan dalam RPP kelas 6 tersebut, mengingat pentingnya pemahaman konseptual bagi siswa di usia tersebut.

Simpulan Akhir

Memahami dan mengaplikasikan RPP Matematika Kelas 6 Semester 2 Kurikulum 2013 Revisi 2018 bukan hanya tugas guru, tetapi juga investasi jangka panjang bagi keberhasilan siswa. Dengan perencanaan yang tepat, metode yang variatif, dan evaluasi yang komprehensif, RPP ini menjadi alat yang ampuh untuk membentuk generasi yang cakap dalam matematika dan siap menghadapi tantangan masa depan. Semoga pemaparan ini memberikan gambaran yang komprehensif dan menginspirasi guru untuk menciptakan pembelajaran matematika yang efektif dan bermakna.

Panduan Tanya Jawab

Apakah RPP ini bisa diadaptasi untuk kelas akselerasi?

Ya, RPP ini dapat diadaptasi. Tingkat kesulitan soal dan materi dapat ditingkatkan sesuai kemampuan siswa akselerasi.

Bagaimana cara mengatasi siswa yang kesulitan memahami konsep pecahan?

Gunakan media konkret seperti potongan kue atau gambar, serta metode pembelajaran yang variatif dan berulang.

Sumber daya apa saja yang dibutuhkan selain buku teks?

Alat peraga matematika (kubus, balok, penggaris), kartu soal, internet untuk akses sumber belajar online.

Bagaimana cara mengukur pemahaman konsep bangun ruang secara efektif?

Gunakan kombinasi tes tertulis, praktikum membuat bangun ruang, dan presentasi hasil kerja kelompok.